Тотожні перетворення виразів які містять квадратні корені

Квадратична функція і її графік

Цілі:

• развить умение обобщать и систематизировать изученный материал;
• рассмотреть построение графика функции y = x² и её свойства, используя график функции y = x², научиться находить значение функции и значения аргумента, развивать графическую грамотность.

ХІД УРОКУ

I. Организационный момент.

II. Повторение. Работа по учебнику.

Вспоминаем, что с графиками линейной функции уже знакомились в этом учебном году.

Задание по рядам:

• 1-й ряд: п.10 підр. Дать определение функциональной зависимости или функции; зависимой и независимой переменной.
  Пусть функция задана формулой y = 2x + 1. Найти значение y, если x = 0; 1; –3
• 2-й ряд: п.13,14 учебника. Дать определение линейной функции. Графики функции y = kx + b; y = kx; y = k.
• 3-й ряд: Не выполняя построение, выясните, проходит ли график функции, заданной формулой y = 1,25x – 5 через точку
  A(12; 10); K(–20; –30); C(16; –15).

После того как каждый ряд получил задание, идёт обсуждение его, обобщение и систематизация изученного материала, поиск решения задачи, затем один из представителей от ряда выступает у доски для всего класса.

III. Изучение нового материала.

Была рассмотрена линейная функция.

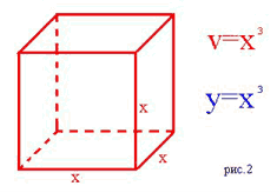
Но возникает вопрос: а не существует ли зависимость одной переменной y от другой переменной x, но заданная не формулой y = kx + b, а как-то иначе? Конечно, существует. Если, например, x – сторона квадрата, а y – его площадь, то y = x² (рис.1). Если x – сторона куба, а y – его объём, то
y = x³ (рис.2). На этом уроке мы рассмотрим функцию y = x² и построим её график.

IV. Работа с електронною  програмою

Побудова графіка зав допомогою програми ADVANCHED GRAPHER/

V. Работа в тетрадях и на доске:

Задание: построить график функции y = x²

В ходе построения графика и объяснение учителем новых понятий, записывается словарь:

• Квадратичная функция
• Парабола
• Ветви параболы
• Вершина параболы
• Ось симметрии параболы

По графику функции y = x² учащиеся выясняют свойства функции:

1. Если х = 0, то у = 0
2. Если х <> 0, то y > 0
3. Ось ОХ – ось симметрии

Творческое задание для сильных учеников: исследовать поведение функции y = kx²

• 1-я гр. (2–3 чел.). Построить график функции y = –x²
• 2-я гр. (2 чел.). Построить график функции y = 5x²
• 3-я гр. Построить график функции 1/2 x²

Задания выполняют фломастерами на отдельных листах, затем представители от группы выступает перед классом.

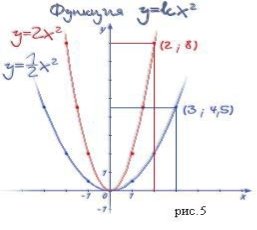
Делается вывод: существует ещё целый класс функций, графики которых называют параболами. Это класс квадратичных функций. Поведение их графиков зависит от коэффициента k.

Подтверждение по электронному учебнику (рис.5).

В это время остальные учащиеся выполняют задания:

1. принадлежит ли графику функции y = x² точка A(–5; 25), B(1/4; –1/16), C(0,6; –0,36);
2.          (из учебника).

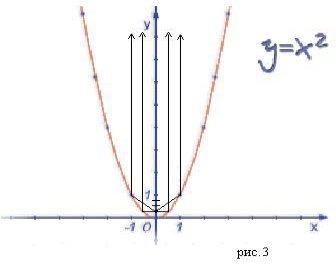
В заключение отметим одно любопытное свойство параболы, открытое и доказанное физиками и математиками.

Сообщение: Если рассматривать параболу y = x² как экран, как отражающую поверхность, а в точке (0; 1/4) поместить источник света, то лучи, отражаясь от параболы-экрана, образуют параллельный пучок света (рис.3). Точку (0; 1/4) называют фокусом параболы. Эта идея используется в автомобилях: отражающая поверхность фары имеет параболическую форму, а лампочку помещают в фокусе – тогда свет от фары распространяется достаточно далеко.

VI. Задание на дом:

VII. Итог урока. Рефлексия.

Учащиеся отвечают на любой из вопросов или заканчивают фразу:

Наш урок подошёл к концу, и я хочу сказать…

• мне больше всего удалось…
• меня особенно удивило…
• для меня было открытием то, что …
• за что ты можешь себя похвалить?
• за что ты можешь похвалить одноклассников?
• за что ты можешь похвалить учителя?
• что на ваш взгляд удалось?
• что на ваш взгляд не удалось? Почему? Что учесть на будущее?
• мои достижения на уроке.