Тотожність корінь квадратний а^2 = a . Рівняння х2 = а

Про матеріал

: сформувати в учнів знання про тотожність та , вміння застосовувати вивчену властивість для обчислення значень числових виразів, що містять арифметичний квадратний корінь з числа, а також перетворення буквених виразів; розвивати увагу, логічне мислення, пам’ять; виховувати акуратність, працелюбність, дисциплінованість.

Перегляд файлу

Урок № 37 ________________ 8 кл.(алгебра)

Тема уроку:Тотожність . Рівняння х² = а

Мета уроку: сформувати в учнів знання про тотожність та , вміння застосовувати вивчену властивість для обчислення значень числових виразів, що містять арифметичний квадратний корінь з числа, а також перетворення буквених виразів; розвивати увагу, логічне мислення, пам’ять; виховувати акуратність, працелюбність, дисциплінованість.

Тип уроку: урок засвоєння нових знань.

Обладнання: підручник, роздавальний матеріал,

I. Організаційний етап

▪ Привітання

▪ Перевірка присутності учнів

▪ Перевірка готовності учнів та кабінету до уроку

II. Перевірка домашнього завдання

▪ Перевірка письмового завдання біля дошки

▪ Графічний диктант (так , ні __)

Чи є правильним твердження, що:

1) кожне натуральне число є цілим;

2) будь-яке ірраціональне число є дійсним;

3) будь-яке дійсне число є раціональним;

4) — ірраціональне число;

5) — ірраціональне число;

6) — раціональне число?

Запропонувати учням здійснити самоперевірку за ключем-відповіддю, заздалегідь підготовленим на відкидній дошці.

III. Формулювання мети й завдань уроку, мотивація навчальної діяльності

▪ Оголошення теми уроку

▪ Формулювання разом з учнями мети й завдань уроку

▪ Мотивація навчальної діяльності

Знайдемо значення виразу . Це нескладно зробити, і, як ви розумієте, отримаємо . Знайдіть значення виразів , , .

IV. Актуалізація опорних знань

▪ Бліц-опитування за технологією «Мікрофон»

1. Обчисліть:

а) ; б) ; в) ;

2. Піднесіть до квадрата:

а) 5; б) –3; в) ; г) 0,4.

V. Засвоєння нових знань

План викладання нового матеріалу

Тотожність .
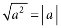Рівняння х² = а

Тотожність та

Доведемо, що за будь-якого значення a виконується рівність .

Доведення

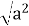=|a | при будь-якому дійсному числу а має зміст :

= a, якщо a ; = - a , якщо а < 0 .

2) , якщо a , то

і , якщо , то і . Отже, рівність є правильною.

Наприклад, ; .

= =|| = = 49;

= =|| = = 49 ( за властивістю степеня з парним показником)

Приклад. Спростіть вираз , якщо а 0, b 0 .

Розв’язання

Дослідження кількості коренів рівняння графічним способом.

Розгляньмо рисунок, на якому зображено параболу і пряму .

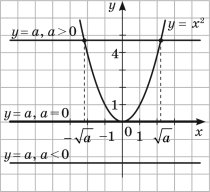
37_этап 5

Розглянемо випадки, якщо ; ; .

Якщо , то пряма перетинає параболу у двох точках з абсцисами і . Отже, в цьому випадку рівняння має два корені.

Якщо , то маємо пряму . З параболою в неї одна спільна точка . Отже, в цьому випадку рівняння має один корінь.

Якщо , то пряма не перетинає параболу. Отже, в цьому випадку рівняння коренів не має.

Наприклад, рівняння має два корені: 3 і –3, а рівняння коренів не має.

2. Розв’язання рівняння .

Ми вже побачили, розв’язуючи графічно рівняння , що якщо , то рівняння має корені, а якщо , то коренями рівняння є числа і .

Доведемо це.

1. Оскільки — правильна рівність, то — корінь рівняння .

2. — правильна рівність, тоді — корінь рівняння .

Якщо , то . Наприклад, рівняння має два корені: і . Якщо , то рівняння коренів не має. Отже, розглянемо схему.

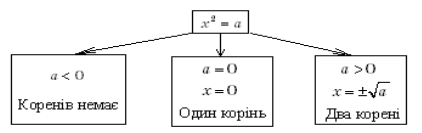
3. Висновок про існування арифметичного квадратного кореня з невід’ємного числа.

Зауважимо, що до поняття квадратного кореня ми дійшли, розв’язуючи рівняння , де . Корені цього рівняння — числа, кожне з яких є квадратним коренем з числа a. Графічно ми переконалися, що коли відоме a , то ми завжди знайдемо відповідне значення x.