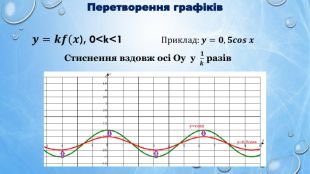
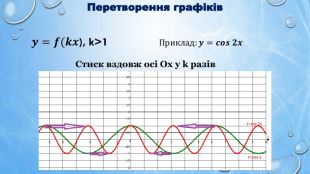
Тригонометрична функція. Повторення
Про матеріал
Повторення матеріалу з теми "Тригонометрична функція" у 11 класі. Містить завдання ЗНО/НМТ минулих років. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



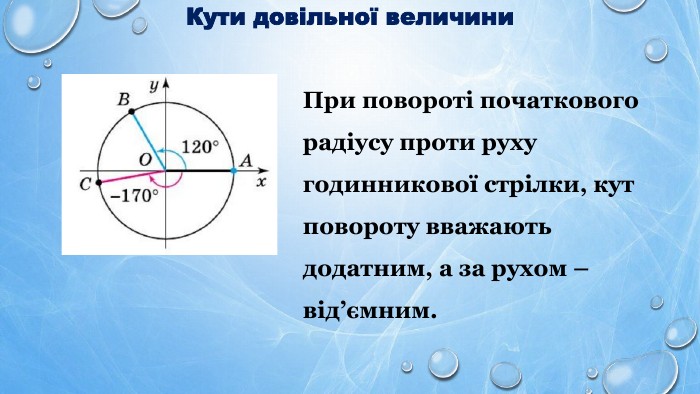

![Функція sin x (період 2π){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіsinx >0 при (2πn; π+2πn) n Є Zsinx <0 при (2πn; π+2πn) n Є ZПарність. Непарна. Зростання/Спадання. Зростає на кожному з проміжків виду [- π2+2πn;π2+2πn] n Є ZСпадає на кожному з проміжків виду [π2+2πn;3π2+2πn] n Є ZНайбільше і найменше значення(екстремуми)Найбільшого значення,яке дорівнює 1,набуває в точках видуπ2+2πn; n Є ZНайменшого значення,яке дорівнює -1,набуває в точках виду - π2+2πn; n Є Z{6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіsinx >0 при (2πn; π+2πn) n Є Zsinx <0 при (2πn; π+2πn) n Є ZПарність. Непарна. Зростання/Спадання. Найбільше і найменше значення(екстремуми) Функція sin x (період 2π){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіsinx >0 при (2πn; π+2πn) n Є Zsinx <0 при (2πn; π+2πn) n Є ZПарність. Непарна. Зростання/Спадання. Зростає на кожному з проміжків виду [- π2+2πn;π2+2πn] n Є ZСпадає на кожному з проміжків виду [π2+2πn;3π2+2πn] n Є ZНайбільше і найменше значення(екстремуми)Найбільшого значення,яке дорівнює 1,набуває в точках видуπ2+2πn; n Є ZНайменшого значення,яке дорівнює -1,набуває в точках виду - π2+2πn; n Є Z{6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіsinx >0 при (2πn; π+2πn) n Є Zsinx <0 при (2πn; π+2πn) n Є ZПарність. Непарна. Зростання/Спадання. Найбільше і найменше значення(екстремуми)](/uploads/files/604010/349059/401110_images/6.jpg)
![Функція cos x (період 2π){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіcosx >0 при (- π2+2πn;π2+2πn) n Є Zcosx <0 при (π2+2πn;3π2+2πn) n Є ZПарність. Парна cos(-x) = cosx. Зростання/Спадання. Зростає на кожному з проміжків виду [π+2πn; 2π+2πn] n Є ZСпадає на кожному з проміжків виду [2πn; π+2πn] n Є ZНайбільше і найменше значення(екстремуми)Найбільшого значення,яке дорівнює 1,набуває в точках виду2πn; n Є ZНайменшого значення,яке дорівнює -1,набуває в точках виду π+2πn; n Є Z{6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіПарність. Парна cos(-x) = cosx. Зростання/Спадання. Зростає на кожному з проміжків виду [π+2πn; 2π+2πn] n Є ZСпадає на кожному з проміжків виду [2πn; π+2πn] n Є ZНайбільше і найменше значення(екстремуми) Функція cos x (період 2π){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіcosx >0 при (- π2+2πn;π2+2πn) n Є Zcosx <0 при (π2+2πn;3π2+2πn) n Є ZПарність. Парна cos(-x) = cosx. Зростання/Спадання. Зростає на кожному з проміжків виду [π+2πn; 2π+2πn] n Є ZСпадає на кожному з проміжків виду [2πn; π+2πn] n Є ZНайбільше і найменше значення(екстремуми)Найбільшого значення,яке дорівнює 1,набуває в точках виду2πn; n Є ZНайменшого значення,яке дорівнює -1,набуває в точках виду π+2πn; n Є Z{6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. RОбласть значень[-1; 1]Періодичність. Періодична з головним періодом,який дорівнює 2πПроміжки знакосталостіПарність. Парна cos(-x) = cosx. Зростання/Спадання. Зростає на кожному з проміжків виду [π+2πn; 2π+2πn] n Є ZСпадає на кожному з проміжків виду [2πn; π+2πn] n Є ZНайбільше і найменше значення(екстремуми)](/uploads/files/604010/349059/401110_images/7.jpg)
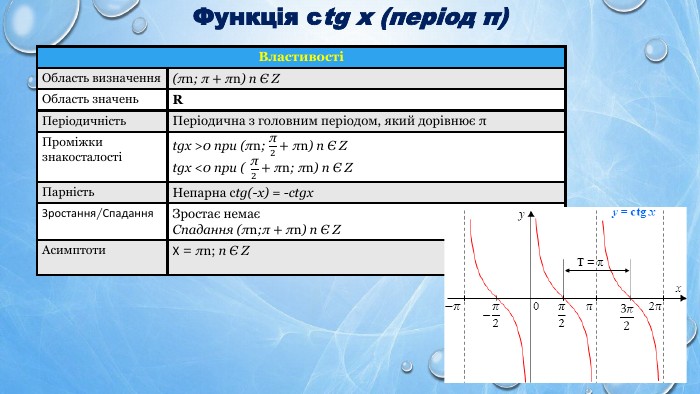
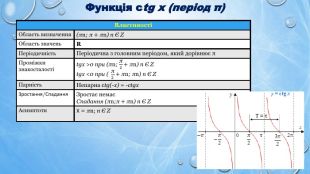
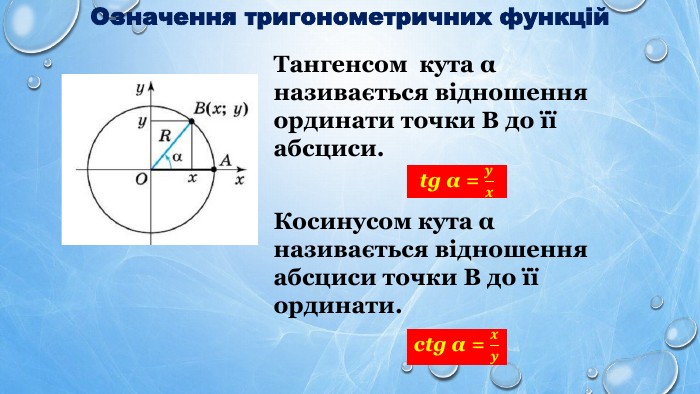
![Функція tg x (період π){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення(- π2+πn;π2+πn) n Є ZОбласть значень. RПеріодичність. Періодична з головним періодом,який дорівнює πПроміжки знакосталостіtgx >0 при (πn; π2+πn) n Є Ztgx <0 при (- π2+πn; πn) n Є ZПарність. Непарна tg(-x) = -tgx. Зростання/Спадання. Зростає на кожному з проміжків виду [- π2+πn;π2+πn] n Є ZСпадає немаєАсимптоти. Х = π2+πn; n Є ZТочки перетину з осями. Ох: (πn;0) n Є ZОу: (0; 0){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. Область значень. RПеріодичність. Періодична з головним періодом,який дорівнює πПроміжки знакосталостіПарність. Непарна tg(-x) = -tgx. Зростання/Спадання. Асимптоти. Точки перетину з осями Функція tg x (період π){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення(- π2+πn;π2+πn) n Є ZОбласть значень. RПеріодичність. Періодична з головним періодом,який дорівнює πПроміжки знакосталостіtgx >0 при (πn; π2+πn) n Є Ztgx <0 при (- π2+πn; πn) n Є ZПарність. Непарна tg(-x) = -tgx. Зростання/Спадання. Зростає на кожному з проміжків виду [- π2+πn;π2+πn] n Є ZСпадає немаєАсимптоти. Х = π2+πn; n Є ZТочки перетину з осями. Ох: (πn;0) n Є ZОу: (0; 0){6 E25 E649-3 F16-4 E02-A733-19 D2 CDBF48 F0}ВластивостіОбласть визначення. Область значень. RПеріодичність. Періодична з головним періодом,який дорівнює πПроміжки знакосталостіПарність. Непарна tg(-x) = -tgx. Зростання/Спадання. Асимптоти. Точки перетину з осями](/uploads/files/604010/349059/401110_images/8.jpg)