Урок "Геометрична прогресія. Знаходження суми п перших членів геометричної прогресії"

Комісарівська ЗОШ І-ІІІ ступенів

 

 

 

 

 

Геометрична прогресія.

Знаходження суми п перших членів геометричної прогресії

 

 

 

Відкритий урок у 9 класі

 

 

 

Вчитель: Бережна Т.В

 

 

 

 

 

2023р.

Тема уроку: Знаходження суми п перших членів геометричної прогресії

 

Мета уроку: вивести формулу знаходження суми п перших членів геометричної прогресії, показати її практичне застосування, розв’язувати вправи на застосування цієї формули.

                        розвивати уміння застосовувати формули при розв’язуванні задач, раціонально виконувати обчислення,

                        виховувати любов до математики, культуру мовлення.

 

Обладнання: роздатковий матеріал.

 

 

Хід уроку

 

Організаційний момент

Використовуючи форму «мікрофон», повторити вивчений матеріал, відповівши на питання:

• Дати означення геометричної прогресії
• Що називають знаменником геометричної прогресії ?
• Як обчислити п-й член геометричної прогресії?
• Як визначити з цієї формули в₁?, q ?
• Дати історичну довідку поняття геометричної прогресії
• Яку властивість має кожний член геометричної прогресії, починаючи з другого?

 

 

1. в₁ = 3;     в₂ =6.       Знайти: q.

2. в₁ =5,      q = -4       Знайти: в₂.

3. в₁ = -2;  q =3.         Знайти: в₄.

4. в ₅= 80;    q= -2;      Знайти: в₁.

5. в₁ = 3;    в₃ =48;    Знайти:в₂.

 

Відповіді записати в таблицю і відгадати зашифроване слово

 

1	2	3	4	5

 

 

Шифр:

 

10	-20	-0,06	320	-54	2	5	11	12	28	-40
А	Ю	Р	Я	Б	Л	О	Е	В	М	Г

 

Мотивація:

У слові «прогресія» коренем є слово «прогрес», що з латини означає «крок вперед». Отже, тема спонукає нас зробити крок уперед, досягти прогресу. Ми знаємо, чого хочемо досягти, але навіщо нам це потрібно, навіщо вивчається ця тема? Прогресії є відображенням світу, що нас оточує. Застосовуються прогресії у фізиці під час вивчення тіл, що вільно падають чи рухаються рівноприскорено, та під час вивчення процесу радіактивного розпаду елементів та атомів. Також у економіці та банківській справі, під час виплати відсотків та надання кредитів. Прогресії є у техніці під час виготовлення обладнання.

Послухаємо доповідь учня про прогресії у житті. (Додаток А)

 

 

 

Пояснення нового матеріалу:

 

Пояснення нового матеріалу почнемо з стародавньої легенди.

Шахи – одна із самих древніх ігор, була придумана в Індії. Коли індуський цар Шерам познайомився з нею, він був у захваті від її оригінальності. Узнавши, що вона була винайдена одним із його підданих, цар приказав його привести, щоб особисто нагородити за вдалу видумку.

 Винахідник, його звали Сета, з’явився до трону повелителя. Це був скромно одітий вчений, який заробляв на життя, навчаючи своїх учнів.

•      Я достатньо багатий, щоб виконати саме сміливе твоє бажання, - сказав цар. - Назви нагороду, яка тебе задовольнить, і ти отримаєш її.

 Сета,  подумавши, сказав: прикажи видати мені за першу клітинку шахової дошки одну пшеничну зернину.

• Просту пшеничну зернину? –перепитав цар.
• Так, повелителю. За другу клітинку прикажи видати 2 зернини, за третю – 4, за четверту -8….
•      Достатньо, сердито перервав його цар. - Ти одержиш свої зернини за всі 64 клітини дошки відповідно до твого бажання: за кожну наступну вдвічі більше від попередньої. Але знай, що твоя просьба недостойна моєї щедрості. Як учитель, ти міг би показати кращий приклад поваги до свого повелителя. Іди. Слуги мої винесуть тобі твій мішок з пшеницею.

        Сета посміхнувся і залишив залу.

        Вранці царю доповіли, що старшина придворних математиків просить вислухати важливе донесення.

•      Ми добросовісно цілу ніч рахували всю кількість зернин, які бажає одержати Сета. Це число дуже велике і не у твоїй владі, повелителю, виконати подібне бажання. Не знайдеться такої кількості зерна на всіх просторах планети Земля. І якщо бажаєш видати обіцяну нагороду, то прикажи перетворити всі царства в поля, прикажи висушити всі моря і океани, прикажи розтопити всі льоди і сніги і весь цей простір засіяти пшеницею. Віддавши весь урожай з цих полів, ти розрахуєшся з Сетою.

 

Щоб узнати, чим закінчилася ця історія, нам необхідно вияснити, як же рахували придворні математики , тобто, як обчислюється сума п перших членів геометричної прогресії?

  Отже,

нехай   S_n = b₁+b₁q+b₁q²+b₁q³+…+b₁q^n-2+b₁q^n-1.

 

Помножимо обидві частини цієї нерівності на q:

            S_nq = b₁q+b₁q²+b₁q³+…+b₁q^n-1+b₁qⁿ.

 

Віднімемо почленно від цієї рівності попередню. При цьому їх однакові доданки взаємно знищаться. В результаті маємо:

 

                   S_nq – S_n = b₁qⁿ – b₁,

 

або            S_n(q – 1) = b₁(qⁿ – 1),

 

звідки       S_n = .

 

 

 

Закріплення вивченого матеріалу:

 

 2. Задача «Купівля коня»

Дехто продав коня за 156 рублів, але покупець роздумав купувати і повернув коня продавцю. Тоді продавець запропонував йому інші умови: "Якщо по-твоєму ціна коня висока, то купи тільки цвяхи з його підков, а коня одержиш тоді на додачу безкоштовно. Цвяхів у кожній підкові 6. За перший цвях заплати мені копійки, за другий  копійки, за третій - 1 копійку і т.д."

Покупець, спокушений низькою ціною і бажаючи задарма одержати коня, прийняв умови продавця, розраховуючи за цвяхи заплатити не більше 10 руб. На скільки проторгувався покупець?

Розв’язання.

     :

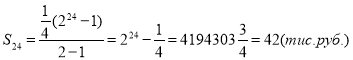
Відповідь: За таких умов можна дати і коня в додачу.

 

 

А тепер повернемося до нашої легенди:

• Назви ж мені це страшне число,- сказав цар.
• Вісімнадцять квінтильйонів чотириста сорок шість квадрильйонів сімсот сорок чотири трильйони сімдесят три більйони сімсот дев’ять мільйонів п’ятсот п’ятдесят одна тисяча шістсот п'ятнадцять, о повелителю!

18446744073709551615.

 

Якщо побудувати зерносховище шириною 10м і висотою 4 м, то його довжина буде на відстань 300 000 000 км, тобто вдвічі більша, ніж від Землі до Сонця!

Домашнє завдання.

 

Підрахувати, скільки зерна мав одержати Сета.

Розв’язати № 287,293(для бажаючих)

 

Додаток А

 

Цікаві факти о прогресії.

 

Всі ми читали задачі та легенди, що приводять до появи великих чисел. Це легенда про нагороду для винахідника шахів, історія про багатого і бідного, який приносив по 10 тисяч рублів, а забирав подвоєну копійку. Але закони прогресії з’являються не лише у вигаданих історіях, а і описують реальні процеси в біології.

Знання теорії великих чисел потрібне не тільки математикам, а й простим людям, щоб не потрапити в ситуації, які можуть вийти з-під вашого контролю.

В Америці спочатку не було горобців. Ця звична для нас пташка була завезена в США з метою знищення шкідливих комах. Горобець, як відомо, у великій кількості поїдає гусінь та інших комах. В Америці не було хижаків, які б знищували цих птахів, і горобець став швидко розмножуватись. Скоро горобців стало так багато, що їм не вистачало шкідників саду. Вони взялися за знищення посівів фермерів. Фермери розпочали війну з горобцями, яка обійшлася дуже дорого. Зараз в США видали закон, який забороняє ввіз будь-яких нових видів тварин.

В Австралії, коли материк був відкритий європейцями, не було кроликів. Кролик був завезений лише в кінці 18 ст. За відсутності хижаків розмноження цих тварин почалось надзвичайно швидко. Вони заполонили всю Австралію, завдаючи величезних збитків сільському господарству, і стали справжнім лихом. Тільки завдяки спеціальним заходам (винайденому спеціально вірусу) вдалося подолати лихо. Приблизно те саме повторилося пізніше з кроликами в Каліфорнії.

Третя повчальна історія відбулася на острові Ямайка. Тут водилися у великій кількості ядовиті змії. Для зменшення їхньої популяції на острів завезли птаха-секретаря. Через деякий час кількість змій різко зменшилась, зате розплодилися пацюки, яких раніше знищували змії. Пацюки приносили таку шкоду плантаціям цукрової тростини, що довелося серйозно задуматися над їх знищенням. Відомо, що ворогом щурів є індійський мангуст. Було вирішено завезти на острів 4 пари і дати їм можливість вільно розмножуватися. Мангусти теж швидко пристосувалися до нової батьківщини і швидко заселили весь острів. Через 10 років  вони знищили пацюків і стали їсти все, що їм траплялося: домашню птицю, кіз, поросят, навіть собак. А з часом мангусти стали загрозою для садів, полів та плантацій. Жителі тоді почали знищувати своїх недавніх союзників, але їм вдалося тільки обмежити шкоду.

Вчені досліджували питання, чому так швидко розходяться чутки та новини як по школі, так і по всьому місту. Інколи не пройде і кілька годин після пригоди, про яку знало всього декілька осіб, а новина облетіла вже все місто, про неї всі знають, всі чули. Це здається магією. Але створивши математичну модель, ми можемо описати це явище за допомогою формул. Візьмемо для прикладу місто, в якому 50000 населення, і уявимо, що о 8 годині ранку трапилася пригода, свідками якої були три особи: чоловік, жінка і дитина. Через 15 хвилин вони прийшли на роботу або до школи і розповіли нехай всього трьом своїм знайомим. На це витратили 15 хвилин. Отже, через півгодини новину вже знають 1+3+3*3=13 чоловік. Кожен із 9 обізнаних поділилися ще з трьома своїми знайомими 13+9*3=40 чоловік. Якщо новина і далі буде поширюватися таким чином, то на 9 годину ранку вже знатимуть: 40+(3*27)=121; Ми вже помітили закономірність обрахунку числа людей, що знають новину:1+3+3*3+3*9+3*81+3*243+…=5000. Тобто, 10 раз із інтервалом 15 хвилин новина передавалася мешканцям міста. Отже, через 150 хвилин всі 50 тисяч будуть знати цю новину.