Тригонометричні формули додавання
урок розробка для викладання на рівні стандарт для учнів філологічного спрямування. Урок містить презентацію. Був проведений у 10 класі Пальчиківського навчально виховного комплексу Полтавського району, Полтавської області. В даній розробці є доведення деяких формул та приклади розвязування задач на застосування тригонометричних формул додавання та наслідків з них
План-конспект уроку
з алгебри в 10 класі
Тема: Тригонометричні формули додавання
Мета:
- вивести формули тригонометричних функцій суми і різниці двох чисел. Формулювати вміння користуватися цими формулами для перетворення тригонометричних виразів;
- виховати культуру спілкування в колективі;
- розвиток логічного мислення, пам’яті, уваги та уяви в учнів;
Учні повинні: уміти застосовувати тригонометричні формули додавання при виконанні тотожних перетворень;
Тип уроку: засвоєння нових знань;
Структура уроку:
І. Організаційний етап. (1 хв.)
ІІ. Оголошення теми, мети і завдань уроку (2 хв.)
ІІІ. Вивчення нового матеріалу (15 хв.)
IV. Закріплення нових знань і умінь учнів (23 хв.)
V. Підсумок уроку (2 хв.)
VI. Домашнє завдання (2 хв.)
Хід уроку
І. Організаційний момент
ІІ. Оголошення теми, мети та завдань уроку
Розповідь вчителя: Сьогодні ми продовжуємо знайомитися з таким серйозним розділом алгебри, як тригонометрія. Як ми вже говорили, що тригонометрія займає значне місце у розвитку таких наук як астрономія, географія, фізика, механіка тощо. На цьому уроці ми з вами спробуємо вивести декілька тригонометричних формул додавання, та спробуємо їх застосовувати для розв’язання тригонометричних виразів.
Але перш ніж переходити до вивчення нової теми давайте пригадаємо формули зведення та їх застосування.
Завдання до класу:
- Спростити вирази:
-
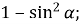
-
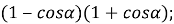
-
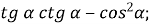
-
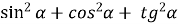 ;
;
-
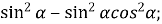
-
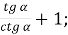
Розв’язання:
-
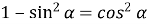 ;
;
-
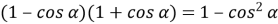 ;
;
-

-
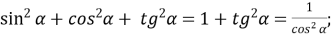
-
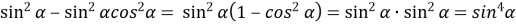 ;
;
-
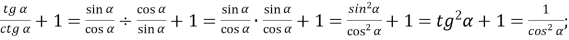
ІІІ. Вивчення нового матеріалу
Розповідь учителя: На попередніх уроках ми виконували тотожні перетворення тригонометричних функцій одного й того самого аргументу, на цьому уроці ми доведемо тригонометричні тотожності додавання для двох різних кутів.
![]()
(показ презентації )
Візьмемо довільну пряму m і точку О на ній. Відкладемо два різні гострі кути ![]()
![]()
![]()
![]()

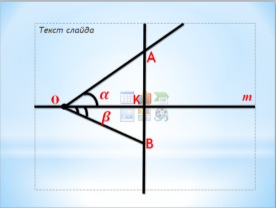
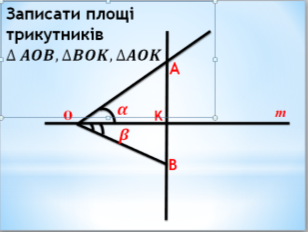
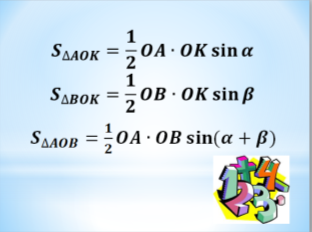




Аналогічно доводитимемо ![]() .
.
Візьмемо довільну пряму m і точку О на ній. Відкладемо два різні гострі кути ![]()
![]()
![]()
![]()
![]()

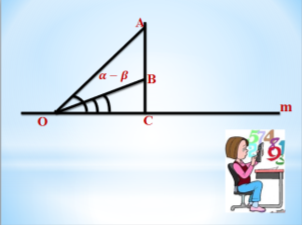
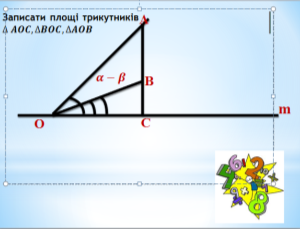






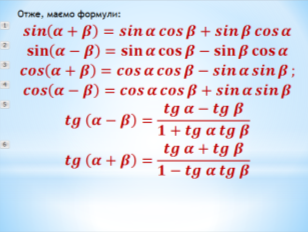
IV. Закріплення нових знань і вмінь учнів
Розв’язування вправ усно.
(Завдання на листочках записано на дошці). Завдання до класу.
- Закінчіть обчислення:
Розв’язання:
- Знайти значення виразу:
Розв’язання:
-
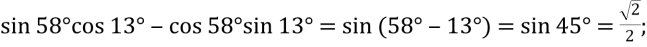
-
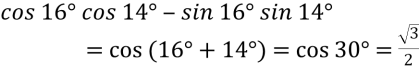 ;
;
-
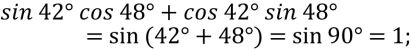
-
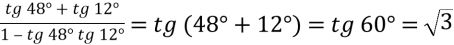 ;
;
-
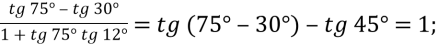
Робота в парах :
№1 обчислити ![]()
№2 обчислити ![]()
Розв’язання:
№1 ![]()
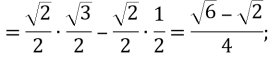
№2 ![]()
Письмові вправи
- Знайдіть значення виразу:
Розв’язання
-

-
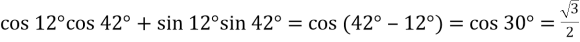
-
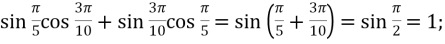
-
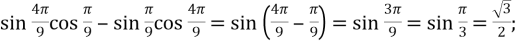
-
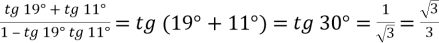 ;
;
-
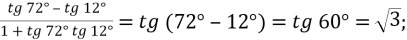
V. Підбиття підсумків уроку
-
Чому дорівнює
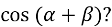
-
Чому дорівнює
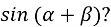
-
Чому дорівнює
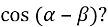
-
Чому дорівнює
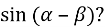
-
Чому дорівнює
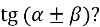
VI. Домашнє завдання
- Спростити вирази:
![]()
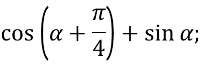
- (Високий рівень)
Довести формули для ![]()


про публікацію авторської розробки
Додати розробку

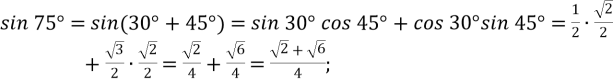
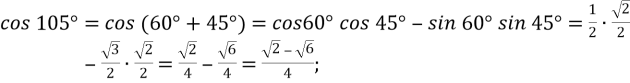
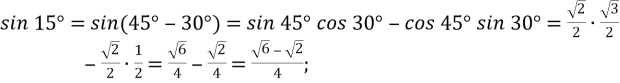

-

Рєзнік Інна Григорівна
09.01.2023 в 16:30
Дякую.
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Опята Людмила Іванівна
18.10.2021 в 21:13
Дякую!!!!
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Дмитренко Людмила Миколаївна
25.01.2021 в 19:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Добридна Світлана Іванівна
31.03.2020 в 13:27
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Катрін Альона Анатоліївна
25.11.2018 в 22:31
Дякую за розробку уроку!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука