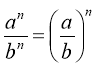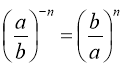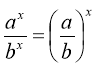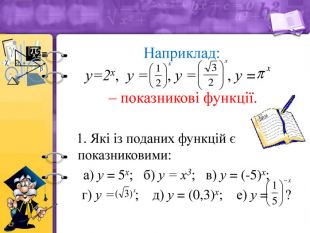Заняття на тему: "Показникова функція, її властивості та графік"
Під час проведення заняття використано різноманітні форми роботи з групою: фронтальна бесіда, самостійна робота, тренувальні вправи, випереджувальні завдання, самостійна робота, ілюстрації, елементи ігрових технологій
- функція.docx docx
- функція.pptx pptx
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
МОГИЛІВ – ПОДІЛЬСЬКИЙ ТЕХНОЛОГО – ЕКОНОМІЧНИЙ КОЛЕДЖ
ВІННИЦЬКОГО НАЦІОНАЛЬНОГО АГРАРНОГО УНІВЕРСИТЕТУ

Заняття – лекція на тему:
"Показникова функція, її властивості та графік"
методична розробка відкритого заняття
з дисципліни «Математика»
Методична мета заняття: реалізація інформаційно – комунікативних технологій, творчої складової в процесі формування вмінь та навичок студентів, застосування активних форм і методів виховання особистості компетентного спеціаліста.
Узагальнення – це, мабуть, найлегший найочевидніший шлях розширення
математичних знань.
В.Сойер
Тема заняття: Показникова функція, її властивості та графік.
Вид заняття: інтерактивна лекція.
Мета заняття:
Навчальна: розглянути фізичні моделі, пов‘язані з процесами органічної зміни
величин, що дозволяють дати означення показникової функції,
перелічити її властивості та побудувати її графік
Розвиваюча: розвивати продуктивне мислення студентів
Виховна: виховувати толерантність, вміння співпрацювати, культуру
математичних записів, інтерес до вивчення математики.
Предметні компетенції заняття: навчальна, соціально – трудова, стимулювально – мотиваційна.
Функції:
Теоретична: поняття показникової функції , властивості, графік .
Практична: будувати графіки показникової функції.
МПЗ: Забезпечуючі: Математика «Степінь з довільним показником та
його властивості», «Графіки функцій та їх властивості»
Забезпечувані: Фізика «Фізика атомного ядра»,
Біологія «Молекулярні основи біології»
Мікробіологія «Розмноження бактерій».
Забезпечення заняття:
1. Література: М.І. Шкіль. Алгебра і початки аналізу. 10 клас
О.М. Роганін. Плани – конспекти уроків.
Т.Г.Роєва. Алгебра в таблицях.
- Наочні посібники: презентація “Показникова функція, її властивості і графік“,
- Роздатковий матеріал: опорний конспект. «Показникова функція».
- Технічні засоби навчання. Мультимедійний проектор.
Хід заняття
- Організаційна частина заняття
(Метод: психолого – педагогічної підтримки роботи студентів на занятті, рефлексія)2 хв.
Мета етапу: створення сприятливого психологічного клімату на занятті.
Викладач. Шановні студенти сьогодні на занятті ми працюватимемо разом, я розраховую на вашу підтримку та допомогу. Кожному з вас я хочу побажати, щоб на цьому занятті ви були:
„У"- усміхненими
„С"- спокійними
„П"- прогресивними
„І"- ініціативними
„X"- хоробрими
Іншими словами, я бажаю вам УСПІХУ!
І не тільки на заняттях математики, бо якщо звернутись до слів філософа Е.Ільєнков. то можна зазначити: Досягнення успішного результату під час розв'язування задач - зовсім не привілей математики. Усе людське життя - це не що інше, як постійне бажання досягти успіху у вирішенні нових питань та проблем.
Підніміть руку, хто бажає досягти успіху? Я теж бажаю досягти успіху.
ІI. Підготовка студентів до заняття.
Мета етапу: організувати цілеспрямовану діяльність студентів:
- розвинути внутрішню мотивацію студентів до теми, що вивчається;
- навчити студентів прогнозувати очікувані результати заняття;
- відтворити необхідні знання та вміння для досягнення результатів заняття.
2.1 Повідомлення теми, мети та плану заняття.
(Метод: інструктування).
Тема заняття: Показникова функція, її графік та властивості.
Викладач. Підготуємо наші зошити до роботи. Пам'ятайте, що під час роботи з діловою документацією до успіху веде старанне, охайне, уважне ставлення до цієї справи.
Для досягнення успіху нам потрібно сформулювати мету. Сформулюйте і ви нашу мету користуючись словами «знати» та «вміти».
Очікувана відповідь:
Мета заняття: знати показникову функцію, розпізнавати графік показникової
функції, властивості показникової функції;
вміти: будувати графіки і на них ілюструвати властивості
функції, застосовувати показникові функції до опису
найпростіших реальних процесів.
План заняття:
1. Означення показникової функції.
2. Побудова графіка показникової функції.
3. Властивості показникової функції.
2.2 Мотивація навчальної діяльності студентів
( методи – проблемно - пошуковий, реалізація МПЗ)
Викладач. Ми з'ясували, чого хочемо досягти, але на цьому етапі не менше важливим є питання, нащо нам це потрібно, навіщо вивчається ця тема?
1. В природі і техніці часто зустрічаються процеси, які мають спільну назву процесів органічної зміни величин. Ця назва пов‘язана із тим, що такі процеси часто зустрічаються в біології. Значна властивість цих процесів полягає в тому, що за однакові проміжки часу значення величини змінюється в одному і тому ж самому відношенні.
Ці процесів математично виражаються за допомогою показникової функції:
- задача про радіоактивний розпад;
- задача про зміну атмосферного тиску;
- задача про розмноження бактерій;
- задача про вакуумування;
- задача про приріст деревини.
Проблема.
Наведемо приклади, в яких величини змінюються по вказаному вище закону.
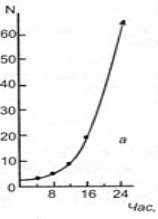 Приклад 1. Ще в XVII ст. було встановлено, що чисельність популяцій зростає за законом геометричної прогресії, а вже в кінці XVIII ст. Томас Мальтус (1766-1834) висунув свою відому теорію про зростання народонаселення в геометричній прогресії. Ця закономірність зростання виражається кривою, зображеною на рис. Сучасною математичною мовою ця крива відображає експоненційний ріст чисельності організмів і описується рівнянням:
Приклад 1. Ще в XVII ст. було встановлено, що чисельність популяцій зростає за законом геометричної прогресії, а вже в кінці XVIII ст. Томас Мальтус (1766-1834) висунув свою відому теорію про зростання народонаселення в геометричній прогресії. Ця закономірність зростання виражається кривою, зображеною на рис. Сучасною математичною мовою ця крива відображає експоненційний ріст чисельності організмів і описується рівнянням:
Nt = N0er,
де: Nt - чисельність популяції в момент часу t;
N0 - чисельність популяції в початковий момент часу t0; е - основа натурального логарифма (+2,7182); r - показник, що характеризує темп розмноження особин в даній популяції. Якщо колонія бактерій має достатній простір і достатню кількість поживних речовин, то її маса за рівні проміжки часу збільшується в одному і тому ж відношенні. В таких випадках говорять про процеси органічного росту.
Приклад 2. Радіоакти́вність(радіоактивний розпад) (від лат. radio — «випромінюю» radius — «промінь» і activus — «дієвий») — явище мимовільного перетворення нестійкого ізотопа хімічного елементу в інший ізотоп (зазвичай іншого елемента) шляхом випромінювання гамма-квантів, елементарних частинок або ядерних фрагментів.
При радіоактивному розпаді маса речовини змінюється по наступному закону: за рівні проміжки часу вона змінюється в одному і тому ж відношенні. Такі процеси називають процесами органічного спадання.
Взагалі, частка частинок, що залишаються залежить від часу t таким чином:
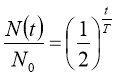
Величини періодів напіврозпаду для різних ізотопів різні; для одних ізотопів, що швидко розпадаються, період напіврозпаду може бути рівним мільйонним часткам секунди, а для інших ізотопів, таких як 238U або 232Th, він дорівнює 4,5 млрд років та 14 млрд років відповідно.
У всіх розібраних прикладах значення виразу а t при всіх значеннях t додатнє. При а>1 значення а t збільшується (як у випадку розмноження бактерій), а при 0< а<1 значення а t зменшується з ростом t (як у випадку радіоактивного розпаду). Отже, для описання таких процесів, як радіоактивний розпад або розмноження бактерій, потрібна функція ах, де а>0.
Отже ми розуміємо актуальність того над чим працюємо для виконання різних завдань, підсумкового оцінювання, домашніх завдань, для продовження навчання та вивчення інших наук.
2.3 Актуалізація опорних знань та вмінь студентів
( методи – метод „ Мікрофон ", пояснювально – ілюстративний;
форма роботи - презентація, діалог)
1. Пригадати властивості степеня з довільним показником:
6.
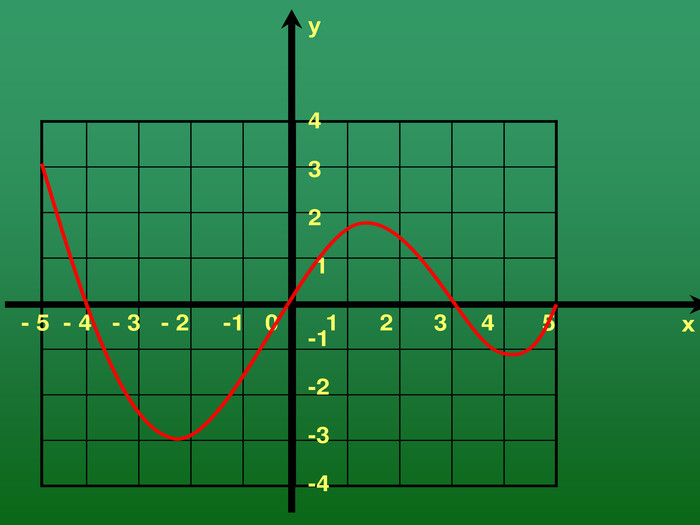
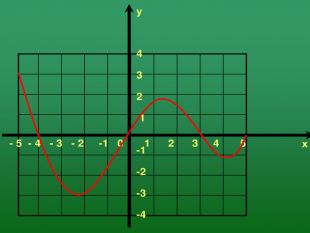
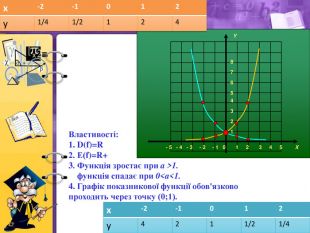
2. Записати властивості функції по її графіку.
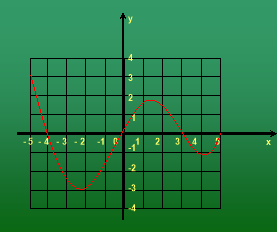
Очікувана відповідь:
D (f) = R
E (f): ( -3; +∞)
Функція ні парна, ні непарна.
Функція зростає при х![]() ( -2,2; 1,2)U( 4,1; +∞)
( -2,2; 1,2)U( 4,1; +∞)
Функція спадає при х![]() ( -∞; -2,2)U( 1,2; 4,1)
( -∞; -2,2)U( 1,2; 4,1)
IІІ. Вивчення нового матеріалу
( метод – інформаційно - комунікативний).
1. Означення показникової функції.
Показниковою функцією називається функція виду у=ах, де а>0 і а![]() 1.
1.
Наприклад: у=2х, у=![]() х, у=
х, у=![]() х, у=
х, у=![]() х – показникові функції.
х – показникові функції.
ІV. Закріплення вивченого матеріалу
( метод – навчальний тренажер)
1. Які із поданих функцій є показниковими:
а) у = 5х; б) у = х3; в) у = (-5)х; г) у = (![]() )х; д) у = (0,3)х; е) у =
)х; д) у = (0,3)х; е) у = ![]() ?
?
2. Побудова графіка показникової функції.
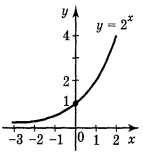 2.1. Функція виду у = 2х.
2.1. Функція виду у = 2х.
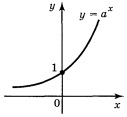
Графіком показникової функції є крива, яка називається експонентою.
1. Нехай з початку спостережень маса колонії бактерій дорівнювала 1 г, причому за кожну наступну годину вона зростала в 2 рази. Побудуємо графік зміни маси m в залежності від часу х.
Залежність між масою і часом виражається формулою m=2х. Для побудови графіка обчислимо масу колонії через 1, 2, 3, години до початку і після початку спостереження.
Дані обчислювання занесемо в таблицю, вважаючи, що час до початку спостереження був відємним.
Складемо таблицю значень функції:
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у= 2х |
|
|
1 |
2 |
4 |
Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Одержимо графік функції у = 2х
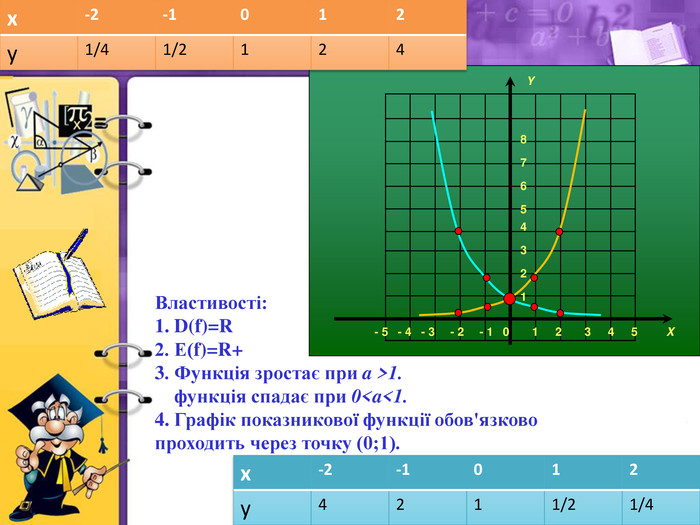
Показникова функція у = 2х має властивості:
1. Область визначення — множина всіх дійсних чисел. D(ax)=R
2. Область значень — множина всіх додатних чисел. Е(ax)=(0;+![]() )
)
3. Функція у = 2х — зростаюча на множині всіх дійсних чисел.
4. Графік функції перетинає вісь у в точці(0; 1).
На цьому графіку наочно видно уже відомі властивості цієї функції: із зростанням х значення функції зростають, при чому при достатньо великих значеннях х значення 2х стають як завгодно великими (наприклад, 210=1024, 220=1048576 і т.д.).
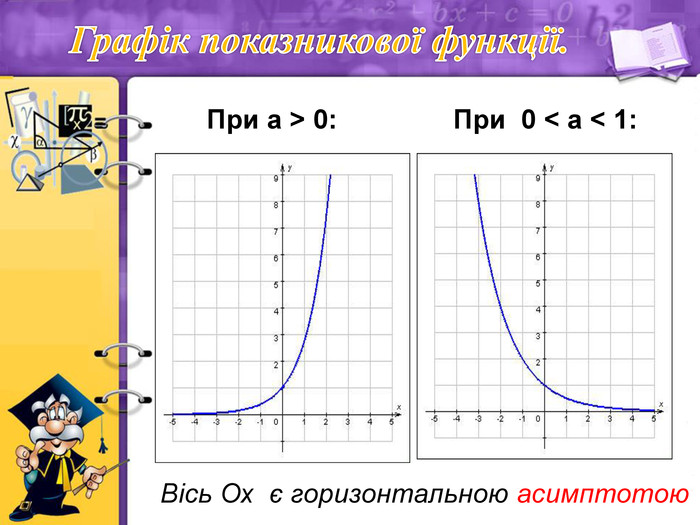
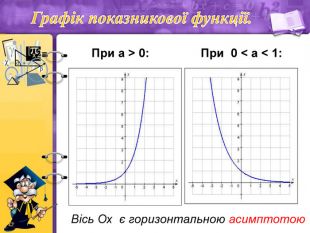
Схожі на вигляд графіки функцій ах при будь-якій основі а, більшій за 1.
2.2. Функція виду у = ![]() .
.
2) Маса радіоактивної речовини змінюється по закону m=m0(![]() )t. Побудуємо графік зміни маси радіоактивної речовини в часі, вважаючи, що початкова маса m0=1 г.
)t. Побудуємо графік зміни маси радіоактивної речовини в часі, вважаючи, що початкова маса m0=1 г.
Для цього використаємо рівність ![]() . Ця рівність показує, що таблицю значень функції
. Ця рівність показує, що таблицю значень функції ![]() одержуємо із таблиці значень функції 2х зміною знаків у першому рядку
одержуємо із таблиці значень функції 2х зміною знаків у першому рядку
 Побудуємо графік функції у =
Побудуємо графік функції у = ![]() , для цього складемо таблицю значень функції:
, для цього складемо таблицю значень функції:
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у = |
4 |
2 |
1 |
|
|
Побудуємо на координатній площині точки з таблиці і з'єднаємо ці точки плавною лінією. Одержимо графік функції у = ![]() .
.
Показникова функція у = ![]() має властивості:
має властивості:
1. Область визначення — множина всіх дійсних чисел. D(ax)=R
2. Область значень — множина всіх додатних чисел. Е(ax)=(0;+![]() )
)
3. Функція у = ![]() — спадна на множині всіх дійсних чисел.
— спадна на множині всіх дійсних чисел.
4. Графік функції перетинає вісь у в точці (0; 1).
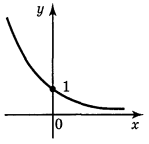
По рис. бачимо, що всі значення ![]() також додатні, але ці значення зменшуються при збільшенні х.
також додатні, але ці значення зменшуються при збільшенні х.
Схожий вигляд мають графіки показникової функції ах при 0< а<1.
Вісь Ох є горизонтальною асимптотою.
ІV. Закріплення вивченого матеріалу
( методи – тренувальні вправи).
2. Які з наведених показникових функцій є зростаючими, а які — спадними:
 а) y = πx ; б) y = (0,5)x; в) у =
а) y = πx ; б) y = (0,5)x; в) у = ![]() ; г) y = 2-x.
; г) y = 2-x.
Відповідь: а) зростаюча; б) спадна; в) зростаюча; г) спадна.
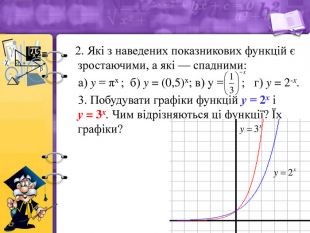
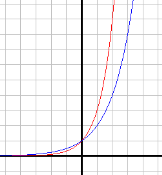
3. Побудуємо графіки функцій у = 2х і у = 3х. Чим відрізняються ці функції? Їхні графіки?
Відповідь: ці функції мають одинакові властивості, функція у = 3х зростає більш швидше (графік цієї функції піднімається вгору більш круто).
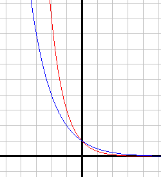
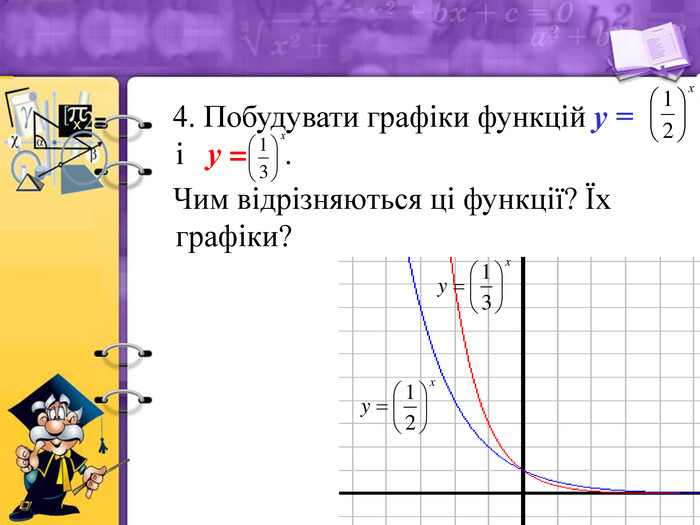
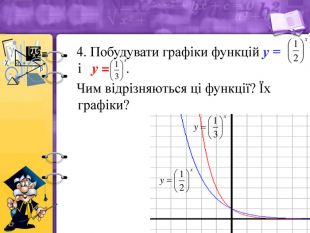
4. Чим відрізняються властивості і графіки функцій у =![]() і у=
і у= ![]() ?
?
Відповідь: вони мають однакові властивості, функція у = ![]() спадає більш швидше.
спадає більш швидше.
3. Властивості показникової функції.
1) Область визначення: х![]() R. D(ax)=R
R. D(ax)=R
2) Область значень: у>0 Е(ax)=(0;+![]() )
)
3) Функція ні парна, ні непарна
4) Вірні рівності а1= а і а0=1.
5) Якщо а>0, то функція ах зростає на всій області визначення;
якщо 0< а<1, то вона спадає на всій області визначення.
6) Найбільшого і найменшого значень функція не має.
7) Для будь-яких дійсних значень m і n (а>0; b>0) виконуються рівності:

ІV. Закріплення вивченого матеріалу
( методи – закріплення і корекції знань, умінь, навичок).
5. Порівняйте значення виразів:
а) ![]() і
і ![]() ; б) 2-3 і 2-4; в) 0,30,7 і 1
; б) 2-3 і 2-4; в) 0,30,7 і 1
Відповідь: а) ![]() <
< ![]() ; б) 2-3 > 2-4; в) 0,30,7 < 1 .
; б) 2-3 > 2-4; в) 0,30,7 < 1 .
6. Порівняйте х і у, якщо відомо, що вірна нерівність:
а) 0,02х < 0,02y; б) πx > πy.
Відповідь: а) х > у; б) x < у.
7. Обчислити: а) 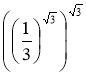 ; б)
; б) ![]()
V. Узагальнення ти систематизація знань,умінь та навичок студентів
(методи – складання та аналіз узагальнюючої таблиці, сканворд)
|
Показникова функція у = ах, а > 0, а ≠ 1
|
|
|
а > 1 |
0 < а < 1 |
|
1. D(y) = R
2. Е(у) = (0; + 3. Зростає
x1 > x2 4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у < 1 6. Якщо х > 0, то у > 1
|
1. D(y) = R
2. E(y) = (0; + 3. Спадає
x1 > x2 4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у > 1 6. Якщо х > 0, то у < 1
|
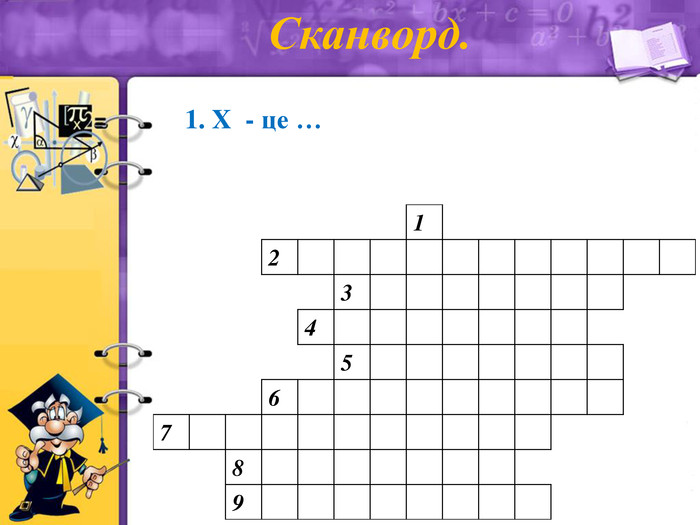
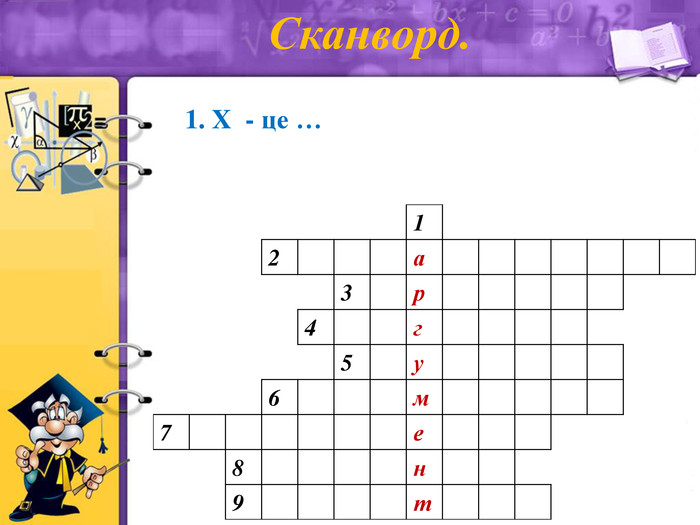
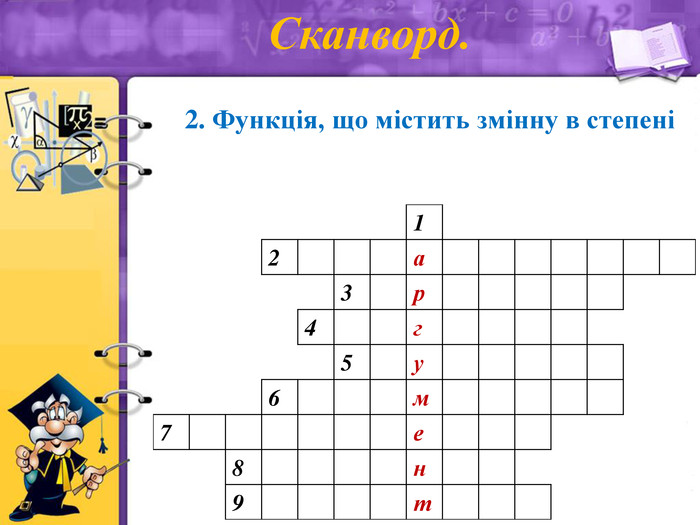
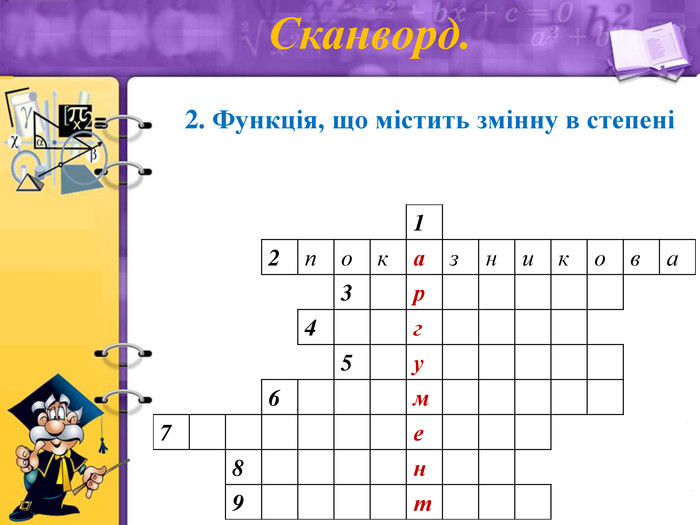
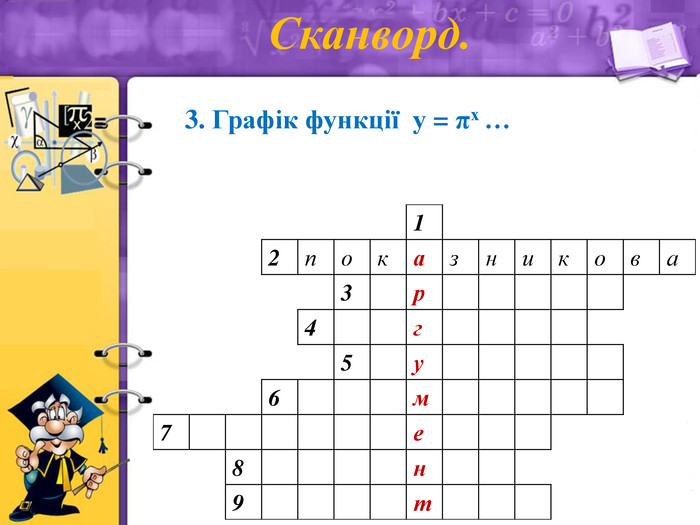
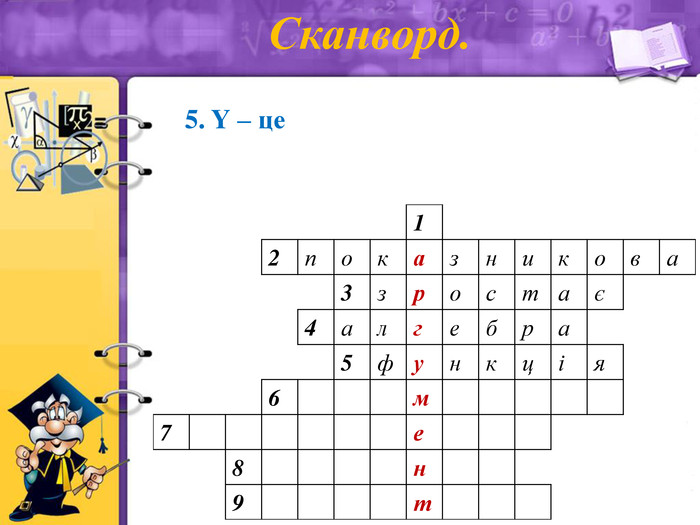
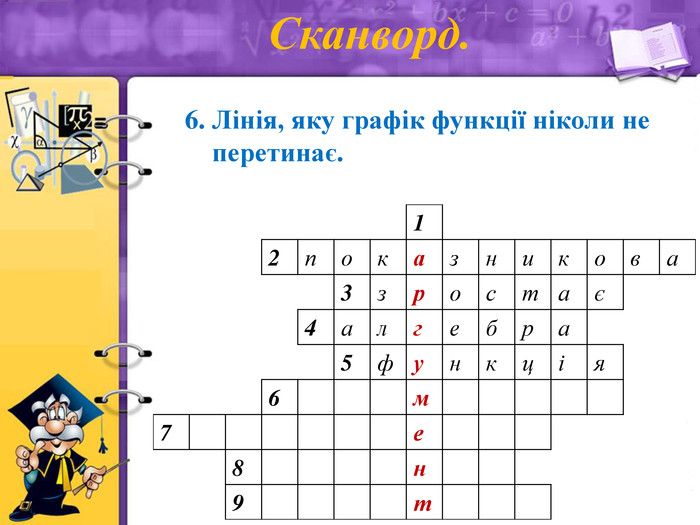
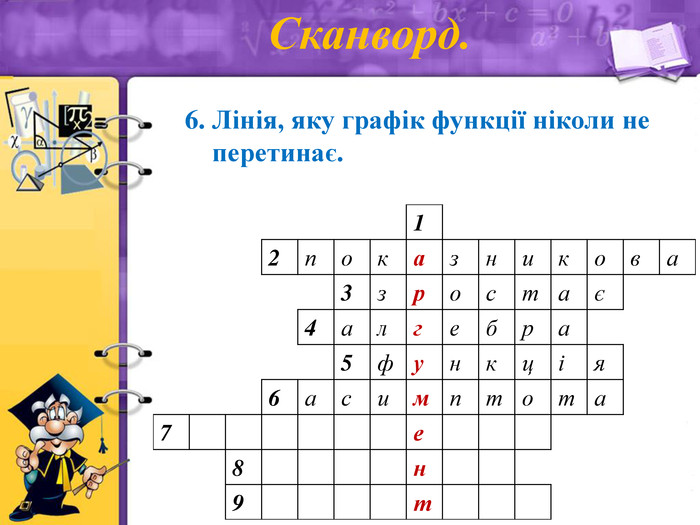
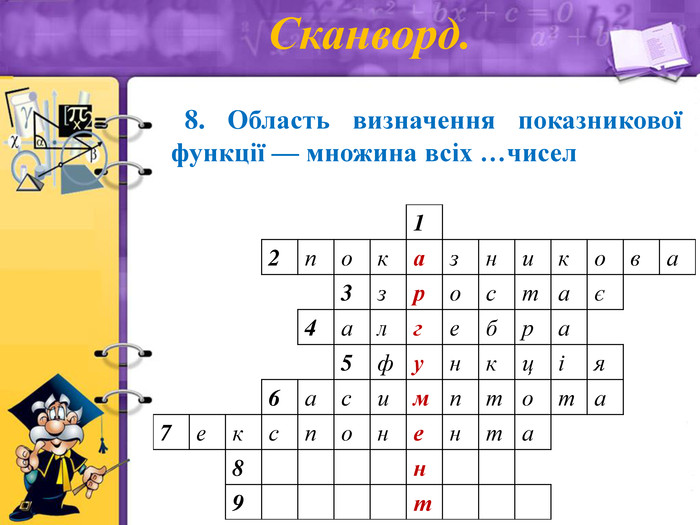
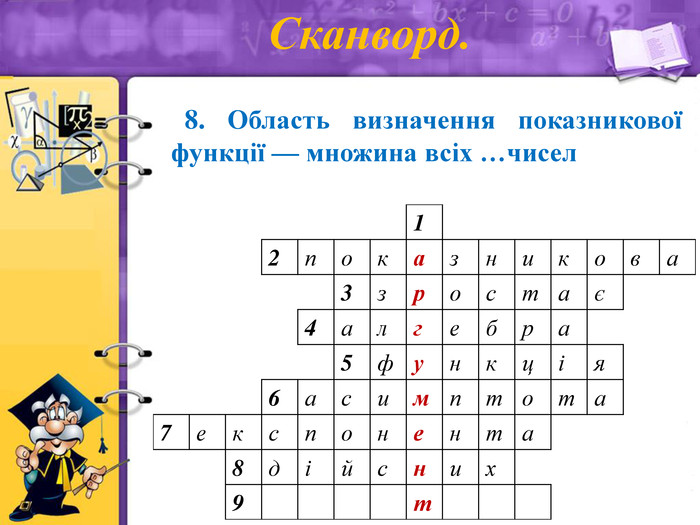
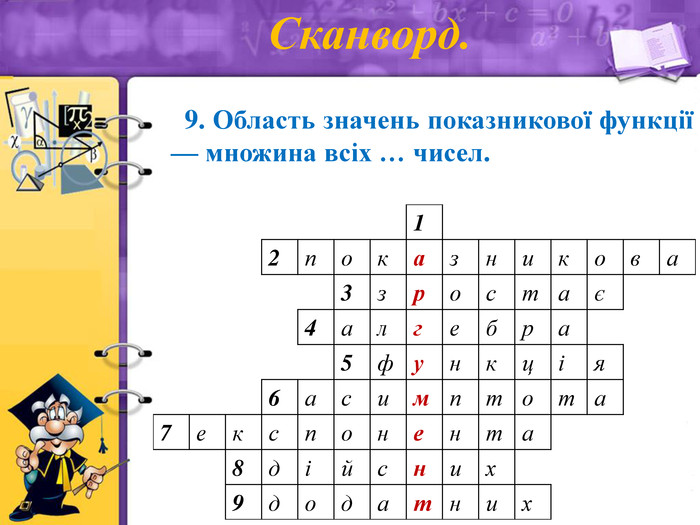
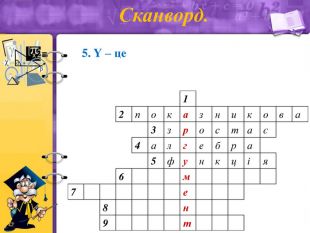
Сканворд.
1. X - це (аргумент)
2. Функція, що містить змінну в степені (показникова)
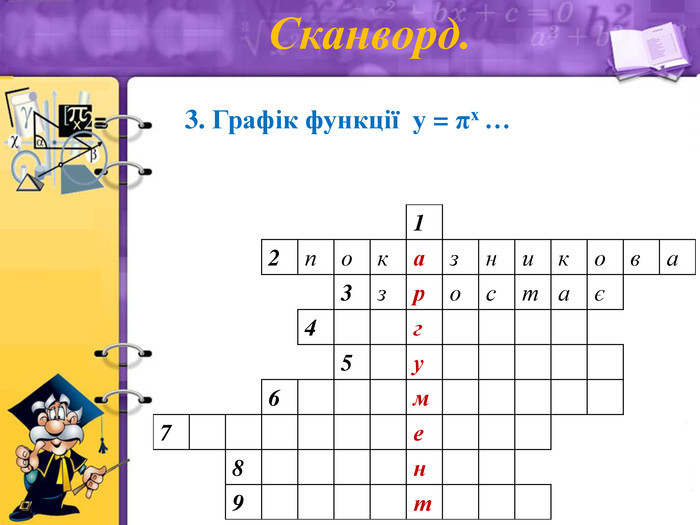
3. Графік функції у = πх … (зростає)
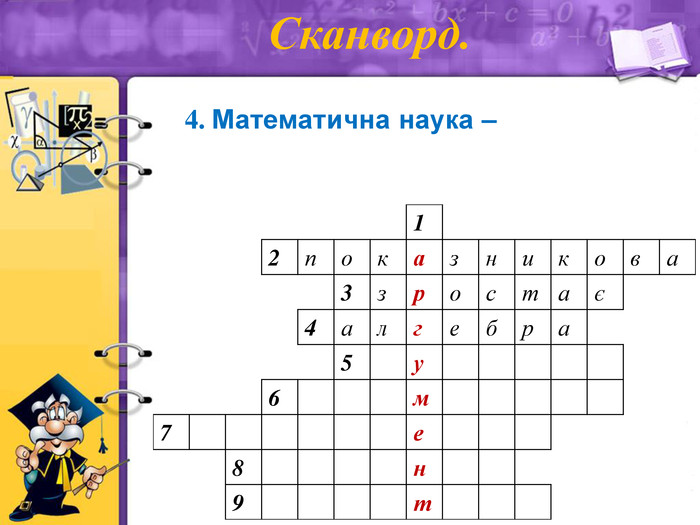
4. Математична наука – (алгебра)
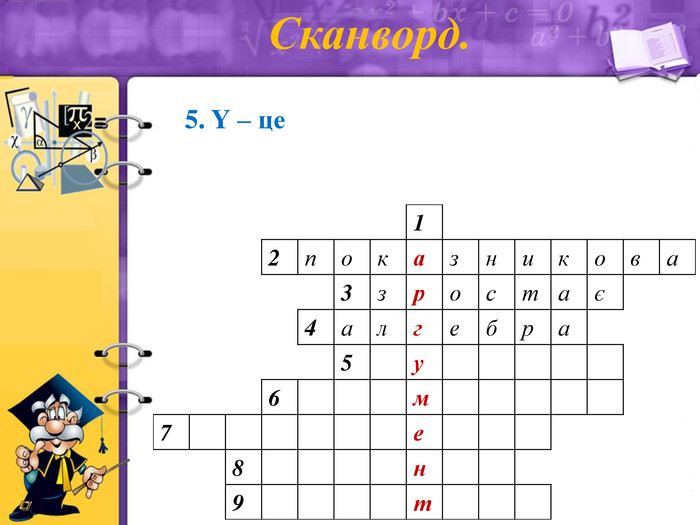
5. Y – це (функція)
6. Лінія, яку графік функції ніколи не перетинає (асимптота)
7. Графіком показникової функції є крива, яка називається (експонента).
8. Область визначення показникової функції — множина всіх (дійсних) чисел.
9. Область значень показникової функції — множина всіх (додатних) чисел.
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
п |
о |
к |
а |
з |
н |
и |
к |
о |
в |
а |
|
|
|
|
|
|
3 |
з |
р |
о |
с |
т |
а |
є |
|
|
|
|
|
|
|
4 |
а |
л |
г |
е |
б |
р |
а |
|
|
|
|
|
|
|
|
|
5 |
ф |
у |
н |
к |
ц |
і |
я |
|
|
|
|
|
|
6 |
а |
с |
и |
м |
п |
т |
о |
т |
а |
|
|
|
7 |
е |
к |
с |
п |
о |
н |
е |
н |
т |
а |
|
|
|
|
|
|
|
8 |
д |
і |
й |
с |
н |
и |
х |
|
|
|
|
|
|
|
|
9 |
д |
о |
д |
а |
т |
н |
и |
х |
|
|
|
|
VІ. Підведення підсумків заняття.( рефлексія)
Мета етапу: Визначити чи досягнуті, мета, очікувані результати заняття
провести рефлексію.
Студентам пропонується закінчити речення
1. Було цікаво…
2. Було важко…
3. Я навчилась…
4. У мене вийшло…
Таким чином, для успіху потрібно: «самоконтроль», «співпраця», «досконала
підготовка». Але протягом уроку ми весь час працювали з партнерами, могли
отримати допомогу, а в житті дуже часто випадає розраховувати на свої сили. І
цього теж потрібно вчитись. Це одна з причин виконання домашніх завдань.
VІІ. Домашнє завдання.
Конспект, М. І. Шкіль Алгебра 10 клас. § 19 с. 189-202
1. Порівняйте значення виразів:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]()
2. Побудувати графіки функцій та записати властивості:
а) у = 3х-2; б) ![]()
3. Обчислити: а) 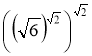 ; б)
; б) ![]() .
.
Викладач
Висновок:
Чи існує універсальна форма успіху, чи одержали ми її сьогодні на занятті? Це питання належить до розряду проблем, пошуку філософського каменя, створення вічного двигуна, побудови машини часу. Але без віри людини у можливість у їх створення, не було б кроку вперед, не було б прогресу.
Хочу подякувати вам за заняття, ще раз побажати успіху і сказати, що я вірю у ваш успіх. На згадку про наше заняття запам’ятайте ще один рецепт успіху: „Успіх - це тільки 10% таланту і 90% щоденної наполегливої праці."
Притча:
Ішов Мудрець, а назустріч йому три чоловіки, які везли під гарячим сонцем візки з камінням для будівництва. Мудрець зупинився і задав кожному запитання. У першого запитав «Що ти робив цілий день?». І той відповів, що цілий день возив це важке каміння. У другого запитав мудрець «А що ти робив цілий день?», і той відповів: «А я добросовісно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: « А я приймав участь у будівництві храму!»
І ми сьогодні на занятті приймали участь у будівництві храму – храму науки.
Бажаю всім ще кращих результатів. Дякую за роботу!
1


про публікацію авторської розробки
Додати розробку