Тригонометричні тотожності. Синус, косинус, тангенс кутів від 0° до 180°

Конспект уроку геометрії  9 клас

Тема уроку.  Тригонометричні тотожності. Синус, косинус, тангенс кутів від 0° до 180°

Мета: активізувати знання учнів про залежності між сторонами і кутами прямокутного трикутника; формування понять синуса, косинуса, тангенса кутів від 0° до 180°; формування вмінь визначати тригоно­метричні функції довільних кутів.

Формування предметних компетентностей:

ознайомити учнів зі знаходження значень синуса, косинуса і тангенса тупих кутів, повторити тригонометричні формули, розв’язання практичних завдань,; удосконалювати вміння учнів працювати з QR-кодом, диференційованими завданнями; розвивати аналітичне мислення, техніку швидких обчислень, пам’ять, увагу; виховувати допитливість.

Формування ключових компетентностей:

спілкування державною мовою (уміння усно і письмово висловлювати власну думку, тлумачити поняття та ін.);

уміння навчатися впродовж життя (уміння сприймати й аналізувати інформацію, визначати головне, формулювати, складати алгоритм навчальної діяльності та дотримуватися його, організовувати робоче місце, оцінювати результати роботи – своєї та однокласників);

соціальні та громадянські (здатність працювати в групі (команді) на результат, досягати компромісів, виховувати почуття відповідальності за успіх команди);

загальнокультурну грамотність (бережливе ставлення до шкільного майна і оханість при письмі);

математична компетентність (вміння знаходити тригоно­метричні функції тупих кутів, застосовувати вивчені означення і властивості).

Обладнання: лист оцінювання знань, картки із завданнями, підручники, LEGO, QR-коди.

Очікуваний результат:

• учні можуть наводити приклади співвідношень, указаних у змісті;
• пояснювати: що таке синус, косинус, тангенс кутів від 0° до 180°,
• застосовувати вивчені формули та означення
• працювати в парі;
• працювати в групі;

Хід уроку

І. Мотивація навчально-пізнавальної діяльності учнів

Перевірка готовності класу до уроку. Учні об'єднані у 4 групи. Кожна група має консультанта, який отримає лист оцінювання знань.

ІІ. Актуалізація опорних знань і способів дій

Перевірка домашнього завдання

1. Консультанти груп перевіряють наявність домашнього завдання та готують питання, якщо не зрозуміло.
2. Учитель слухає доповіді та пропонує скласти план обговорення теоретичних аспектів попереднього уроку. А саме:

 1) Кут, як геометрична фігура. Міри кутів і дуг.

 2) Прямокутна система координат.

 3) Визначення тригонометричних функцій довільного кута.

 4) Знаки тригонометричних функцій за кутами.

3. Далі кожна команда отримує картку із завданнями подібними до домашнього та спілкуючись та допомагаючи один одному, розв’язує їх.
4.  Обговорюємо та перевіряємо виконання, звертаємо увагу на поширені помилки. Далі повторюємо ще раз теоретичні аспекти за планом.

ІІІ. Формування нових знань і способів дій

 Означення синуса, косинуса і тангенса кутів від 0° до 180°

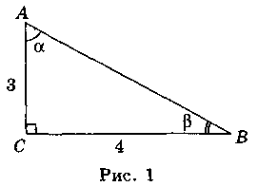
Побудує­мо коло з центром у початку координат і радіусом 1 (рис. 2). Таке коло називається одиничним. Побудуємо гострий кут а, який утворює радіус ОА цього кола з додатним напрямом осі Ох. Нехай точка А має координати (х; у). Тоді для прямокутного трикутника АОВ маємо:

sinα = = = у;  cosα = = = x;  tgα = = .

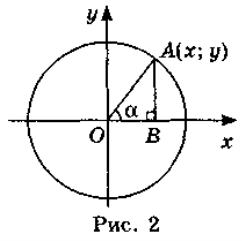
Таким чином: синусом кута α є ордината точки А одиничного кола, причому радіус ОА утворює з додатним напрямом осі Ох кут α. Косинусом кута α є абсциса точки А одиничного кола, при­чому радіус ОА утворює з додатним напрямом осі Ох кут α. Тан­генсом кута α є відношення ординати точки А до абсциси цієї точ­ки, причому радіус ОА утворює з додатним напрямом осі Ох кут α.

Знаходження значень синуса, косинуса і тангенса тупих кутів

Користуючись наданими означеннями, дамо означення для будь-якого кута α, 0° < α < 180°.

Тоді sin 0° = 0, cos 0° = 1, tg 0° = 0; sin 180° = 0, cos 180° = -l,   tg 180° = 0.

Якщо кут α — тупий (0° < α < 90°), то ордината точки А (рис. 3) додатна (тобто sin α > 0), абсциса — від'ємна (тобто cosα < 0), і відношення ординати до абсциси — від'ємне (тобто tgα < 0).

Отже, косинус, тангенс тупого кута від'ємні.

Якщо α – тупий кут (рис. 4), то cos α = ОС = - OD = -cos (180°- α),

sinα = AC = AD = sin (180° - α), тоді tg α = = - = -tg(180° - α).

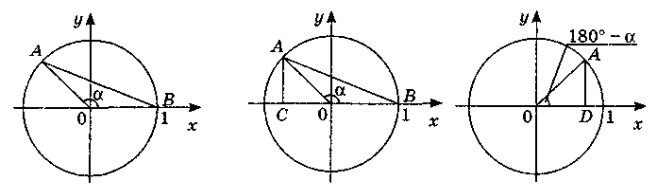
Отже, щоб знайти синус тупого кута, досить знайти си­нус суміжного кута; щоб знайти косинус, тангенс тупого кута, треба знайти число, протилежне косинусу, тангенсу суміж­ного кута.

Наприклад, sin 120° = sin (180° - 120°) = sin 60° = ,

cos 150^o = - cos (180° - 150°) = - cos 30° = - ,

tg 135° = -tg (180° - 135°) = - tg 45° = - 1.

Якщо учні класу мають недостатню математичну підготовку, то можна спростити пояснення. Досить сказати, що синус тупого кута дорівнює синусу суміжного кута, а косинус і тангенс тупого кута до­рівнюють числу, протилежному косинусу і тангенсу суміжного кута.

IV. Закріплення вивченого матеріалу.

Формування вмінь і навичок

1. Робота з підручником, розв’язування завдань і вправ
2. Групова робота. Робота з QR-кодом. Диференційовані завдання

1. Сформулюйте означення: sin, cos, tg гострого кута прямокутного трикутника.
2. Чому дорівнюють значення  sinα, cosα, tgα для кута 0°, 90°, 180°?
3. Як змінюється sinα і cosα, якщо кут α зростає: а) від 0°до 90°; б) від 90°до 180°?
4. Спростіть вираз:

а) 1 + sin²α + cos²α; б) 2cos²α + sin²α – 1.

 V. Рефлексія навчально-пізнавальної діяльності

Робота з LEGO. кожна пара має на парті два кубики lego, учні самостійно встановлюють колір для правильної відповіді та для невірної. Вони працюють над завданням 2 хвилини. Консультанти разом з учителем оцінюють роботу всіх учасників.

Робота в парі

1. Обчисліть синус, косинус і тангенс кута:

а) 120°; б) 135°; в) 150°.

2. Користуючись калькулятором (таблицями), знайдіть:

a) sin 100°, sin 132°, sin 175°;  б) cos 95°, cos 127°, cos l70°;

в) tg 93°, tg 129°, tg 172°.

Що нового ви дізналися на уроці?

Яких значень(додатних чи від’ємних) набуває синус, косинус, тангенс кутів від 0° до 180°. На що слід орієнтуватися?

Що ви повторили? Що закріпили? Які вміння вдосконалили?

Домашнє завдання:  Розробити проект.