Матеріал для факультативу: "Цікаві теореми планіметрії"
Тереми Чеви, Менелая та інші теореми, розглянуті в роботі , дають можливість знаходити відношення відрізків, доводити належність трьох точок одній прямій, розв'язувати задачі про трійки прямих, що проходять через одну точку більш раціональним способом, ніж традиційний, розв'язувати нестандартні задачі підвищеної складності.
Цікаві теореми планіметрії
ЗМІСТ
1.1. Теорема Піфагора і обернена до неї 4
1.2. Різні доведення теореми Піфагора 7
1.3. Узагальнення теореми Піфагора 8
РОЗДІЛ 2. ТЕОРЕМИ ЧЕВИ І МЕНЕЛАЯ 10
2.2. Теорема Менелая і обернена до неї 13
РОЗДІЛ 3. ТЕОРЕМИ КАРНО І ДЕЗАРГА 15
РОЗДІЛ 4. ТЕОРЕМИ ПАСКАЛЯ 1 ПАППА 19
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ 23
ВСТУП
В елементарній геометрії значний інтерес викликають визначні точки та лінії трикутника. Дослідження у цьому напрямі проводились багатьма видатними вченими, починаючи з Архімеда , весь час перебували у полі зору математиків і продовжуються в наш час. Трикутник – одна з найпростіших геометричних фігур , а геометрія трикутника –найцікавіший розділ планіметрії. Над її проблемами працювали найвідоміші вчені всіх часів: Піфагор, Евклід, Архімед, Менелай,
![]() Чева, Дезарг, Торрічеллі, Паскаль,
Лейбніц, Ньютон, Ейлер, Лагранж, Жергон, Понселе та багато інших. Виявлені й
доведені ними теореми про властивосі трикутників справжні перлини математики і
людського мислення взагалі.
Чева, Дезарг, Торрічеллі, Паскаль,
Лейбніц, Ньютон, Ейлер, Лагранж, Жергон, Понселе та багато інших. Виявлені й
доведені ними теореми про властивосі трикутників справжні перлини математики і
людського мислення взагалі.
Трикутники вивчають і використовують майже в кожному класі загальноосвітньої школи , тільки - в мінімальному обсязі. А відомості з геометрії трикутника дають добрий матеріал для досліджень математикам _ початківцям . Багато з них доступні навіть нам – учням основної школи , тому їх можна використовувати і в навчанні геометрії .
" Геометрія трикутника перетворилась у струнку й офіційно визнану наукову дисципліну. Тісні взаємини цієї дисципліни зі шкільною математикою , з одного боку, і з широким полем вищої геометрії - з другого , роблять її природним містком між першою і другою…" так писав харьківський методист Ю. М. Гайдук майже півстоліття тому, але й тепер інтерес до геометрії трикутника не слабне.
У своїй роботі я розглянула теорему Піфагора ширше, ніж за програмою середньоі школи , навела приклади деяких доведень теореми і її наслідків , узагальнення цієї теореми . Тут розглянуто мною також теореми Чеви, Менелая, Дезарга, Паппа, Паскаля, які не входять в основний курс шкільної геометрії, між тим вони прості , цікаві й використовуються при розв'язуванні досить складних задач, у тому числі конкурсних, олімпіадних.
РОЗДІЛ І
ТЕОРЕМА ПІФАГОРА
1.1. Теорема Піфагора і обернена до неї
Піфагор Самоський (бл. 580—500 до н. е.) народився у Стародавній Греції на острові Самосі у багатій купецькій сім'ї. Здобув добру освіту, запозичив багато знань з математики Єгипту і Вавилона. Він займався музикою, гімнастикою, був навіть переможцем на Олімпійських іграх. У місті Кротоні (грецькій колонії на півдні Італії) Піфагор створив свою школу, яка діяла майже тридцять років і здобула 'велику популярність, головним чином досягненнями в галузі математики і астрономії.
Піфагору приписують винайдення теореми про співвідношення між сторонами прямокутного трикутника, хоча ця теорема або її частинні випадки були відомі в Єгипті, Вавилоні, Китаї. Найімовірніше, що йому належить доведення теореми, яка носить його ім'я. Піфагорійці вивчали прогресії і проекції, подібність фігур та ін. Важливим відкриттям Піфагора та його школи є відкриття несумірності сторони квадрата і його діагоналі, що було початком винайдення ірраціональних чисел. Піфагор одним з перших вважав, що Земля має форму кулі і є центром Всесвіту, що Сонце, Місяць і планети мають власний рух і т. ін.
Піфагор загинув, коли йому було майже 90 років.
 Теорема
Піфагора. У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі,
дорівнює сумі площ квадратів, побудованих на катетах.
Теорема
Піфагора. У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі,
дорівнює сумі площ квадратів, побудованих на катетах.
Дано: ![]()
Довести: ![]() .
.
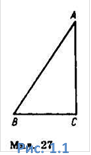
Доведення. Позначимо АВ = с, ВС = а, АС = b (Рис. 1.1).
Побудуємо два
рівні квадрати MNPQ і M1N1P1Q1,
(Рис. 1.2), кожна сторона яких дорівнює сумі катетів ![]() . Наприклад,
. Наприклад,
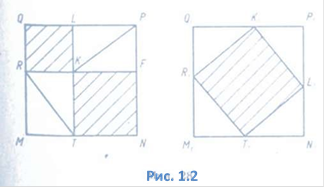 MN = МТ + TN = а
+ b. Розіб'ємо квадрат MNPQ на чотири трикутники, що дорівнюють трикутнику
ABC за двома катетами
MN = МТ + TN = а
+ b. Розіб'ємо квадрат MNPQ на чотири трикутники, що дорівнюють трикутнику
ABC за двома катетами
(МТ = RK = LK = PF = а і
RM = КТ = KF = LP = b), та два квадрати QRKL і TNFK, у яких QR = a,
TN = b, a квадрат M1N1P1Q1 — на чотири трикутники, що дорівнюють трикутнику
ABC також за двома катетами (М1Т1=
N1L1= = Р1K1 = Q1R1=
а і T1N1= L1P1 = К1Q1=
R1М1 = b), та квадрат T1L1K1R1.
Чотирикутник T1L1K1R1 — квадрат,
кожна його сторона дорівнює гіпотенузі трикутника ABC і кути прямі (![]() R1K1L1=
180° — (
R1K1L1=
180° — (![]() R1К1Q1+
R1К1Q1+![]() Р1K1L1) =
90°). Отже,
Р1K1L1) =
90°). Отже,
сума площ квадратів QRKL і TNFK, побудованих на катетах, дорівнює площі квадрата MNPQ без суми площ чотирьох рівних трикутників, а площа квадрата T1L1K1R1, побудованого на гіпотенузі, дорівнює площі квадрата M1N1P1Q1, який дорівнює квадрату MNPQ, без суми площ чотирьох таких самих трикутників.
Отже, ![]() . Теорему доведено.
. Теорему доведено.
Таке доведення теореми приписують самому Піфагору. Природно виникає запитання, чи завжди проти найбільшої сторони трикутника лежить прямий кут,
якщо виконується умова ![]() , де а, b, с — довжини
сторін трикутника.
, де а, b, с — довжини
сторін трикутника.
 Чи справедлива
теорема, обернена до піфагорової? Виявляється, що справедлива. Обернена
теорема. Якщо сума площ квадратів, побудованих на двох сторонах трикутника,
дорівнює площі квадрата, побудованого на третій стороні, то цей трикутник
прямокутний.
Чи справедлива
теорема, обернена до піфагорової? Виявляється, що справедлива. Обернена
теорема. Якщо сума площ квадратів, побудованих на двох сторонах трикутника,
дорівнює площі квадрата, побудованого на третій стороні, то цей трикутник
прямокутний.
Дано: ![]() .
.
Довести: ![]() АСВ = 90°.
АСВ = 90°.
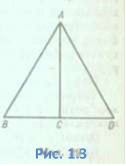
Доведення. Побудуємо CD ![]() АС у точці
С (Рис. 1.3) і на ньому відкладемо відрізок CD = ВС. Сполучивши А і D,
дістанемо прямокутний трикутник ACD. У трикутнику ACD AD2 = АС2
+ CD2 за теоремою Піфагора. За умовою АВ2 = АС2
+ ВС2.
АС у точці
С (Рис. 1.3) і на ньому відкладемо відрізок CD = ВС. Сполучивши А і D,
дістанемо прямокутний трикутник ACD. У трикутнику ACD AD2 = АС2
+ CD2 за теоремою Піфагора. За умовою АВ2 = АС2
+ ВС2.
Порівнюючи AD2
і АВ2 і враховуючи, що CD = ВС, маємо: AD = АВ. Отже, ![]() ABC =
ABC = ![]() ADC, а тому
ADC, а тому ![]() ACB ==
ACB == ![]() ACD = 90°.
Теорему доведено.
ACD = 90°.
Теорему доведено.
За два тисячоліття до нашої ери, ще до Піфагора, єгипетські землеміри будували прямий кут, встромивши кілки у землю і натягнувши у формі трикутника мотузку з вузлами на відстані 3, 4 і 5 одиниць так, щоб вузли співпали з кілками. Такий трикутник називають «єгипетським», або «піфагоровим». У ньому 52= З2 +42, а кут, який лежить проти найбільшої сторони, прямий.
Мабуть, роздумуючи над «єгипетським» трикутником, Піфагор почав шукати й інші прямокутні трикутники з цілочисло вими сторонами. Прямокутні трикутники, у яких довжини всі сторін виражаються цілими числами, називаються піфагоровими трикутниками. В давнину піфагоровим трикутникам надавали особливого значення, їм інколи приписували магічні властивості. Тепер відомо, що множина піфагорових трикутників нескінченна і є формули для визначення будь-якого з них.
Теорема Піфагора протягом багатьох століть була поштовхом до цікавих досліджень у геометрії. За теоремою Піфагора можна встановити метричні співвідношення між елементами не тільки прямокутного трикутника, а й інших фігур, які мають широке застосування. Наведемо приклади.
Задача 1.1. Доведіть, що в довільному трикутнику квадрат сторони, яка лежить проти тупого кута, дорівнює сумі квадратів двох інших сторін, доданій до подвоєного добутку однієї з цих сторін на проекцію другої сторони на першу.
Дано: ![]() ABC,
ABC, ![]() ACB > 90°. Довести:
ACB > 90°. Довести:
АВ2 = АС2 + ВС2 + 2ВС • DC.
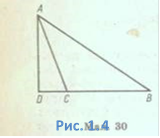 Доведення.
Проведемо висоту AD з вершини А (Рис. 1.4). За теоремою Піфагора з
Доведення.
Проведемо висоту AD з вершини А (Рис. 1.4). За теоремою Піфагора з ![]() ADB:
ADB:
АВ2
= AD2 + BD2, з ![]() ADC: АС2 =AD2+ DC2.
Віднімаючи ці рівності почленно, дістанемо: АВ2 - АС2 =
BD2- DC2.
ADC: АС2 =AD2+ DC2.
Віднімаючи ці рівності почленно, дістанемо: АВ2 - АС2 =
BD2- DC2.
Врахувавши, що BD = ВС + DC,
матимемо АВ2 = АС2 + ВС2 + 2ВС • DC.
Задача 1.2. Доведіть, що в будь-якому трикутнику квадрат сторони, яка лежить проти гострого кута, дорівнює сумі квадратів двох інших сторін без подвоєного добутку однієї з цих сторін на проекцію другої сторони на першу.
Дано: ![]() ABC,
ABC, ![]() ACB < 90°.
ACB < 90°.
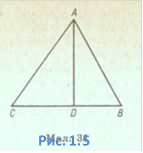 Довести: АВ2 = АС2 + ВС2
— 2ВС • CD.
Довести: АВ2 = АС2 + ВС2
— 2ВС • CD.
Доведення. Проведемо висоту AD з вершини А
(Рис. 1.5). Застосувавши теорему Піфагора до прямокутних трикутників ADC і ADB, дістанемо: АВ2 = BD2 + AD2, АС2 =
CD2 + AD2. Віднявши ці дві рівності почленно і врахувавши, що BD =ВС - CD, матимемо:
АВ2 = АС2 + ВС2 — 2ВС • CD.
Задача 1.3. Доведіть, що в будь-якому паралелограмі сума квадратів діагоналей дорівнює сумі квадратів сторін.
Дано: ABCD — паралелограм.
Довести: АС2 + BD2 = АВ2 + ВС2 + CD2 + AD2.
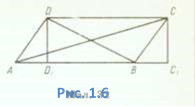 Доведення. Відомо, що в
паралелограмі протилежні кути рівні, кожна діагональ розбиває його на два рівні
трикутники, сума внутрішніх кутів, які прилягають до однієї сторони, дорівнює
180°. Тому,
Доведення. Відомо, що в
паралелограмі протилежні кути рівні, кожна діагональ розбиває його на два рівні
трикутники, сума внутрішніх кутів, які прилягають до однієї сторони, дорівнює
180°. Тому,
якщо сторона АС трикутника ABC (Рис.1.6)
лежить проти тупого кута, то сторона BD трикутника ABD лежить проти гострого
кута. З ![]() ABC і
ABC і ![]() ABD маємо: АС2 = АВ2 + ВС2
+ 2АВ • ВС, BD2 = AD2 + АВ2 — 2АВ • AD.
ABD маємо: АС2 = АВ2 + ВС2
+ 2АВ • ВС, BD2 = AD2 + АВ2 — 2АВ • AD.
Додавши ці дві рівності почленно і врахувавши, що ВС1= AD1 і АВ = DC, дістанемо: АС2 + BD2 = АВ2 + ВС2 + CD2 + AD2.
1.2. Різні доведення теореми Піфагора
Теоремою Піфагора займалося багато математиків протягом багатьох століть. Нині відомо понад 300 доведень цієї теореми. Залежно від способу доведення інколи змінюється і формулювання самої теореми. Наприклад, у шкільному підручнику вона звучить так: «У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів», а доведення її проводиться з використанням косинуса кута.
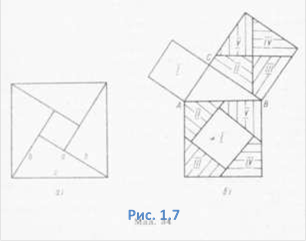
 Чимало доведень теореми
Піфагора базуються на рівновеликості і рівноскладеності геометричних фігур. Для
цього на гіпотенузі і катетах даного прямокутного трикутника будують фігури,
певним чином розміщені, порівнюючи і зіставляючи які, переконуються у правильності
теореми.
Чимало доведень теореми
Піфагора базуються на рівновеликості і рівноскладеності геометричних фігур. Для
цього на гіпотенузі і катетах даного прямокутного трикутника будують фігури,
певним чином розміщені, порівнюючи і зіставляючи які, переконуються у правильності
теореми.
На рисунку 1.7 наведено приклади
таких доведень. Теорему Піфагора для випадку
рівнобедреного прямокутного трикутника іноді жартома
Рис. 1.8
називають «піфагоровими штанами» (Рис. 1.8). У Франції і Німеччині теорему
Піфагора називали «ослячим мостом».
1.3. Узагальнення теореми Піфагора
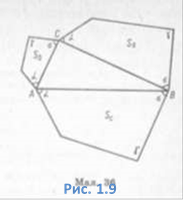 Теорема Піфагора має
місце, якщо замість квадратів на сторонах прямокутного трикутника побудувати
довільні подібні між собою фігури (Рис.
Теорема Піфагора має
місце, якщо замість квадратів на сторонах прямокутного трикутника побудувати
довільні подібні між собою фігури (Рис.
1.9). Позначимо площі подібних фігур,
побудованих на катетах, Sa і Sb, а на гіпотенузі — Sc.
Доведемо, що Sa + Sb = Sc.
Доведення. З того, що площі подібних фігур відносяться, як квадрати відповідних
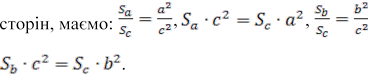 ,
,
Якщо додати виведені рівності, знайдемо:
![]() ).
Врахувавши, що
).
Врахувавши, що
![]() =
, дістанемо: = .
=
, дістанемо: = .
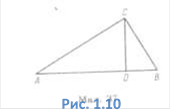 Отже, площа фігури,
побудованої на гіпотенузі прямокутного трикутника, дорівнює сумі площ подібних
їй фігур, побудованих на катетах цього трикутника. У справедливості цього
твердження можна переконатися, виходячи з таких міркувань. Якщо в прямокутному
трикутнику ABC провести висоту CD з вершини прямого кута С на гіпотенузу АВ, то
матимемо прямокутні, подібні між собою, трикутники: ABC, BCD і ADC, побудовані
на
Отже, площа фігури,
побудованої на гіпотенузі прямокутного трикутника, дорівнює сумі площ подібних
їй фігур, побудованих на катетах цього трикутника. У справедливості цього
твердження можна переконатися, виходячи з таких міркувань. Якщо в прямокутному
трикутнику ABC провести висоту CD з вершини прямого кута С на гіпотенузу АВ, то
матимемо прямокутні, подібні між собою, трикутники: ABC, BCD і ADC, побудовані
на
гіпотенузі АВ і катетах ВС і АС відповідно. З рисунка 1.10 видно, що площа трикутника ABC дорівнює сумі площ трикутників ACD і BCD.
РОЗДІЛ 2 ТЕОРЕМИ ЧЕВИ І МЕНЕЛАЯ
2.1. Теорема Чеви
Чева Джованні (1648—1734) — італійський інженер-гідравлік і геометр. Працював інженером міста Мантуя. Основною його заслугою є створення вчення про січні, яке поклало початок новій синтетичній геометрії. Воно викладене в його праці «Про прямі, що взаємно перетинаються» (1678). У цій книжці властивості прямолінійних фігур розглядаються через властивості центра інерції системи точок.
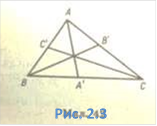
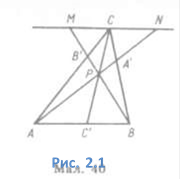 Теорема Чеви.
Нехай точки А', В', С' лежать на прямих, які визначаються сторонами трикутника
ABC. Для того, щоб прямі АА', ВВ', СС' перетиналися в одній точці або були
паралельними, необхідно і достатньо, щоб
Теорема Чеви.
Нехай точки А', В', С' лежать на прямих, які визначаються сторонами трикутника
ABC. Для того, щоб прямі АА', ВВ', СС' перетиналися в одній точці або були
паралельними, необхідно і достатньо, щоб
![]() 1.
(2.1)
1.
(2.1)
Доведення. Необхідність, а) Нехай у трикутнику ABC (Рис. 2.1) АА', ВВ',СС' перетинаються в одній точці Р. Через вершину С проведемо пряму MN паралельно стороні АВ трикутника ABC (Рис. 2.1). З подібності трикутників АС'Р і CPN, ВС'Р і СМР маємо:
![]() (2.2)
(2.2)
З подібності трикутників ABA' і A'CN, ABB' і В'СМ знаходимо відповідно:
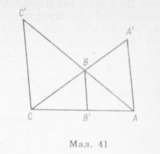
![]() (2.3),
(2.3), ![]() (2.4).
(2.4).
Перемножимо рівності (2.2), (2.3), (2.4), дістанемо
![]() 1.
1.
Зауважимо, що відрізки прямої (паралельних прямих) Рис. 2.2
мають однакові знаки, якщо вони однаково напрямлені, різні, якщо вони протилежно напрямлені.
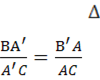 б) Нехай у
ABC АА' ВВ' СС' (Рис. 2.2). За теоремою Фалеса маємо:
б) Нехай у
ABC АА' ВВ' СС' (Рис. 2.2). За теоремою Фалеса маємо:
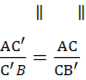 (2.5), (2.6),
(2.5), (2.6), ![]() (2.7).
(2.7).
Перемножимо рівності (2.5), (2.6), (2.7), дістанемо: АС ![]() 1, що
1, що
треба довести.
Достатність. Якщо в ![]() ABC
ABC ![]() 1,
то прямі АА', ВВ', СС'
1,
то прямі АА', ВВ', СС'
перетинаються в одній точці або паралельні.
Припустимо, що
АА' ![]() ВВ'
= Р і Р
ВВ'
= Р і Р ![]() СС'. Проведемо пряму СРС1. За
доведеним вище матимемо:
СС'. Проведемо пряму СРС1. За
доведеним вище матимемо:
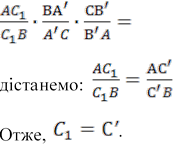 1. Порівнюючи
цю рівність з умовою
1. Порівнюючи
цю рівність з умовою ![]() 1,
1,
.
Якщо припустити, що АА' || ВВ', то легко довести, що и пряма СС' їм паралельна. Прямі, які виходять з вершин трикутника і перетинаються в одній точці або паралельні, називаються прямими Чеви, або чевіанами.
Задача 2.1. Доведіть, що медіани трикутника ABC перетинаються, в одній точці.
Доведення. Якщо АА', ВВ', СС' — медіани, то АС'= С'В,
ВА' = А'С, СВ' = В'А. Тому ![]() 1. За теоремою
1. За теоремою
Чеви прямі АА', ВВ', СС' перетинаються в одній точці.
Задача 2.2. Доведіть, що бісектриси внутрішніх кутів трикутника ABC перетинаються в одній точці.
Доведення. Позначимо ВС = а, АС = b,
АВ = с (Рис. 2.3). За властивостями бісектриси маємо:
![]() .
.
Перемноживши ці рівності, знаходимо:
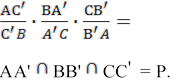 1.За теоремою Чеви
1.За теоремою Чеви
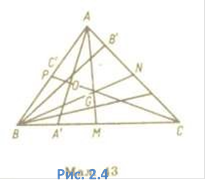 Задача 2.3.
Всередині трикутника ABC знайдіть точку О, щоб добуток відрізків АВ', ВС', СА'
був найбільшим (А', В', С' — точки перетину чевіан, які проходять через точку
О, з сторонами трикутника). Розв'язання. У трикутнику ABC (Рис. 2.4) проведемо
медіани АМ, BN, CP, які перетинаються в точці G. Якщо врахувати, що середнє
геометричне не більше за середнє арифметичне, то
Задача 2.3.
Всередині трикутника ABC знайдіть точку О, щоб добуток відрізків АВ', ВС', СА'
був найбільшим (А', В', С' — точки перетину чевіан, які проходять через точку
О, з сторонами трикутника). Розв'язання. У трикутнику ABC (Рис. 2.4) проведемо
медіани АМ, BN, CP, які перетинаються в точці G. Якщо врахувати, що середнє
геометричне не більше за середнє арифметичне, то
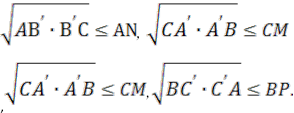
Піднесемо обидві частини нерівностей до квадрата і перемножимо:
![]() .
.
За теоремою Чеви маємо, що
![]() .
.
Отже,
![]()
З цієї нерівності
видно, що добуток відрізків ![]() найбільший, якщо нерівність стане рівністю,
тобто коли точки А', В', С' збігаються з точками М, N,
найбільший, якщо нерівність стане рівністю,
тобто коли точки А', В', С' збігаються з точками М, N,
Р, отже, чевіани збігаються з медіанами.
2.2. Теорема Менелая і обернена до неї
Менелай Александрійський (І ст.) — давньогрецький математик і астроном, відомий своїми працями в галузі сферичної тригонометрії. Збереглося шість його книг про обчислення хорд і три книги «Сферіки». Теорему Менелая для трикутника спочатку було доведено для великих кіл на сфері.
Теорема Менелая.
Якщо сторони АВ, ВС, АС трикутника ABC, або їх продовження, перетинаються
прямою в точках ![]() відповідно, то
відповідно, то
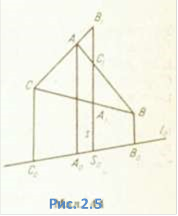
![]()
Доведення.
Проведемо довільну пряму ![]() у площині трикутника ABC (Рис. 2.5). З вершин
А, В, С
у площині трикутника ABC (Рис. 2.5). З вершин
А, В, С
трикутника ABC проведемо прямі ![]()
паралельні трансверсалі s, які
перетинають пряму ![]() у точках
у точках ![]() . Пряма s перетинає пряму
. Пряма s перетинає пряму ![]() точці
точці
 . За теоремою
Фалеса будемо мати, що
. За теоремою
Фалеса будемо мати, що
Якщо перемножити ці рівності почленно і
врахувати орієнтацію відрізків, дістанемо: ![]()
Теорему доведено.
Цей висновок теореми можна записати у такому вигляді:
(ABC1) (ВСА1) (САВ1) = 1.
Де кожний вираз у дужках є простим відношенням трьох точок. З цього виразу приходимо до висновку, що трансверсаль може перетинати дві сторони трикутника і продовження третьої сторони або продовження всіх трьох сторін. У першому випадку два простих відношення від'ємні, а одне додатне, а в другому — всі три відношення додатні.
Теорему Менелая можна сформулювати так: Якщо пряма перетинає сторони трикутника або їх продовження, то добуток трьох відрізків, які не мають спільних кінців, дорівнює добутку трьох інших таких самих відрізків.
Обернена теорема
Менелая. Якщо точки ![]() розміщені
на сторонах (або їх продовженні) трикутника ABC так, що (ABC1) (ВСА1)
(САВ1) = 1, то вони лежать на одній прямій.
розміщені
на сторонах (або їх продовженні) трикутника ABC так, що (ABC1) (ВСА1)
(САВ1) = 1, то вони лежать на одній прямій.
Доведення. Припустимо, що пряма ![]() перетинає
сторони ВС і АВ трикутника в точках
перетинає
сторони ВС і АВ трикутника в точках ![]() , а точка
, а точка ![]() цій прямій не належить.
Нехай пряма
цій прямій не належить.
Нехай пряма ![]() перетинає продовження сторони СА в точці В'.
За теоремою Менелая для точок C1, А1, В' виконується
умова (ABC1) (ВСА1) (САВ' ) = 1. (2.2)
перетинає продовження сторони СА в точці В'.
За теоремою Менелая для точок C1, А1, В' виконується
умова (ABC1) (ВСА1) (САВ' ) = 1. (2.2)
За умовою теореми
(ABC1) (ВСА1) (САВ1) = 1. (2.3)
Поділивши рівність (2.2) на рівність (2.3), дістанемо
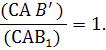
Отже, точки В' і В1 збігаються. Теорему доведено.
РОЗДІЛ 3 ТЕОРЕМИ КАРНО І ДЕЗАРГА
3.1. Теорема Карно
Карно Лазар (1753—1823) — французький громадський діяч і математик. Математичні праці з аналізу і геометрії. У геометричних працях виступав як попередник засновників проективної геометрії. Узагальнив теорему Менелая. Теорема Карно. Якщо сторони многокутника або їх продовження перетнути прямою, то добуток відрізків сторін, які не мають спільних кінців, дорівнює добуткові решти відрізків.
3.2. Теорема Дезарга
Дезарг Жірар (1591 —1662) — французький математик, заклав основи проективної і нарисної геометрії. Був архітектором і військовим інженером. У своїх дослідженнях систематично застосовував перспективне зображення. Його твір про конічні перерізи має загальний проективно-геометричний характер. Важливість ідей Дезарга зрозуміли тільки найвизначніші математики того часу — Р. Декарт, П. Ферма, Б. Паскаль.
Теорема Дезарга. Якщо прямі АА1,
ВВ1, СС1, які сполучають відповідні вершини трикутників
ABC і ![]() ,
перетинаються в одній точці, то відповідні їх сторони перетинаються в точках
,
перетинаються в одній точці, то відповідні їх сторони перетинаються в точках ![]() які лежать на одній
прямій, якщо серед відповідних сторін немає паралельних.
які лежать на одній
прямій, якщо серед відповідних сторін немає паралельних.
![]()
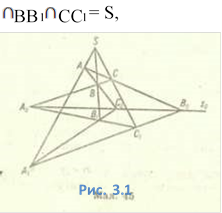
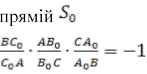 Доведення.
Нехай у ABC і маємо: АА1
Доведення.
Нехай у ABC і маємо: АА1
АВ![]() ,
,
AC ![]() . Якщо скористатися теоремою
. Якщо скористатися теоремою
Менелая, то, щоб точки ![]() лежали на
лежали на
, варто довести, що
.
Розглянемо трикутник ABS (Рис. 3.1), який перетинає пряма ![]() ,
матимемо
,
матимемо
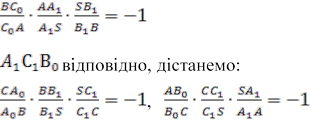 , а з
трикутників BCS і ACS, які перетинають прямі
, а з
трикутників BCS і ACS, які перетинають прямі ![]() і
і
.
Якщо перемножимо ці рівності, то знайдемо:
Теорему доведено. Точка S називається точкою Дезарга, a — прямою Дезарга.
Обернена теорема Дезарга. Якщо відповідні
сторони АВ і , ВС і ![]() , АС і
, АС і
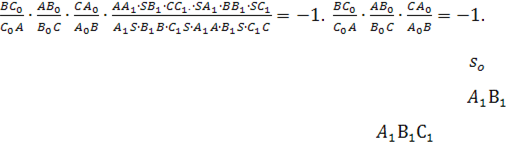
![]() (або їх
продовження) трикутників ABC і перетинаються в точках
(або їх
продовження) трикутників ABC і перетинаються в точках ![]() які лежать на
одній прямій, то прямі АА1, ВВ1, СС1, які
сполучають
які лежать на
одній прямій, то прямі АА1, ВВ1, СС1, які
сполучають
від![]() повідні вершини, перетинаються в одній точці S,
якщо вони не паралельні.
повідні вершини, перетинаються в одній точці S,
якщо вони не паралельні.
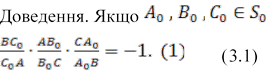 , то за теоремою Менелая
виконується умова
, то за теоремою Менелая
виконується умова
Припустимо, що прямі АА1 і ВВ1 перетинаються в точці S, а пряма СС1 через цю точку не проходить. За теоремою Менелая існує пряма С1С2, яка проходить через точку S і виконується умова
![]() (3.2)
(3.2)
Порівнюючи (3.1) і (3.2), знаходимо ![]() , звідки видно, що
, звідки видно, що ![]() .
.
. Теорему доведено.
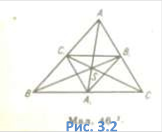 Задача 3.1.
Доведіть, що медіани трикутника ABC перетинаються в одній точці.
Задача 3.1.
Доведіть, що медіани трикутника ABC перетинаються в одній точці.
Розв'язання. Побудуємо трикутник ![]() ,
вершинами якого є основи
,
вершинами якого є основи ![]() медіан трикутника ABC. Дістанемо два
трикутники ABC і
медіан трикутника ABC. Дістанемо два
трикутники ABC і ![]() , (Рис. 3.2), у яких відповідні сторони АВ і
, (Рис. 3.2), у яких відповідні сторони АВ і ![]() , ВС і
, ВС і ![]() , АС і
, АС і ![]() паралельні,
а медіани АА1,
паралельні,
а медіани АА1,
ВВ1, СС1 перетинаються в одній точці S.
Задача 3.2. Знайдіть напрям між береговою А і річковою С опорами моста, який проектується.
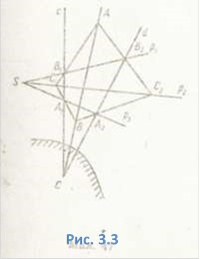 Розв'язання.
Використаємо теорему Дезарга. Для цього виберемо довільну точку S на березі,
через яку проведемо прямі
Розв'язання.
Використаємо теорему Дезарга. Для цього виберемо довільну точку S на березі,
через яку проведемо прямі ![]() . (Рис.
. (Рис.
3.3). Знайдемо точки ![]() перетину цих
перетину цих
прямих з прямими
с і d. Проведемо прямі АВ1 , АВ2, точки перетину яких з
прямою ![]() позначимо
відповідно С1 і C2, а точки перетину прямих С1А1
і C2A2 через В. Трикутники А1В1С1
і А2В2С2 відповідні, точка S — точка Дезарга,
пряма ABC — пряма Дезарга.
позначимо
відповідно С1 і C2, а точки перетину прямих С1А1
і C2A2 через В. Трикутники А1В1С1
і А2В2С2 відповідні, точка S — точка Дезарга,
пряма ABC — пряма Дезарга.
Отже, точки А і В визначають шуканий напрям ABC. Задача 3.3. На площині дано три прямі, які перетинаються в одній точці, і три точки. Побудуйте трикутник, вершини якого лежать на даних прямих, а сторони проходять через дані точки.
![]()
![]()
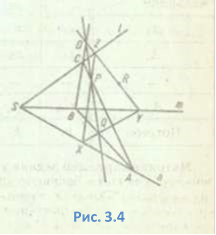 Розв'язання.
Нехай
Розв'язання.
Нехай ![]() =
S; Р, Q, R — дані точки. Треба побудувати
=
S; Р, Q, R — дані точки. Треба побудувати ![]() XYZ, щоб , і
Q ХУ, Р XZ, R
XYZ, щоб , і
Q ХУ, Р XZ, R ![]() YZ. Припустимо, що трикутник XYZ побудовано
(Рис. 3.4). Побудуємо трикутник ABC, вершини якого лежать ;на прямих , ,
і дві його сторони проходять через дані точки Р і Q. Використовуючи теорему
Дезарга, знаходимо, що точка S — дезаргова точка, пряма PQ — дезаргова пряма, а
трикутники XYZ і ABC — відповідні дезаргові трикутники.
YZ. Припустимо, що трикутник XYZ побудовано
(Рис. 3.4). Побудуємо трикутник ABC, вершини якого лежать ;на прямих , ,
і дві його сторони проходять через дані точки Р і Q. Використовуючи теорему
Дезарга, знаходимо, що точка S — дезаргова точка, пряма PQ — дезаргова пряма, а
трикутники XYZ і ABC — відповідні дезаргові трикутники.
Отже, вибравши
довільну точку А на прямій ![]() , проводимо АР і AQ, які визначать точки С і В.
Знаходимо точку D перетину сторони ВС з прямою PQ. Проводимо пряму DR, яка
визначить вершини Z і Y шуканого трикутника. Вершину X знаходимо як перетин
прямих ZP, YQ з прямою
, проводимо АР і AQ, які визначать точки С і В.
Знаходимо точку D перетину сторони ВС з прямою PQ. Проводимо пряму DR, яка
визначить вершини Z і Y шуканого трикутника. Вершину X знаходимо як перетин
прямих ZP, YQ з прямою ![]() . Побудований трикутник XYZ задовольняє задачу.
. Побудований трикутник XYZ задовольняє задачу.
РОЗДІЛ 4 ТЕОРЕМИ ПАСКАЛЯ 1 ПАППА
4.1. Теорема Паскаля
Паскаль Блез (1623—1662) — французький математик, фізик і філософ. Змалку захоплювався математикою, дванадцятирічним хлопчиком, потай від батька, розробив початки геометрії, прочитав книгу «Начала» Евкліда. Він займався арифметичними рядами, біноміальними коефіцієнтами, які утворював, використовуючи повну математичну індукцію. Великий внесок Паскаль зробив у розробку нескінченно малих та ін.
Теорема. Якщо, шестикутник АВСDЕF вписано в коло і протилежні сторони його АВ і DЕ, ВС і ЕF, СD і FА не паралельні, то точки перетину цих сторін лежать на одній прямій.
Доведення. Нехай Р, Q, R — точки перетину продовження сторін АВ, FЕ, СD, які утворюють трикутник РQR. (Рис. 4.1).
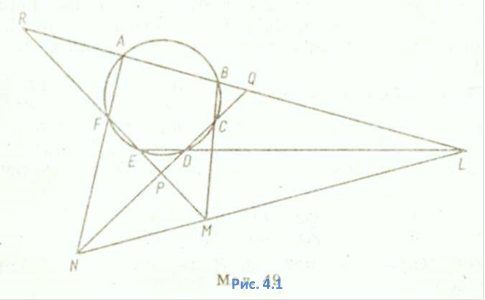
Якщо довести, що ![]() , то за теоремою Менелая точки L, М, N
, то за теоремою Менелая точки L, М, N
лежать на одній
прямій ![]() .
Розглядаючи трикутник РQR, який перетинають прямі LЕD, МСВ і NFA, відповідно
дістали рівності:
.
Розглядаючи трикутник РQR, який перетинають прямі LЕD, МСВ і NFA, відповідно
дістали рівності:
![]() .
.
Якщо перемножити ці рівності, то знайдемо:
![]()
Враховуючи, що
![]() ,
матимемо:
,
матимемо:
![]() яка означає, що точки L, М, N
лежать на одній прямій. Теорему
яка означає, що точки L, М, N
лежать на одній прямій. Теорему
доведено.
4.2. Теорема Паппа
Папп (III ст.) — давньогрецький математик. Найважливіша з праць Паппа — «Зібрання» у восьми книгах, в яких сумлінно викладені відомості з математики і деякі теореми самого Паппа.
![]() Теорема. Якщо на двох різних
прямих і міститься по три різних точки А, В, С і D, Е, F відповідно, то
точки Р, Q, R перетину сторін АЕ і ВF, АD і СF, ВD і СЕ лежать на одній прямій.
Теорема. Якщо на двох різних
прямих і міститься по три різних точки А, В, С і D, Е, F відповідно, то
точки Р, Q, R перетину сторін АЕ і ВF, АD і СF, ВD і СЕ лежать на одній прямій.
Дано: АЕСFВD — шестикутник, ![]() ,
,
A, B, C![]() .
.
Довести: ![]() .
.
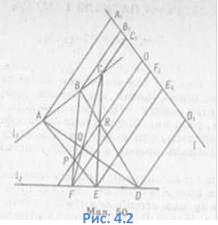 Доведення.
Проведемо довільну пряму
Доведення.
Проведемо довільну пряму ![]() , яка перетинає пряму РR в точці О (Рис. 4.2).
Далі проведемо прямі, паралельні прямій РR, які перетнуть пряму
, яка перетинає пряму РR в точці О (Рис. 4.2).
Далі проведемо прямі, паралельні прямій РR, які перетнуть пряму ![]() в точках D1,
Е1, F1, A1, В1, С1.
в точках D1,
Е1, F1, A1, В1, С1.
За теоремою Фалеса матимемо
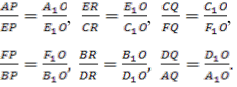
Перемножимо ці рівності і проведемо необхідні скорочення, дістанемо:
![]() За теоремою Карно
точки Р, Q, R лежать на одній
За теоремою Карно
точки Р, Q, R лежать на одній
прямій. Теорему доведено.
ВИСНОВКИ
Розв’язування задач складає суттєву сторону процесу навчання математиці:
рівень математичної підготовки в більшості визначається глибиною навиків у розв’язанні задач.
Ці обставини спонукають з особливою увагою відноситись до організації в середніх школах, гімназіях та ліцеях ретельно продуманих занять, які мають за мету надати учням не тільки теоретичні знання в області геометрії, але й навчити їх вільно застосовувати здобуті знання до розв’язання нестандартних задач середньої та підвищенної складності.
Останнім часом у варіантах вступних іспитів все частіше зустрічаються задачі, розв’язок яких суттєво спрощується за допомогою теорем Чеви та Менелая.
Робота присвячена вивченню теорем Чеви та Менелая на площині, доведенню нетривіальних наслідків цих теорем та розв’язанню задач за допомогою цих теорем.
Теорема Менелая має широке застосування при доведенні теорем (наприклад, теорем Дезарга, Паппа, Паскаля, Гаусса та інших) та розв’язанні задач. Теорема Менелая дозволяє знаходити відношення відрізків, а також доводити належність трьох точок одній прямій. Багато задач можна розв’язати кількома способами: традиційними і за допомогою теореми Менелая, при цьому останній спосіб розв’язання задач виявляється більш раціональним (розв’язок задачі займає всього кілька рядків). Зазначимо, що при розв’язуванні задач найскладнішою справою є пошук трикутника, до якого слід застосувати теорему Менелая.
Теореми Чеви використовується при розв’язуванні задач про трійки прямих, що проходять через одну точку, а також при доведенні теорем про перетин трійок прямих в одній точці.
Наведені в роботі задачі можуть бути використані при позакласній роботі з учнями (на заняттях гуртків, при проведенні математичних олімпіад, для індивідуальної роботи з найбільш здібними учнями).
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Бевз Г. П . Геометрія трикутника. К : Генеза , 2005 ,с. 49-52.-21.
2. Буник І. Теорема Менелая // Математика. – №15(315), квітень, 2005. – с.17
3. Егоров А. Теоремы Чевы и Менелая // КВАНТ, №3, 2004, с.35-38.
4. Зетель С.И. Новая геометрия треугольника. – М., – 1962. – С. 151.
5. Коксетер Г.С., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука, 1978. – 223 с.
6. Куланин Е. Об одной трудной геометрической задаче // КВАНТ, №7,1992.–с.4650
7. Орач Б. Теорема Менелая // КВАНТ, №3, 1991, с. 52-55.
8. Прасолов В.В. Задачи по планиметрии, ч.1. – М.: Наука, 1986. – 272 с.
9. Прасолов В.В. Задачи по планиметрии, ч.2. – М.: Наука, 1991. – 240 с.
10. Скопец З.А., Жаров В.А. Задачи и теоремы по геометрии (планиметрия). – М., 1962. – 162 с.
11. Шарыгин И. Ф. Теоремы Чевы и Менелая // КВАНТ, №11, 1976.
12. Шарыгин И.Ф. Задачи по геометрии: Планиметрия. – М.: Наука, 1986.
13. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы планиметрии. – М.: Наука, 1967.
14. Эрдниев Б., Манцаев Н. Теоремы Чевы и Менелая // КВАНТ, №3, 1990, с. 56-
59.


про публікацію авторської розробки
Додати розробку
