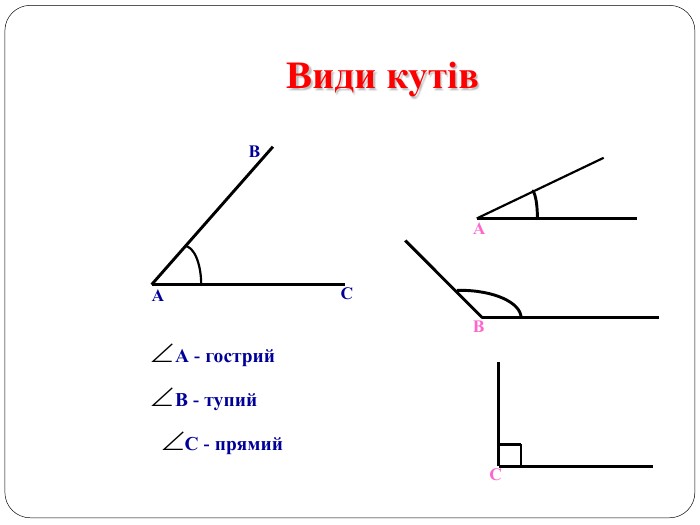
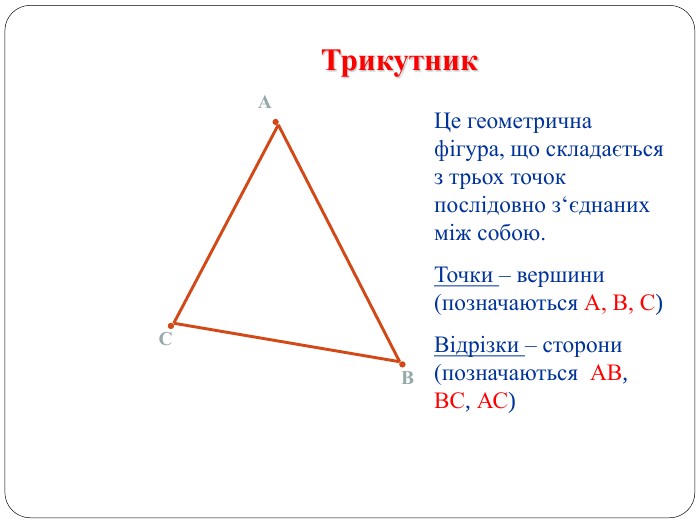
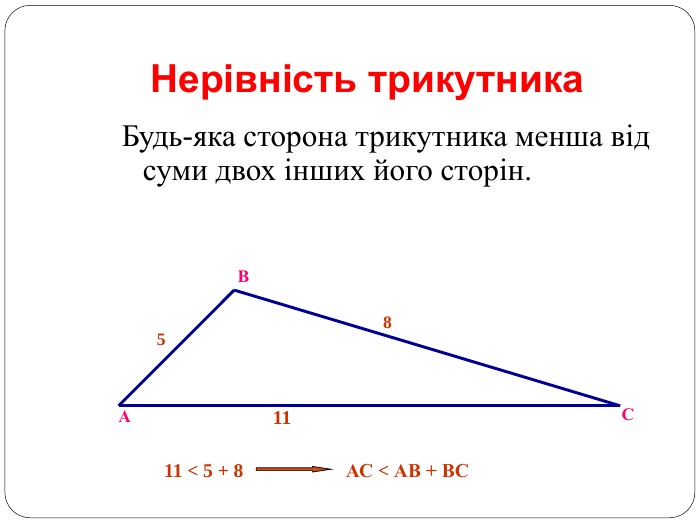
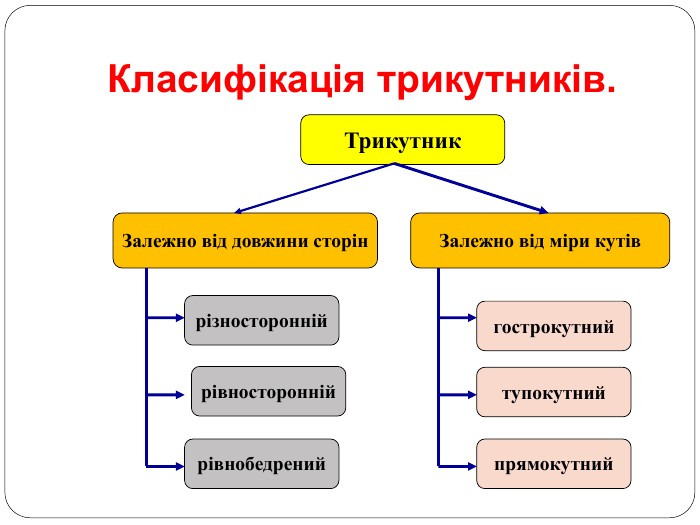
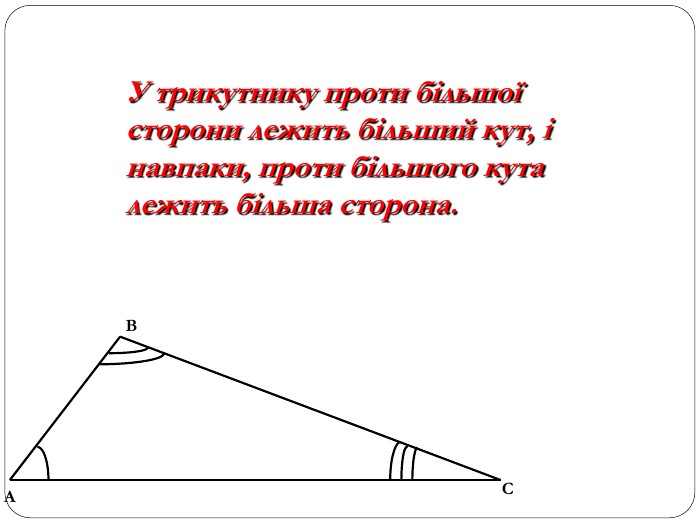
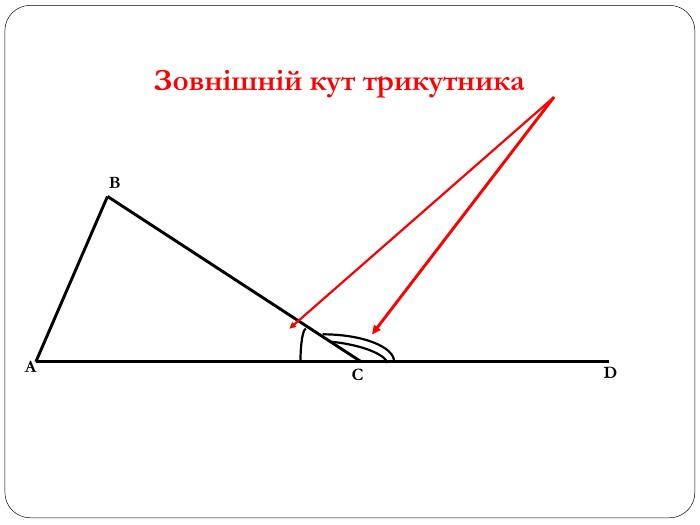
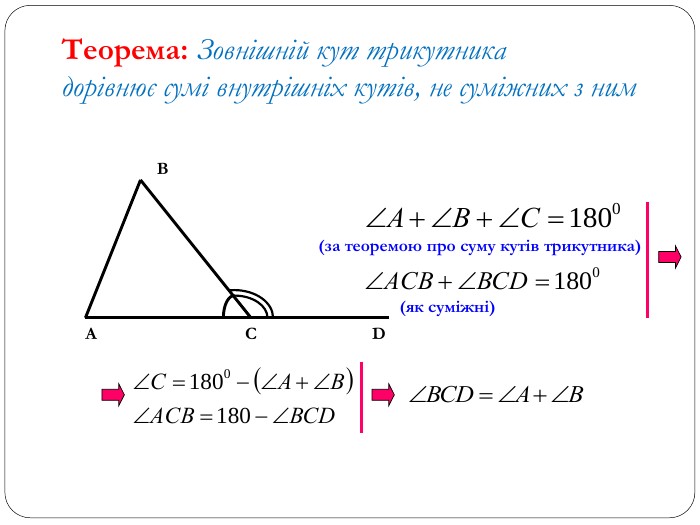
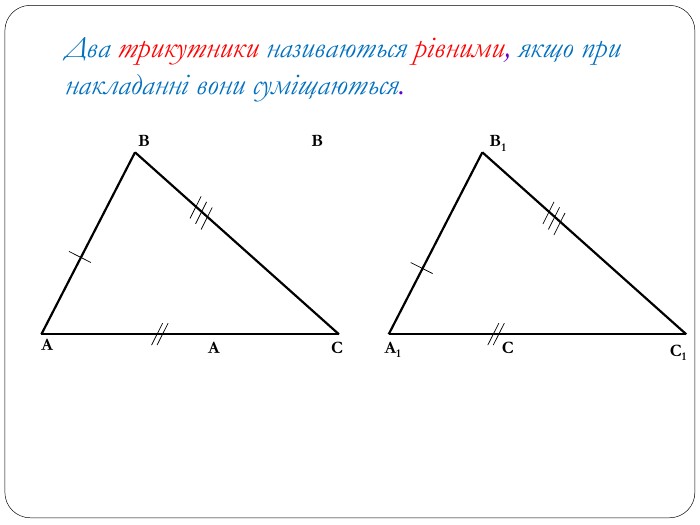
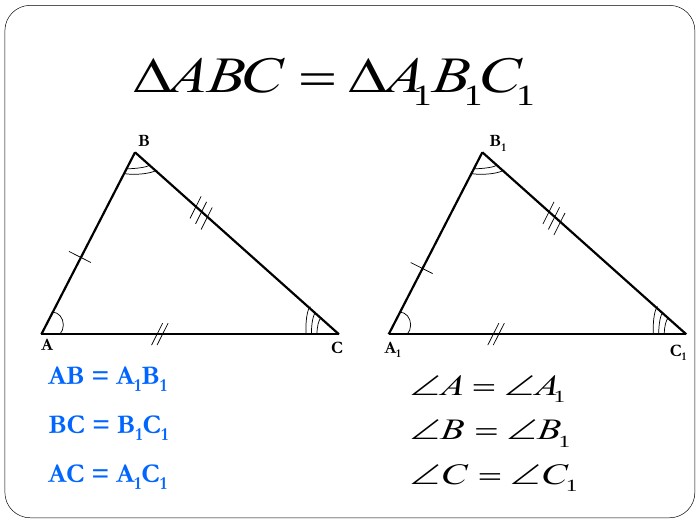
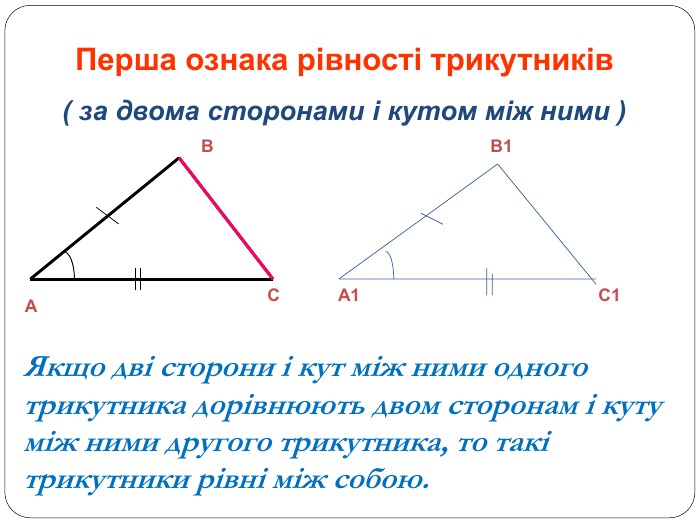
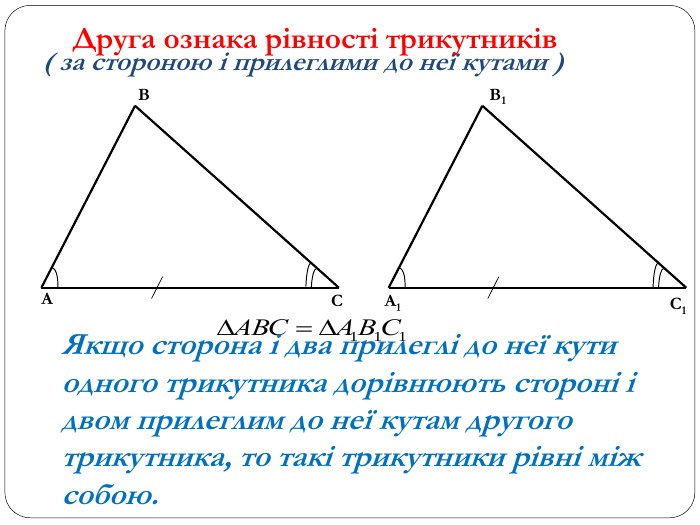
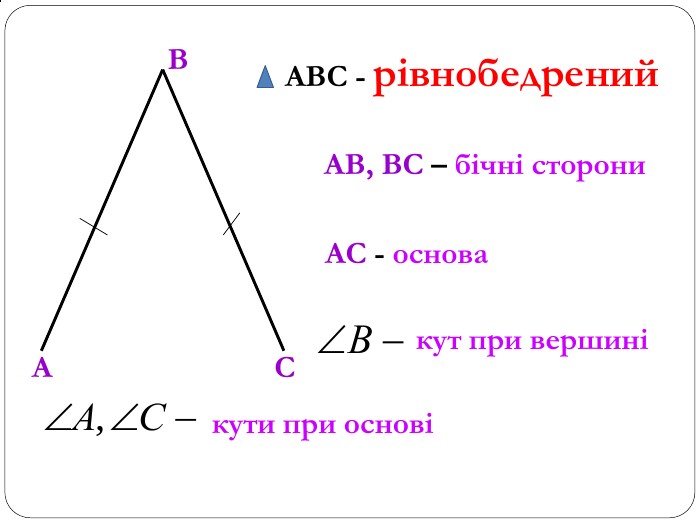
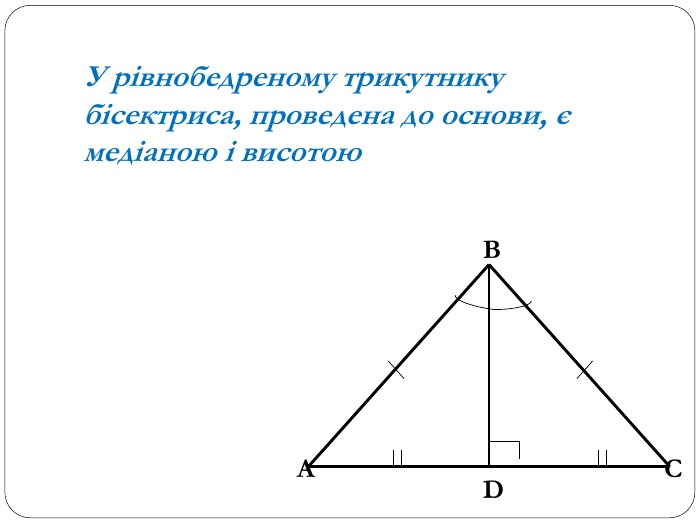
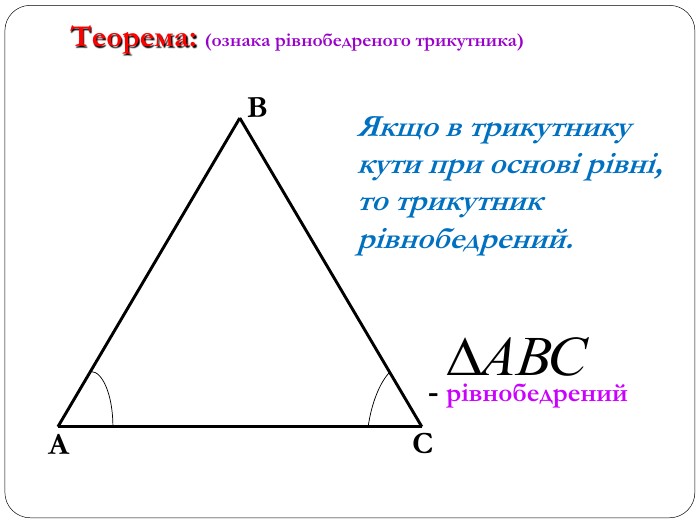
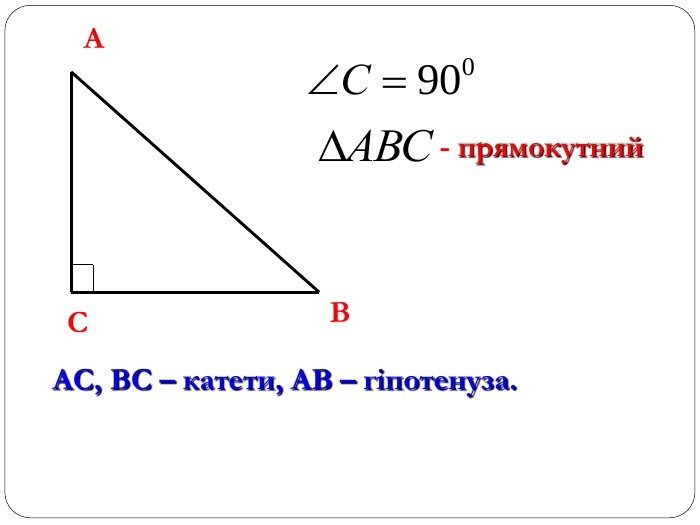
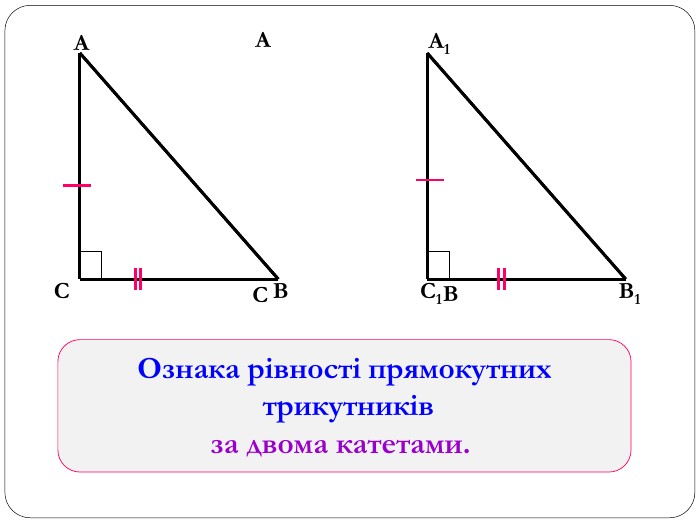
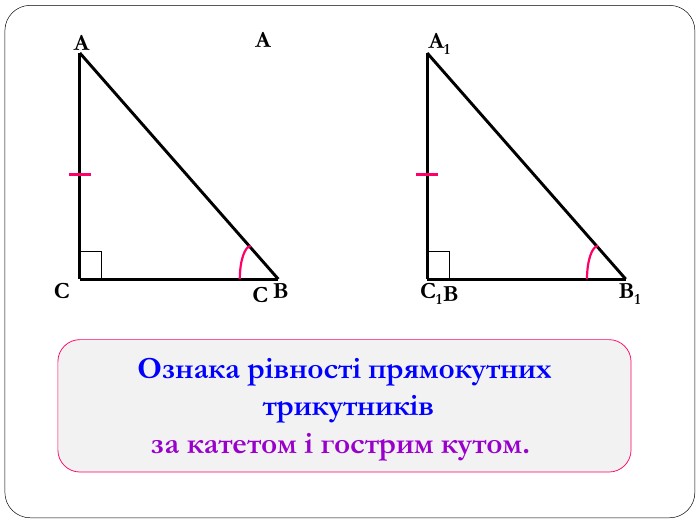
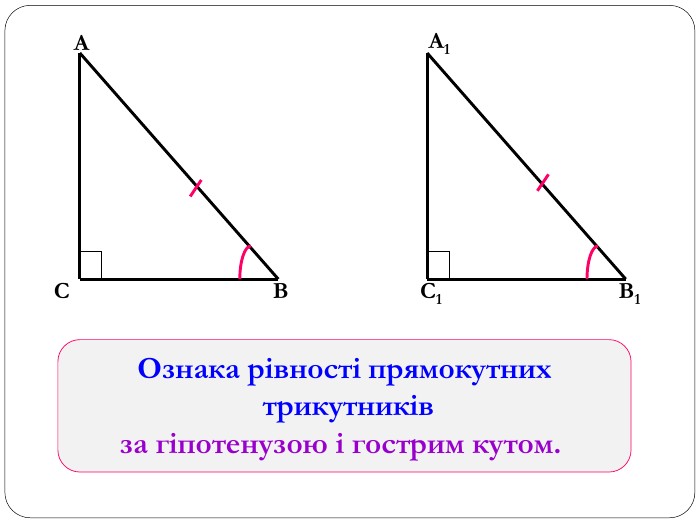
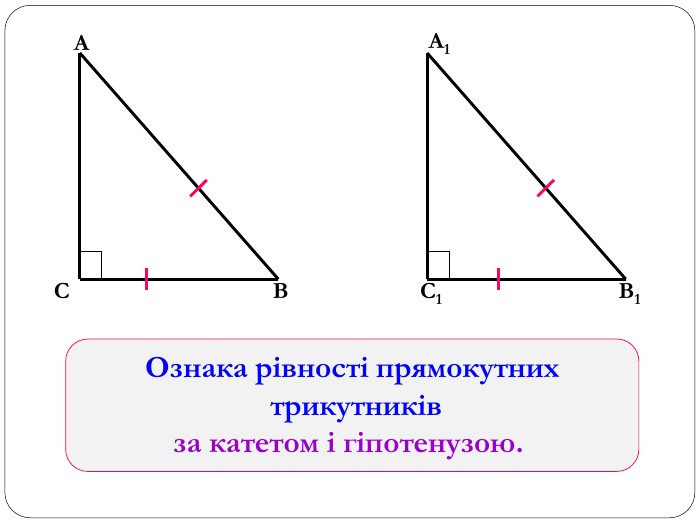
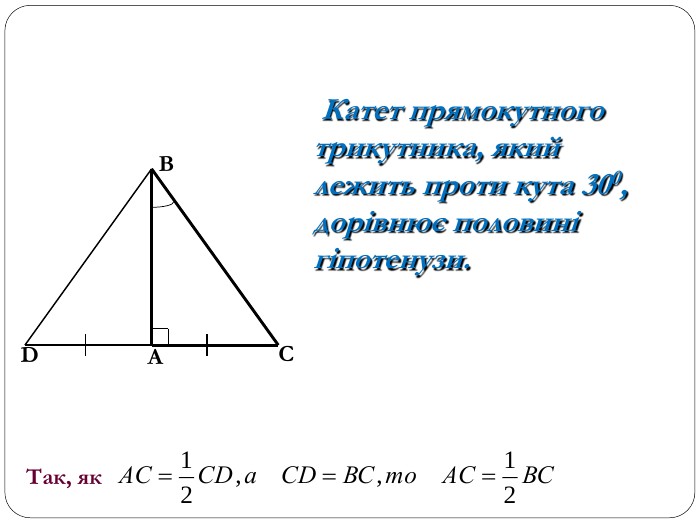
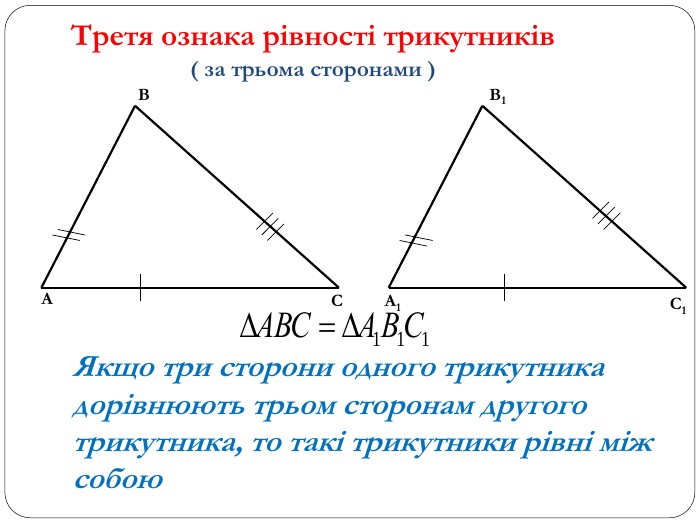
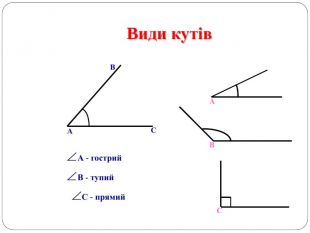
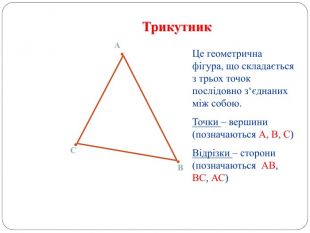
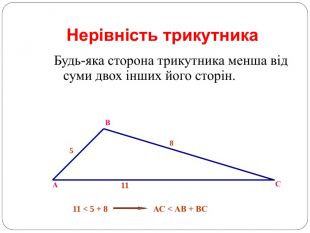
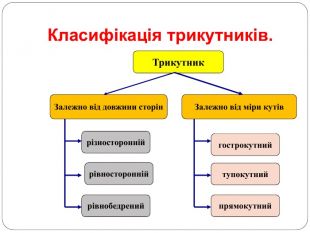
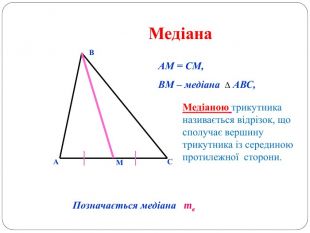
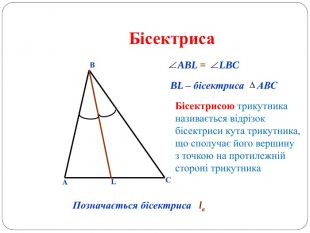
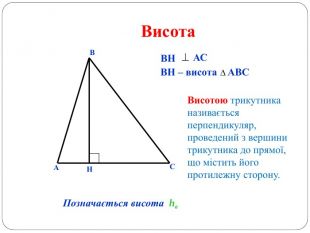
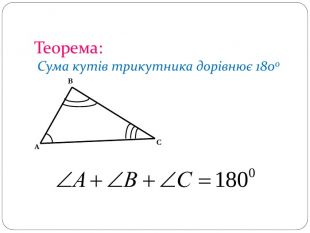
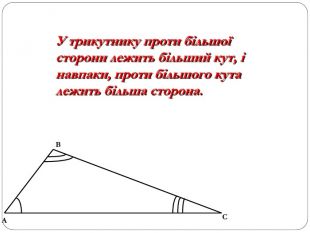
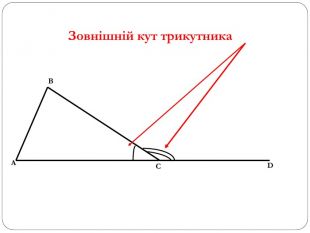
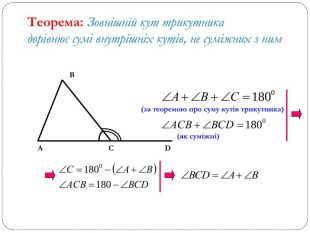
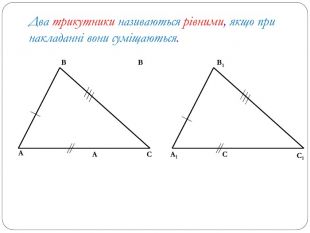
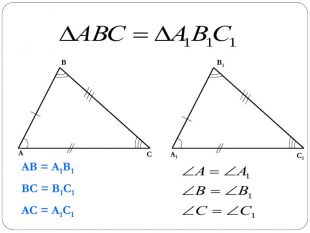
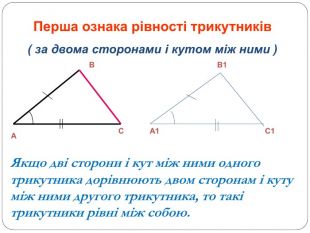
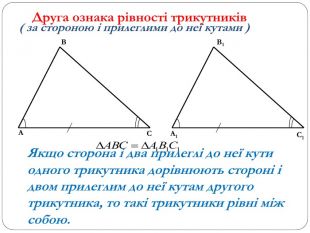
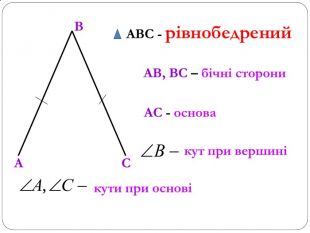
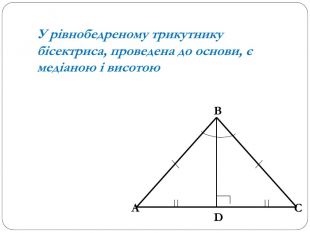
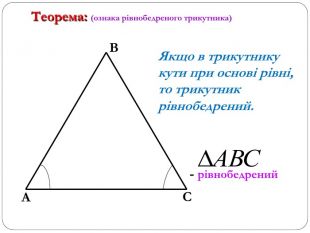
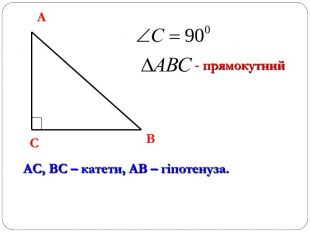
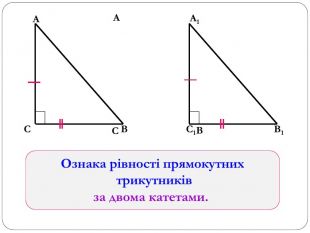
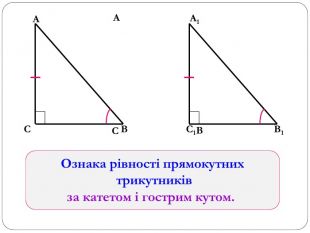
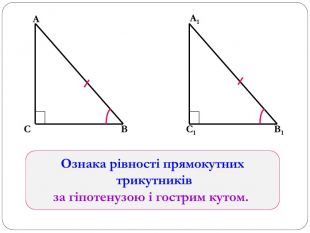
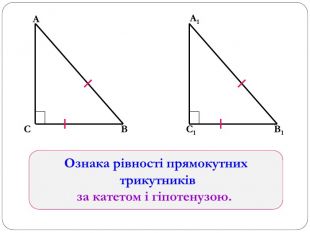
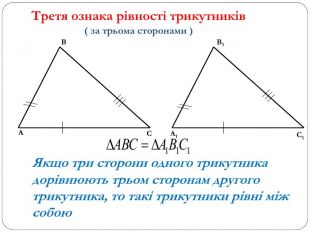
Трикутник. Опорні схеми до теми
Про матеріал
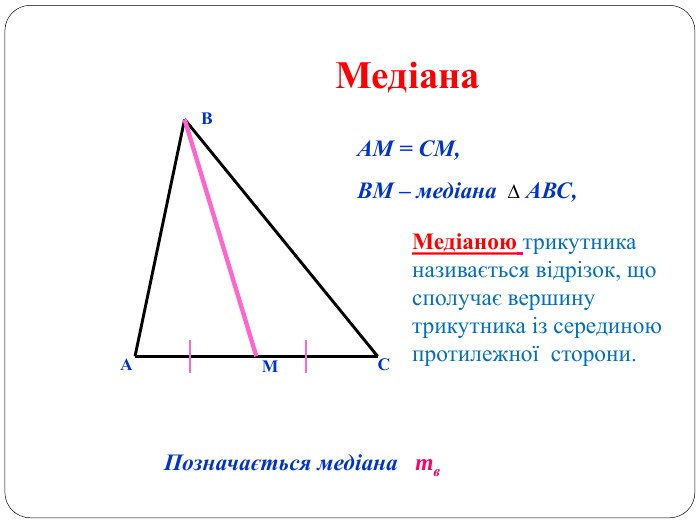
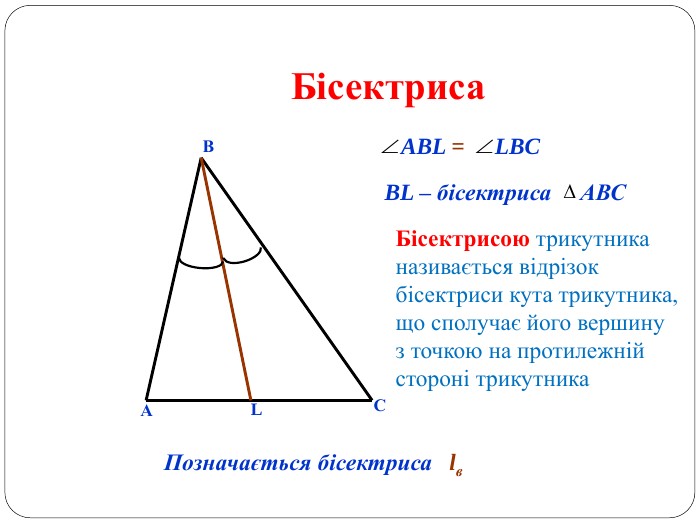
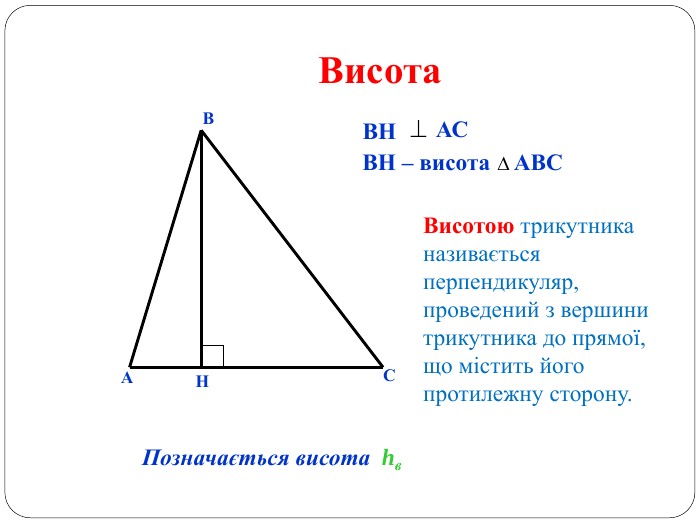
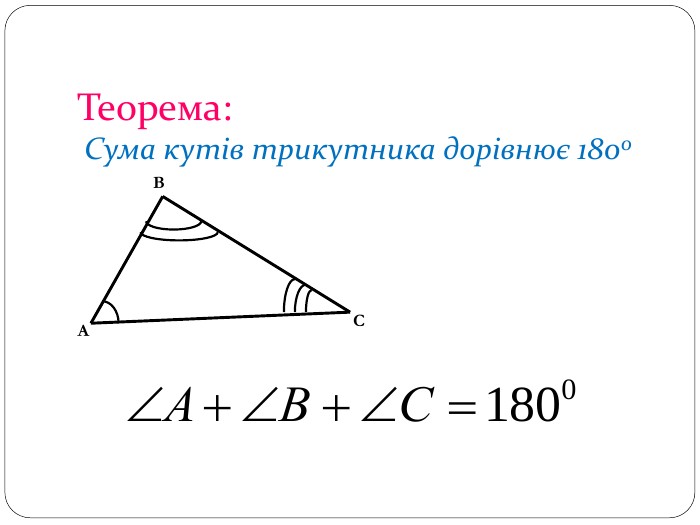
Матеріал може бути використаний при вивченні теми " Трикутник" та для повторення навчального матеріалу по даній темі. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку