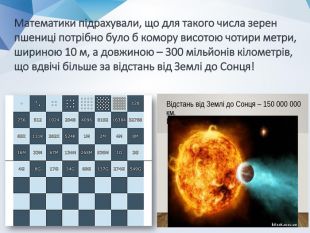
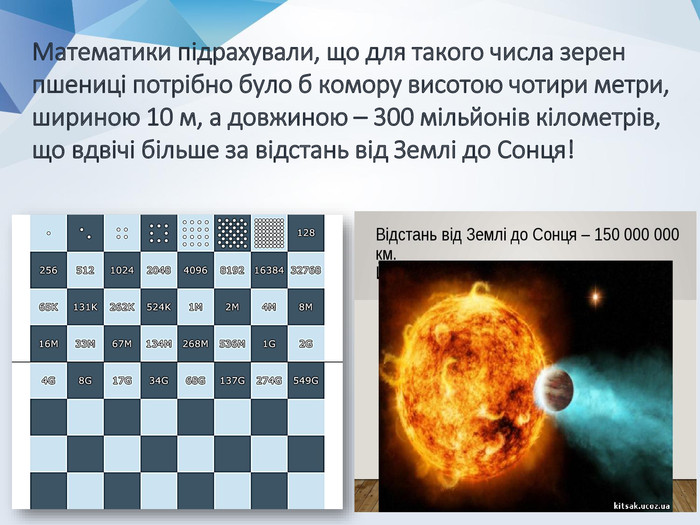
Презентація: "Симетрична стратегія"

Симетрична стратегія. Роботу виконав: Прохорчук Дмитро,учень 10 класу. КЗШ І-ІІІ ступенів № 123

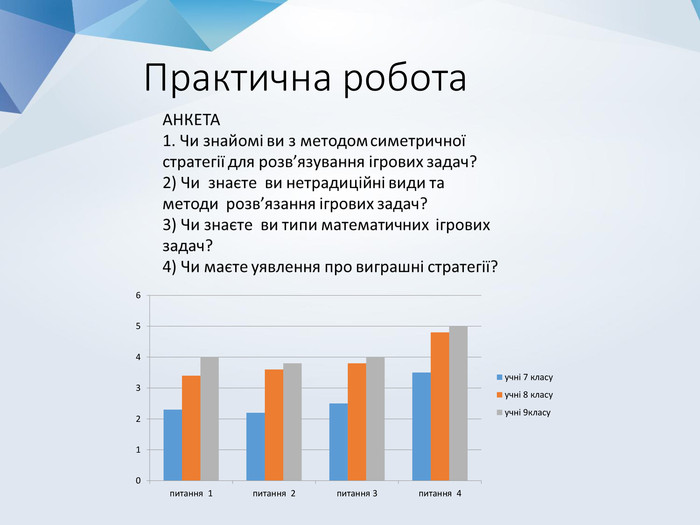
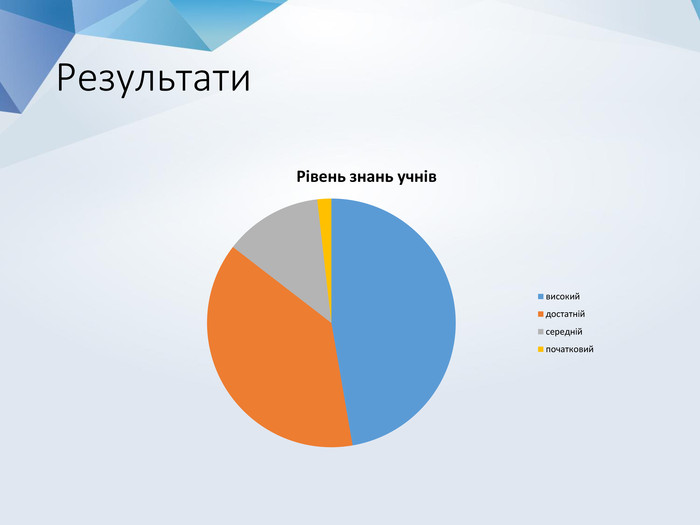
Мета роботи: глибоко проаналізувати задачі, здійснивши класифікацію у двох напрямках: за методами розв’язування та за наявністю стратегії у того чи іншого гравця; виробити алгоритм застосування методу при розв'язуванні ігрових задач. Гіпотеза: для будь-якої ігрової математичної задачі можна знайти виграшну стратегію. Проблемне питання: чи можно розглядати ігрові задачі як моделі деяких реальних ситуацій, конфліктів?Об'єкт дослідження: ігрові задачі, симетрична стратегія виграшу. Предмет дослідження: ігрові задачі на застосування методу симетрії.

З давніх – давен люди полюбляють грати в різні ігри. Однією з найулюбленіших були і залишаються шахи.

Перші шахи - «Чатуранга» ( «чотири частини»)

Легенда розповідає, що гра в шахи так сподобалася індійському правителеві – раджі, що він запропонував винахіднику будь-яку винагороду. Здивувався раджа, коли той зажадав не золота чи срібла, а звичайних пшеничних зерен.

Математики підрахували, що для такого числа зерен пшениці потрібно було б комору висотою чотири метри, шириною 10 м, а довжиною – 300 мільйонів кілометрів, що вдвічі більше за відстань від Землі до Сонця!

Шахи – улюблена гра багатьох поколінь

Катерина Велика. Наполеон IІван ГрознийІсаак Ньютон. Михайло Кутузов. Михайло Ломоносов. Видатні любителі шахів

Теорія ігор - математичний метод вивчення оптимальних стратегій в іграх. Під грою розуміється процес, в якому беруть участь дві і більше сторін, що ведуть боротьбу за реалізацію своїх інтересів. Кожна із сторін має свою мету і використовує деяку стратегію, яка може вести до виграшу або програшу, - залежно від поведінки інших гравців.

Розглядаючи різні економічні моделі, дослідники прийшли до висновку, що найбільше діяльність учасника у межах економічної моделі схожа на гру проти інших гравців. Так їм в голову прийшла ідея прийняти економічну модель – як приватний випадок гри, а її учасників, які змагаються між собою – як гравців.

Джон Неш запропонував ідею рівноваги Неша – таку точку в грі (набір стратегій), в якій жоден гравець не може покращити свій виграш, одноосібно змінивши свою стратегію.

Наприкінці 40-х фон Нейман створив дві теорії. Одна з них перетворилася на computer science – сучасні комп’ютери побудовані на фон нейманівській архітектурі. Цікаво, що зараз, 70 років потому, computer science та теорія ігор зустрілися. Сучасна теорія ігор застосовується для дослідження інтернету, нові протоколи тестуються за допомогою теорії ігор.

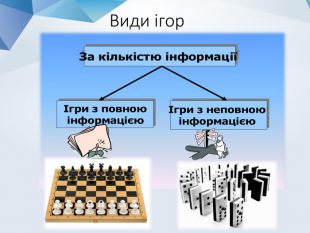
Ігрові задачі Ігрові задачі є типовим класом задач, які традиційно відносяться до інтелектуальних. Методи програмування ігрових задач найтіснішим чином пов'язані з методами планування цілеспрямованих дій і прийняття рішень.гравці – сторони, що беруть участь у конфліктівиграш – результат конфлікту.

Види ігор

Виграшні стратегії Стратегія — це вичерпно повний план дій того чи іншого гравця. Результати ігор бувають трьох типів: виграш першого гравця, виграш другого гравця нічия Стратегія успіху (або виграшна стратегія) - в теорії ігор план гри, реалізація якого дозволяє гравцю одержати перемогу незалежно від дій суперника.

Види стратегій

Вибір виграшної стратегіїДля знаходження стратегії перемоги можна використовувати такі ідеї:

Гра «Нім»Нім — математична гра, в якій два гравці по черзі беруть предмети, розкладені на кілька купок. За один хід може бути взято будь-яку кількість предметів (більше нуля) з однієї купки. В нормальній грі виграє гравець, який взяв останній предмет, в мізер-грі такий гравець програє.

Гра «Баше»Окремий випадок гри Нім, коли купка одна, але максимальне число предметів, які можна взяти за хід, обмежена, відома як гра Баше. Гра Баше́ — математична гра, в якій двоє ігроків из купки, яка спочатку має N предметів, по черзі беруть не менш ніж один предмет та не більше М предметів. Програє той, кому більше немає чого брати.

L-гра L-гра — проста настільна стратегічна гра, яку винайшов Едвард де Боно. Вперше він її описав у своїй книзі «The Five-Day Course in Thinking» (П'ятиденний курс мислення) у 1967 році.

Симетрія в математиціосьова симетрія (симетрія відносно прямої), центральна симетрія (симетрія відносно точки) дзеркальна симетрія (симетрія відносно площини).

Природа - дивовижний творець і майстер.

Симетрична стратегія. Симетрична стратегія -потужний і красивий методом рішення ігрових задач. Суть його - робити кожного разу хід, симетричний ходу противника або доповнити його до чогось.

Ігрові задачі1. У таблицi розміром 1×13 клiтинок хлопчик i дiвчинка по черзі замальовують одну або двi сусiднi клiтинки. Перемагає той, хто замалює останню клiтинку. Хто виграє – хлопчик, який починає гру, чи дiвчинка?       O      

Ігрові задачі Оксанка й Оленка обривають на ромашцi пелюстки. За один раз можна зiрвати будь-яку одну пелюстку або двi, якi розташованi поруч. Виграє та дiвчинка, яка зiрве останню пелюстку. Гру починає Оксанка. Хто виграє, якщо на ромашцi: а) 24 пелюстки? б) 25 пелюсток?

Є дві купки камінців - по 7 у кожній. За хід можна взяти будь-яку кількість камінців, але тільки з однієї купки. Програє той, хто не може зробити хід. Хто виграє?

Двоє по черзі кладуть п'ятаки на круглий стіл так, щоб вони не накладалися один на одного і не виступали за край столу. Програє той, хто не може зробити хід. Хто виграє?

Симетрія в шахах. Двоє гравців по черзі ставлять на клітинки шахівниці розміром 25×25 фішки – один білого, а другий чорного кольорів. Кожна нова фішка ставиться на вільну клітинку. Забороняється лише ставити фішку на таку клітинку, для якої на всіх сусідніх із нею уже стоять фішки цього кольору (сусідніми вважаються ті клітинки, які мають спільну сторону). Програє той, хто не зможе зробити свій черговий хід. Хто виграє за правильної гри – той, хто починає гру чи його суперник?

Практичне використання теорії ігор. Використовують військові, які побачили в ній апарат для дослідження стратегічних рішень. В результаті застосування теорії ігор визначається не тільки діагноз пацієнта, а й дана можливість лікарю зважити ймовірності можливих діагностичних помилок.

Практичне використання теорії ігор. У соціальних науках апарат теорії ігор застосовується у психології для аналізу торгових угод та переговорів, а також для вивчення принципів формування коаліцій тощо. Стратегічна матрична гра може бути зведена до пари двоїстих задач лінійного програмування.

Практична робота

Cамостійна робота. Задача 1. Двоє дітей прикрашають ялинку. Новорічні кульки лежать у двох ящиках. За один хід кожен гравець може брати з будь-якого (тільки одно-го) ящика довільну кількість куль. Виграє той, хто бере останнім. Як має грати той гравець, що починає, щоб виграти, якщо в першому ящику 15 кульок, а в другому - 19 кульок?

Задача 2 Хлопчик та дівчинка по черзі зафарбовують клітинки прямокутної таблиці. За один хід треба зафарбувати дві не зафарбовані клітинки, які мають спільну сторону. Починає гру дівчинка, а програє той, хто немає можливості зробити хід. Хто переможе при правильній грі, якщо таблиця має розміри 10*8? Cамостійна робота

Результати

Власні задачі Задача 1 Нехай дано будь-який n-кутник. За один хід гравець може провести одну діагональ таку, щоб кількість кутів у більшої утворенної фігури(зафарбована частина на малюнку) відрізнялася від кількості кутів початкової фігури не більш, ніж на 3. Програє той, хто не зможе провести діагональ. Хто з гравців може забезпечити собі виграш?

Задача 2 Дві конкуруючі фірми набирають співробітників. Перед ними лежить стос анкет працівників. Останньою лежить анкета найкращого спеціаліста, якого жадала б одержати кожна з фірм. Представники фірм одержують анкети на розгляд почергово, беручи від 1 до 4 аркушів за один раз. Якою повинна бути стратегія у представника, щоб одержати анкету найкращого робітника? Власні задачі

Якою повинна бути стратегія у представника, щоб одержати анкету найкращого робітника?

Задача 4 Дві будівельні компанії отримали завдання побудувати будівельні майданчики у місті. Кожний район представлений шестикутником. Будують компанії по черзі. За один тиждень (хід) можна побудувати або 1, або 2 дитячі майданчики у сусідніх районах. Компанія, яка побудує останньою, не отримає премії. Якої стратегії треба притримуватись компаніям, щоб отримати винагороду? Власні задачі

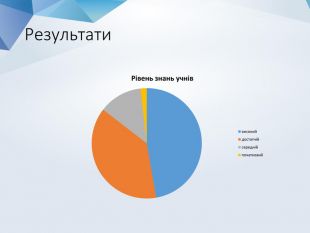
Висновок Розв’язання ігрових математичних задач сприяє розвитку математичних здібностей людини, допомагає вирішувати найскладніші математичні завдання, розвиває логіку, увагу, сприяють надбанню уміння самостійно приймати рішення,передбачати результат та шукати вихід із певної ситуації, проявляючи творчість,що використовується не лише в різних науках, а й у повсякденному житті.