Удосконалення методики проведення уроків розв’язування задач на рівномірний та нерівномірний прямолінійний рух

 

ЗЗСО «Корецький ліцей»

 

 

 

 

 

 

 

 

 

 

 

Удосконалення методики

проведення уроків розв’язування задач на рівномірний та нерівномірний прямолінійний рух

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2022

 У брошурі розглянуто  типові задачі на знаходження середньої швидкості, рух тіл за течією та проти течії річки.

 Підготував вчитель фізики Сімчук В. Є.

 

 

2022 р.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

 

1. Нерівномірний рух. Середня швидкість ................ 4

 

2. Рух за течією та проти течії річки ............................. 9

 

3. Використана література ………………………………… 19

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Нерівномірний рух. Середня швидкість

 

Під час вивчення поняття середньої швидкості та розв’язування задач у 7 класі та й у старших класах в учнів виникає досить багато труднощів. Тому, на мою думку, узагальнення та систематизація знань з цієї теми є досить важливим.

 Тут ми розглянемо найбільш типові задачі та помилки, які досить часто виникають під час їх розв’язування.

 Задача 1. Першу половину часу автомобіль рухався з швидкістю 50 км/год, а другу половину часу – з швидкістю 70 км/год. З якою середньою швидкістю рухався автомобіль?

Оскільки t₁ = t₂, то

ʋ_c = S/t = (S₁ + S₂)/ t₁ + t₂ = (ʋ₁t₁ + ʋ₂t₂)/(t₁ + t₂) = (ʋ₁t_{1 +} ʋ₂t₁)/ 2t₁= (ʋ₁ + ʋ₂)/2.

ʋ_c =(ʋ₁ + ʋ₂)/2.

ʋ_c = (50 + 70)/2 = 60 км/год.

 Дану задачу можна узагальнити для будь-якої кількості n рівних інтервалів часу. Тоді

 

ʋ_с = (ʋ₁ + ʋ₂ + ... + ʋ_n)/n.

 

Тобто, середня швидкість є середнім арифметичним швидкостей на кожному з інтервалів часу.

 Задача 2. Першу половину шляху автомобіль рухався з швидкістю 50 км/год, а другу половину шляху – з швидкістю 70 км/год. З якою середньою швидкістю рухався автомобіль?

Оскільки S₁ = S₂, то ʋ_с =  S/t = (S₁ +S₂)/(t₁+ t₂) =

= 2S₁/ (S₁/ʋ₁ + S₁/ʋ₂) =2ʋ₁ʋ₂/(ʋ₁ + ʋ₂)

 Тоді  ʋ_с =  2∙50∙70/(50 +70) = 58,(3) км/год.

 Для трьох рівних відрізків шляху формула буде мати вигляд такий:

                                ʋ_с    =    .

    

 Можна узагальнити дану формулу для n рівних ділянок шляху (середня швидкість є середнім гармонійним швидкостей на рівних відрізках шляху):

 

                      ʋ_с  =   .

 

Якщо учні засвоять алгоритм розв’язування таких задач, тоді труднощів при розв’язуванні задач на середню швидкість виникати не буде. Адже практично всі задачі, які пов’язані з середньою  швидкістю можна звести до двох випадків, які розглянуті вище.

Задача 3. Третину часу автомобіль рухався зі швидкістю 15 м/с, а решту часу – зі швидкістю 30 м/с. Обчисліть середню швидкість автомобіля.

 З умови задачі зрозуміло, що мова йде про три рівні інтервали часу. Тому скористаємося висновками задачі 1. ʋ_с = (ʋ₁ + ʋ₂ + ʋ₃) /3.

ʋ_с = (15 + 30 + 30)/3 = 25 км/год.

Задача 4.  Третину шляху автобус рухався зі швидкістю 40 км/год, решту шляху – зі швидкістю 60 км/год. Знайдіть середню швидкість за весь час руху.

 У цій задачі, як видно з умови, йдеться про три рівні відрізки шляху. Тому для її  розв’язання скористаємося висновками задачі 2. Для спрощення обчислень формулу запишемо так:

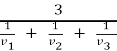                              =     , тоді

 

=   ≈ 51,7 км/год.

Задача 5. Автомобіль  проїхав половину шляху зі швидкістю 90 км/год. Другу половину шляху автомобіль рухався зі швидкостями 20 км/год та

40 км/год упродовж рівних проміжків часу. Знайдіть середню швидкість (у км/год) за весь час руху.

 Аналізуючи задачу, бачимо, що другу половину шляху               автомобіль долав впродовж рівних проміжків часу зі швидкостями 20 та 40 км/год. Тому тут середню швидкість обчислюємо як середнє арифметичне швидкостей: ʋ_с= (ʋ₂ + ʋ₃)/2;  ʋ_с = (20 + 40)/2 = 30 км/год

 Щоб обчислити середню швидкість за весь час руху, скористаємося формулою середньої швидкості для двох рівних відрізків шляху:

                          =     ;  = 45 км/год

Або, узагальнивши обидві формули, будемо мати такий вираз:

                          =     = 45 км/год

 Інші типи задач – це задачі, у яких відома середня швидкість на всій ділянці, а обчислити необхідно швидкості на її окремих частинах.

Задача 6. Першу половину часу автомобіль рухався зі швидкістю удвічі більшою, ніж швидкість на другій ділянці. Середня швидкість автомобіля на всій ділянці дорівнює 30 км/год. Визначте швидкість автомобіля на кожній з ділянок.

 Для двох рівних проміжків часу формула для обчислення середньої швидкості матиме вигляд:

ʋ_c =  (ʋ₁ + ʋ₂)/2.

Виходячи з умови задачі    ʋ₁=2ʋ₂, тоді ʋ_c =  3ʋ₂/2. Звідси   ʋ₂= 2ʋ_c/3, Тоді ʋ₂ = 20 км/год, а ʋ₁= 40 км/год.

Задача 7. Першу половину шляху автомобіль рухався зі швидкістю удвічі меншою, ніж швидкість на другій половині. Середня швидкість автомобіля на всій ділянці дорівнює 40 км/год. Обчисліть швидкість автомобіля на кожній ділянці шляху.

 Для двох рівних ділянок шляху формула для обчислення середньої швидкості матиме вигляд:

                              ʋ_с  =    .

 

Оскільки за умовою задачі ʋ₂  = 2ʋ₁, то                                            

                                             ʋ_с   =    .

Скоротивши дріб, матимемо ʋ_с = 4/3 ʋ₁. Тоді ʋ₁=3/4ʋ_с = = 30 км/год, а  ʋ₂  = 60 км/год.             

 

Рух за течією та проти течії річки

 

Особливе місце серед задач як з фізики так і з математики займають задачі на рух за і проти течії річки.

 Задача 8. Відстань між двома пристанями за течією катер проходить за 8 годин, а проти течії за 12 годин. За який час катер пройде цю відстань у стоячій воді? За який час цю відстань пройде пліт?

 Типовою помилкою при розв’язуванні таких задач є знаходження часу як середнього арифметичного, тобто (8 + 12) : 2 = 10 годин.

 Нижче буде запропоновано два способи розв’язання цієї задачі.

Спосіб 1. Так як пройдений шлях тут є сталим числом, то 8(ʋ_cт + ʋ_т) = ʋ_ст t_ст = 12(ʋ_ст – ʋ_т) , прирівнюючи ліву і праву частину цієї рівності будемо мати  ʋ_т = 0,2 ʋ_cт. Підставивши замість швидкості течії вираз для швидкості катера у стоячій воді будемо мати

8(ʋ_cт + 0,2 ʋ_cт) = ʋ_ст t_ст, тоді t_ст = 9,6 год.

 Узагальнюючи результат можна записати формулу, яка пов’язує швидкість течії з швидкістю катера у стоячій воді, якщо відомі проміжки часу руху за і проти течії:             

                          =      .

 Спосіб 2.   Цей спосіб ґрунтується на тому, що швидкість катера у стоячій воді є середнім арифметичним швидкостей за і проти течії річки, тобто ʋ_cт  =(ʋ_за + ʋ_проти)/ 2. Тоді, враховуючи, що ʋ= S/t, будемо мати:

S/t_ст =(S/t_за +S/t_проти)/2. Скоротивши S та перетворивши вираз, будемо мати формулу:

       

         t_ст  =   , тоді t _ст = 2· 8 · 12/20 = 9,6 год. 

                  

   Таким чином час руху катера в стоячій воді, за умовою даної задачі, не є середнім арифметичним проміжків часу руху за та проти течії, а середнім гармонійним.

 Можна скласти таблицю швидкостей та відстані між пристанями.             

S, км	ʋcт, км/год	ʋт,  км/год	tст, год	ʋс, км/год
72	5	1	9,6	4,8
96	10	2	9,6	9,6
144	15	3	9,6	13,(09)
192	20	4	9,6	19,2

 Як видно з таблиці швидкість катера у стоячій воді та середня швидкість катера, виходячи з умови задачі, не є рівними.

 Для обчислення часу, за який цю відстань здолає пліт, необхідно скористатися тим фактом, що швидкість течії можна обчислити за формулою:

ʋ_т  = (ʋ_за — ʋ_проти)/ 2.  Тоді, враховуючи, що ʋ = S/t, будемо мати S/t_т =(S/t_за — S/t_проти)/2. Скоротивши S та перетворивши вираз, будемо мати:

 

            t _т  =   , тоді t _т = 2· 8 · 12/4  = 48 год.

 

 Таким чином пліт здолає цю відстань за 48 годин.             

 Задача 9.  Швидкість руху човна відносно води у 2 рази більша, ніж швидкість течії. У скільки разів  човен довше пливе  між двома пристанями  проти течії, ніж за течією?

 Для розв’язування задачі використаємо формулу із задачі 8:                    

                          ʋ_т =     

Підставляючи ʋ_cт = 2 ʋ_т  та перетворивши вираз, будемо мати:  t_проти = 3t_за . Тобто у три рази довше.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Використана література

 

1. Велика книга ерудита, Київ. «Махаон-Україна», 2005.
2. В. Сиротюк, фізика 8, підручник для загальноосвітньої школи, 2005.
3. Фізика: Комплексна підготовка до зовнішнього незалежного оцінювання/ Уклад.: Н. Струж, В. Мацюк, С. Остап’юк. – Тернопіль: Підручники і посібники, 2013. – 464 с.