Урок - практикум з геометрії у 8-му класі по темі:"Вписані та описані чотирикутники. Практичне застосування їх властивостей."
Створення ландшафтного дизайну на основі властивостей вписаних і описаних многокутників навколо кола. Робота в групах з підручним матеріалом. Клас з допрофільним вивченням математики.

Розроблено та проведено вчителем математики
ЗОШ № 7 ім. В. В. Бражевського м. Житомира
Сергієм Олександровичем Сафонюком

Підвести учнів до самостійного визначення теми уроку. Для цього задати наступні питання:
1. Які фігури ми вивчаємо ?
2. Яке може бути їх взаємне розташування?
3. Де можна застосувати набуті знання, вміння та навички, набуті при вивченні теми?
Примітка: Кожне питання/відповідь супроводжується мультимедійною презентацію.
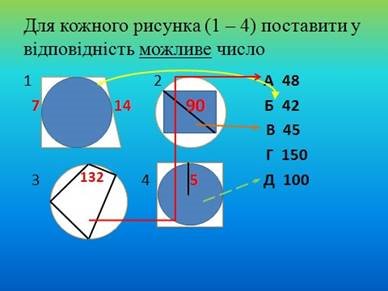
Для актуалізації опорних знань проводиться математичний диктант, який складається з двох частин.
Частина 1.


 Примітка: Кожна
відповідь
Примітка: Кожна
відповідь
супроводжується мультимедійною презентацію.
Перевірка відповідей проходить за принципом:
« Я твою, а ти мою».
Клас розбивається на 2 групи. Кожна група є претендентом на отримання роботи на фірмі, яка спеціалізується на розробці та створенні ландшафтного дизайну. Учитель оголошує завдання для груп, яке і буде метою уроку.

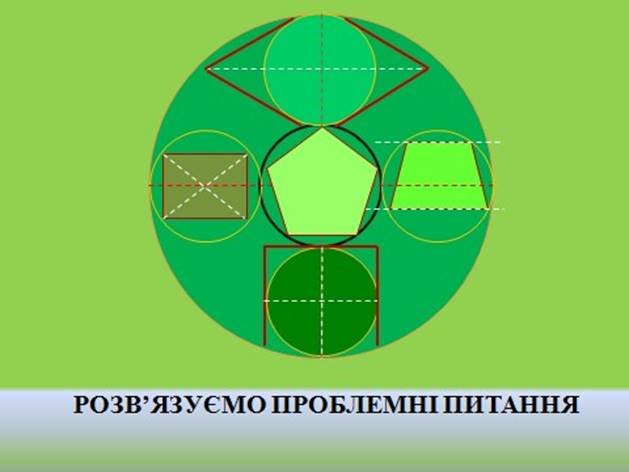
Вимоги до квітника: 1) він круглої форми; 2) всередині розташувати 5 клумб – 1 по центру і 4 на однаковій відстані від центра та одна від одної (клумби круглі); 3) в одній розташувати прямокутник; 4) навколо другої описати ромб; 5) третю вписати в квадрат; 6) в четверту вписати трапецію; 7) в центральній розташувати правильний п’ятикутник.
Групи користуються фігурою, що містить прямий кут, планкою без поділок та ниткою (мотузкою), вдягненою на олівець.
Ставляться проблемні питання.
Питання1. Як знайти центр кола?
 Крок 1: вписати 2 прямих
кути в коло 1. 2. Крок 2: через точки
перетину сторін кутів з колом провести 2 прямі. Контрольне
питання: яка властивість кутів застосована?
Крок 1: вписати 2 прямих
кути в коло 1. 2. Крок 2: через точки
перетину сторін кутів з колом провести 2 прямі. Контрольне
питання: яка властивість кутів застосована?
Відповідь: вписані прямі кути «спираються» на діаметри.
Супровід відповідей учнів та вирішення проблеми проводиться за допомогою мультимедійної презентації. Причому реальна побудова відбувається і на дошці, і в зошитах.
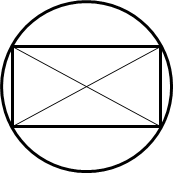
 Питання 2. Як
вписати прямокутник в коло? Очікувана відповідь: провести два діаметри, які
перетинаються не під прямим кутом. Нестандартні відповіді: провести дві,
паралельні до діаметра, хорди по різні сторони від нього і на однаковій
відстані від центра; провести дві, перпендикулярні до діаметра, хорди по різні
сторони від нього і на однаковій відстані від центра. Контрольне питання:
яка властивість прямокутника застосована? Відповідь: діагоналі
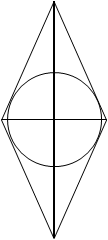
прямокутника є діаметрами описаного навколо нього кола. Питання 3. Як
описати ромб навколо кола? Як один із варіантів відповіді: продовжити взаємно
перпендикулярні діаметри. На одному з них відмітити на однаковій відстані від
центра дві точки. Через них провести до кола паралельні дотичні і знайти точки
їх перетину з продовженням іншого діаметра.
Питання 2. Як
вписати прямокутник в коло? Очікувана відповідь: провести два діаметри, які
перетинаються не під прямим кутом. Нестандартні відповіді: провести дві,
паралельні до діаметра, хорди по різні сторони від нього і на однаковій
відстані від центра; провести дві, перпендикулярні до діаметра, хорди по різні
сторони від нього і на однаковій відстані від центра. Контрольне питання:
яка властивість прямокутника застосована? Відповідь: діагоналі
прямокутника є діаметрами описаного навколо нього кола. Питання 3. Як
описати ромб навколо кола? Як один із варіантів відповіді: продовжити взаємно
перпендикулярні діаметри. На одному з них відмітити на однаковій відстані від
центра дві точки. Через них провести до кола паралельні дотичні і знайти точки
їх перетину з продовженням іншого діаметра.
Контрольне питання: яка властивість ромба застосована?
Відповідь: точка перетину діагоналей ромба є центром вписаного кола.
Питання 4. Як описати квадрат навколо кола?
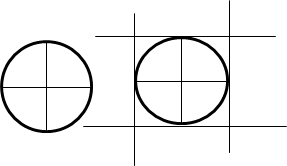 Як один із варіантів
відповіді. 1. 2.
Як один із варіантів
відповіді. 1. 2.
Крок 1: провести два взаємно перпендикулярних діаметра.
Крок 2: через кінці діаметрів провести перпендикулярно до них дотичні.
Контрольне питання: яка властивість квадрата застосована?
Відповідь: діаметр кола, вписаного в квадрат, дорівнює його стороні.
Питання 5. Як вписати трапецію в коло?
 Як один із варіантів
відповіді. Провести дві паралельні хорди до діаметра кола на різній відстані
від його центра. З’єднати кінці хорд. Контрольне питання: яка
властивість трапеції застосована?
Як один із варіантів
відповіді. Провести дві паралельні хорди до діаметра кола на різній відстані
від його центра. З’єднати кінці хорд. Контрольне питання: яка
властивість трапеції застосована?
Відповідь: в коло можна вписати рівнобічну трапецію, бо суми протилежних її кутів дорівнюють 1800.
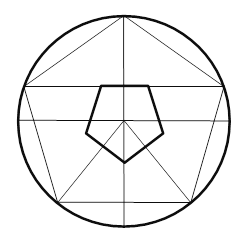
Залишилось одне питання – питання 6. Як з підручних засобів зробити правильний п'ятикутник і вписати його в коло?
Візьміть прямокутну стрічку паперу та зробіть вузол, який за формою дає правильний п'ятикутник.
Щоб вписати п'ятикутник в коло зробимо наступні кроки:
1) проведемо серединні перпендикуляри до його сторін (досить трьох) – це буде центр описаного (вписаного) кола;
2) сумістимо центр п'ятикутника з центром кола так, щоб одна його сторона була паралельна до діаметра кола;
3) продовжимо побудовані перпендикуляри до перетину з колом і проведемо пряму через сторону, яка паралельна до діаметра кола – отримаємо 5 точок; 4) з'єднаємо ці точки – отримали шуканий п'ятикутник.

Групи показують зроблені ескізи. Мультимедійна презентація результатів роботи.
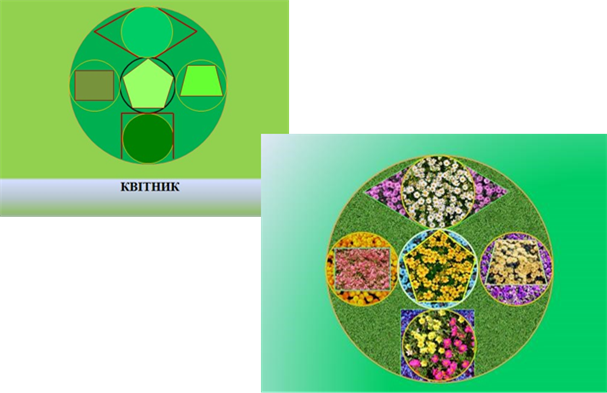
Проблемна задача

Розв'язування
а) проводимо діагоналі прямокутника, точка перетину яких і є центром описаного навколо нього кола та рівновіддалена від його вершин.
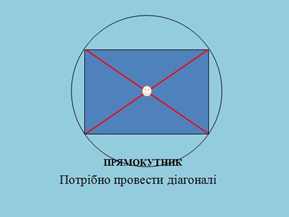
б) проводимо два серединних перпендикуляри до сторін трапеції, точка перетину яких і є центром описаного навколо неї кола та рівновіддалена від її вершин.

в) задача не завжди матиме розв'язок, як з прикладом ромба. Потрібно, щоб суми протилежних кутів чотирикутника дорівнювали 1800.

Домашнє завдання
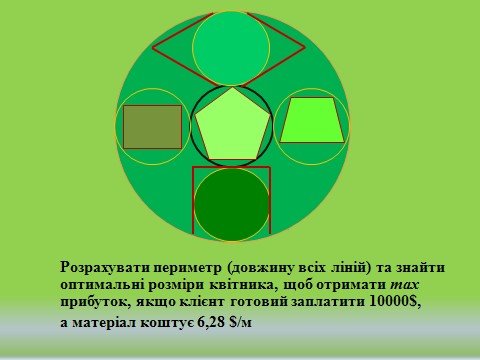
Поради учням: виміряти реальні розміри побудованих фігур, обчислити вартість отриманого квітника та скласти пропорцію.
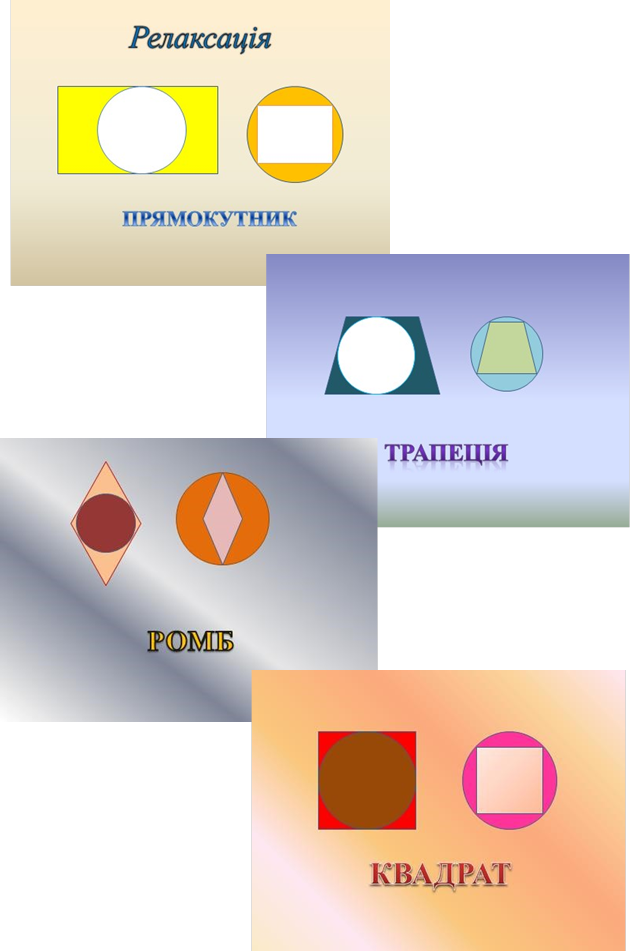
Під час підведення підсумків уроку проводиться "релаксація", коли в усній формі учні відповідають на питання: яка властивість виконується/не виконується на запропонованих слайдах.


про публікацію авторської розробки
Додати розробку
