З досвіду роботи "Розвиток процедурної математичної компетентності в учнів старшої школи"

Розвиток процедурної математичної  компетентності

 в учнів старшої школи.

 

      Щоб не зв’язувати ініціативи учня типовими задачами, треба, щоб цих основних груп було по можливості небагато. У зв’язку з цим в основу типізації задач слід покласти не зовнішній текст задачі, а її математичний зміст.

                                                  О.М.Астряб

    З метою формування в учнів самостійності, відповідальності, формування їхньої активної життєвої позиції перед педагогами постають особливі завдання, які визначаються потребою не лише повідомляти учням готові знання, але й навчити здобувати їх самостійно, спонукати учнів проявляти пізнавальний інтерес. На даному етапі розвитку педагогічної науки і сучасної школи особливе значення набула проблема оволодіння вчителем нових методичних прийомів роботи, за допомогою яких  можна значно активізувати розумову діяльність учнів і їх навчальну діяльність на уроці.

     Хочу поділитися своїм досвідом викладання геометрії у 11 класі.

     Особливого значення в курсі геометрії старшої школи набувають теми «Многогранники», «Тіла обертання», «Комбінації геометричних тіл». У процесі вивчення даних тем суттєво розвивається просторова уява учнів, а також здібності та вміння поводити операції над просторовими об’єктами.  Але окремим учням буває важко уявити геометричні тіла, розглядати співвідношення окремих їх елементів, їх взаємне розміщення. А ще важче віднайти найраціональніший спосіб розв’язання тих чи інших задач. У цьому випадку на допомогу учням можуть прийти опорні конспекти до розв’язування певних типів задач.

    Зупинимося на темі «Піраміда».

    Учням 11 класу  де інколи важко визначитися  у виборі способу розв’язання задач з даної теми. Особливо це можна помітити  при розв’язуванні учнями тих задач, де треба провести певне дослідження, довести той чи інший факт, що допоможе при наступному розв’язуванні задачі. Наприклад, довести, що дана точка О  є центром вписаного в основу чи описаного навколо основи кола, визначити, в яку  точку  буде проектуватися вершина піраміди тощо. В основному задачі «з пірамідами» можна поділити на декілька основних типів, до яких існують певні стандартні  підходи,  пояснивши які учням, можна  досягти  досить позитивних результатів при вивченні  даної теми. Саме це і спонукало мене створити такі «Шпаргалки» на допомогу учням, які вони можуть використовувати  під час процесу засвоєння ними способів розв’язування  задач з теми «Піраміда».

Задачі І типу.

Піраміди, в яких бічні ребра рівні або

 нахилені до площини основи під одним кутом

Малюнки до задач:

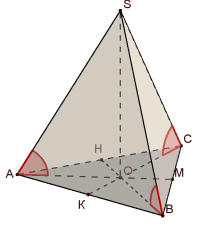
а) в основі – правильний трикутник:             б) в основі – квадрат, прямокутник:

 

 

 

 

в) в основі – прямокутний трикутник:        г) в основі – рівнобедрений трикутник:

Вказівки до розв’язання:

І. Нехай SO- висота піраміди. За умовою SAO=SBO=SCO… Тоді SAO=

=SBO=SCO… (за спільним катетом SO та гострим кутом). Звідси, АО=ВО=СО. Тому, точка О є центром описаного навколо трикутника (чотирикутника) кола .

R =АО=ВО=СО.

  (далі йде  розв’язування задачі  за тими даними, що є в умові для  обчислення площі поверхні, об’єму піраміди тощо).

 

ІІ. Нехай SO- висота піраміди. За умовою SA=SB=SC=… Тоді SAO =

=SBO =SCO… (за спільним катетом SO та гіпотенузою). Звідси, АО=ВО=СО. Тому, точка О є центром описаного навколо трикутника (чотирикутника) кола .

R =АО=ВО=СО. Далі розв'язуємо за умовою…

 

Задачі ІІ типу.

Піраміди, в яких двогранні кути при основі рівні або бічні грані нахилені до площини основи під одним кутом

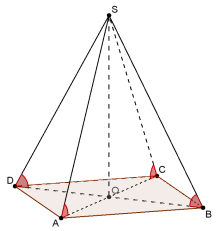
Малюнки до задач:

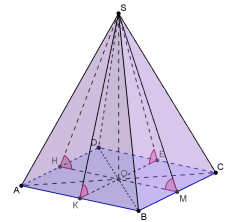а) в основі – правильний трикутник:             б) в основі – квадрат:

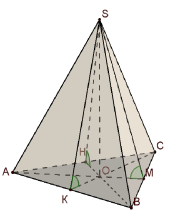
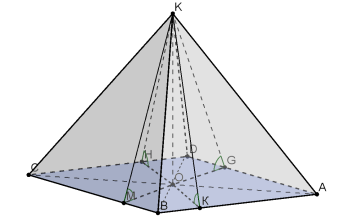
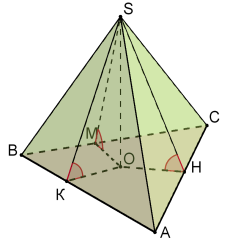в) в основі – довільний трикутник:                    г) в основі – ромб:

 

 

 

Вказівки до розв’язання:

     Нехай SO- висота піраміди. Проведемо ОКАВ, ОМВС, … Тоді за теоремою про три перпендикуляри (ТТП)  SКАВ, SМВС, …Звідси SKO=SMO=… - лінійні кути двогранних кутів при основі піраміди. За умовою SKO=SMO=… Тоді SKO=SMO=… (за спільним катетом SO та гострим кутом). Звідси, KО=MО=HО... Тому, точка О є центром вписаного у трикутник (чотирикутник) кола ;  r =KО=MО=HО.  Далі за умовою…

 

Задачі ІІІ типу.

Піраміди, в яких дві бічні грані або

 бічне ребро перпендикулярні до основи

 

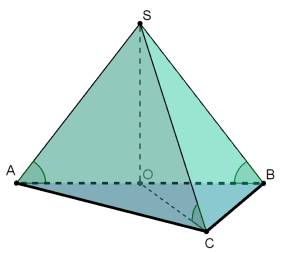
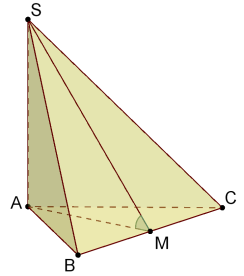
Малюнки до задач:

а) в основі – трикутник:                                б) в основі - квадрат, прямокутник:

 

 

 

 

 

 

 

 

 

 

 

 

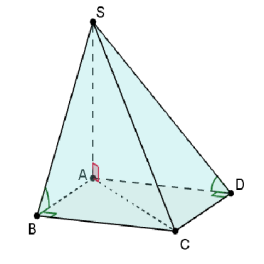
АМВС, SA(ABC),то за ТТП                       Аналогічно,  SВА  та SDА є                         SMBC. Тому SМА є кутом нахилу              кутами нахилу бічних граней (SBC)

 бічної грані (SBC) до площини основи.             та (SDC) до площини основи.

 

 

 

в)  в основі - ромб, в якому  суміжні                   г)  в основі - ромб, в якому  суміжні

перпендикулярні грані утворюють                 перпендикулярні грані утворюють

між собою гострий кут:                                        між собою тупий  кут:

 

 

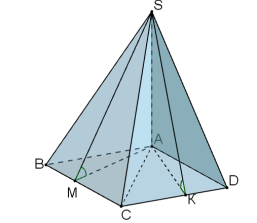
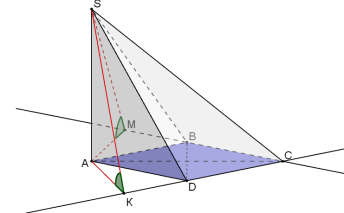
Початок розв'язання задачі з чотирикутною пірамідою, в основі якої - ромб:

   Оскільки (SAD) (ABC), (SAB) (ABC), то SA – висота піраміди. Проведемо АМВС, АКDC, тоді за ТТП SMBC, SKDC. За умовою SМА=SКА=… Тоді з рівності трикутників АSM  та  ASK випливає, що АМ = АК і т.д.

 

д) в основі – прямокутний трикутник:

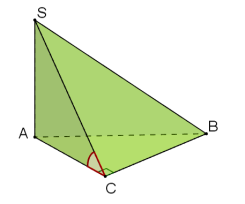
Оскільки, АСВС, SA(ABC), то за ТТП SCBC. Тому SСА є кутом нахилу бічної грані (SBC) до площини основи.

 

 

 

 

 

Задачі ІV типу.

Піраміди, в яких одна бічна грань перпендикулярна до основи

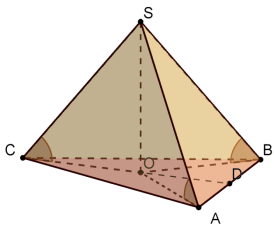
Малюнки до задач:

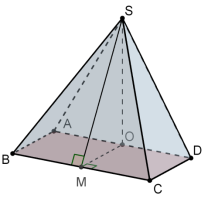а) в основі – трикутник:                                б) в основі - квадрат, прямокутник:

Розв’язання (для довільного трикутника, в тому числі для прямокутного з гіпотенузою АС):

  Нехай SO – висота піраміди. Оскільки (SAC) (ABC),то точка О належить АС. Проведемо ОМАВ, ОКВС, тоді за ТТП  SMAB, SKBC, тобто SМО =          SКO=… . Звідси, SМO=SКO (за катетом SO та гострим кутом). Тоді, ОМ = ОК  , тобто ОВ – бісектриса        АВС. (АО + ОВ = АВ).

(За даними задачі знаходимо ОМ і т.д.)

 

в) в основі – прямокутний трикутник з прямим кутом В:

 

Нехай SO – висота піраміди. Оскільки          (SВC) (ABC), то точка О належить ВС. За умовою     ВСАВ. Проведемо ОDАC, тоді за ТТП  SВAB, SDAC, тобто SBО  =            SDO=… . Звідси, SBO=SDO (за катетом SO та гострим кутом). Тоді, ОB = ОD  , тобто ОA – бісектриса АВС.

(За даними задачі знаходимо ОD і т.д.)

 

 

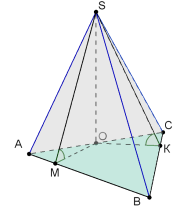
Задачі V типу.

Піраміди, в яких задано перпендикуляр,

 проведений з деякої точки до бічної грані

Малюнки до задач:

а) в основі – правильний трикутник:                 б) в основі - квадрат:

 

 

 

 

 

 

 

 

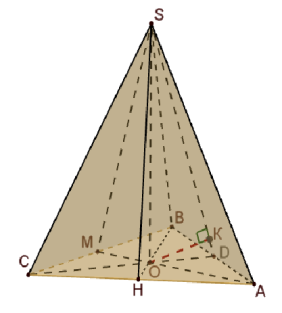
Початок  розв’язання задачі  (за малюнком (а) ):

  Нехай  SO – висота піраміди. Проведемо  ОК(SAB), SDAB. За ТТП  ОDAB. За  ознакою перпендикулярності прямої  і  площини  АВ(SOD). Оскільки, АВ (SAB), то (SAB) (SOD). Тоді OK(SOD), KSD. …

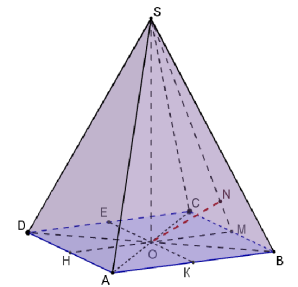
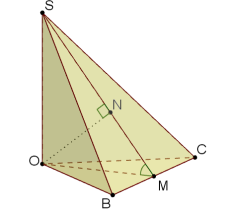в) трикутна піраміда, в якої дві бічні грані перпендикулярні до основи:

 

 

 

     Для  кращого розуміння даного матеріалу  учням пропоную  «відвідати»  свій  блог (http://gtg130364matem.blogspot.com), де вони можуть  розглянути 3-D  моделі до даних  типів задач.

 

     На початку вивчення стереометрії просторові знання учнів розвинені дуже слабо. Початкові відомості по стереометрії мають абстрактний характер, засвоєння матеріалу будується на заучуванні. Учні втрачають інтерес до предмету, і багато хто з них вважає стереометрію одним з найважчих предметів. Відображення просторових фігур у вигляді креслення на аркуші паперу призводить до того, що дуже багато закономірностей уявляються в спотвореному вигляді. Тільки вихід на іншу наочність може допомогти учням упоратися із завданнями, для вирішення яких потрібно бачити тіла «всередині», змінювати їх будову та розташування частин. І таким чудовим  інструментом для вчителя  став, зокрема,  програмний пакет  GeoGebra.

    «Комбінації геометричних тіл» - одна з найважчих тем  геометрії. Вона є розвитком системи всіх знань , умінь і навичок  курсів планіметрії та стереометрії, поглиблює і розширює курс геометрії і показує практичне застосування геометричних знань в реальному житті. При викладанні даної теми використовую також методику опорних конспектів та систему типових задач  на основі 3-D моделей комбінацій геометричних тіл. Даний матеріал викладено на сторінці «Задачі в середовищі GeoGebra» мого блогу.

Наприклад:

 І. Призма та циліндр

Теорія:

     Циліндром, вписаним в призму, називається циліндр, основи якого - круги, вписані в основи призми, а бічна поверхня циліндра дотикається бічних граней призми. 

Висота циліндра дорівнює висоті призми.

     Циліндр називається описаним навколо призми, якщо його основи - круги, описані навколо основ призми, а твірні збігаються з ребрами призми.

Висота циліндра дорівнює висоті призми.

Задача 1

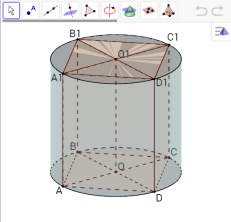   Діагональ осьового перерізу циліндра дорівнює 8 см і утворює з площиною його основи кут 30⁰. Знайдіть об’єм правильної чотирикутної призми, вписаної у циліндр.

 

 

 

 

 

 

 

 

Примітка: Розглядаючи, наприклад, дану задачу учні можуть «розвернути» ці геометричні тіла так, щоб зручно було споглядати осьовий переріз, потім провести у ньому діагональ  і  застосувати співвідношення у прямокутному трикутнику.

 

 

 

 

 

 

 

 

 

 

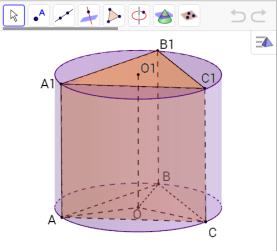Задача 2

   В основі прямої призми  лежить  трикутник з кутами α і β і радіусом описаного кола R. Діагональ бічної грані, що містить  сторону трикутника, для якої дані кути є прилеглі, нахилена до площини основи під кутом φ.  Знайти площу бічної поверхні циліндра, описаного навколо даної призми.

 

 

 

 

 

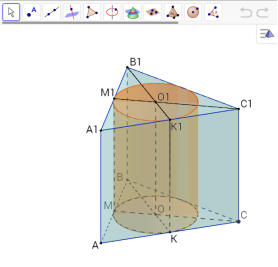
Задача 3

   Діагональ бічної грані правильної трикутної призми дорівнює d і нахилена під кутом φ до площини основи. Знайдіть об’єм циліндра, вписаного в цю призму.

 

 

 

 

 

 

 

 

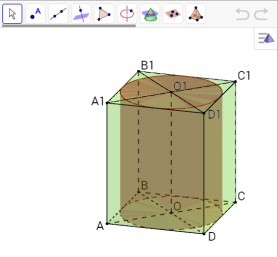
Задача 4

   Діагональ правильної чотирикутної призми дорівнює d і нахилена під кутом φ до площини основи. Знайдіть об’єм циліндра, вписаного в цю призму.

 

 

Додаткові  задачі:

1.  Основа прямої призми – прямокутний трикутник з катетом a і протилежним кутом α. Діагональ бічної грані, що містить гіпотенузу, нахилена до площини основи під кутом β. Знайти площу бічної поверхні циліндра, описаного навколо даної призми.

2. В основі прямої призми лежить прямокутник, площа якого S і кут між діагоналями α. Діагональ призми утворює з площиною осн6ови кут β. Визначити бічну поверхню циліндра, описаного навколо цієї призми.

3.  В основі прямої призми лежить прямокутний трикутник з гіпотенузою с і гострим кутом β. Діагональ грані, що містить протилежний до даного кута катет, нахилена до площини основи під кутом α. Визначити бічну поверхню циліндра, вписаного в дану призму.

4.  В основі прямої призми лежить ромб, площа якого S і тупий кут β. Діагональ бічної грані призми утворює з площиною основи кут α. Визначити бічну поверхню циліндра, вписаного в дану призму.

 

ІІ. Піраміда та конус

Теорія:

     Конусом, вписаним в піраміду, називається конус, основа якого - круг, вписаний у многокутник основи піраміди, вершина співпадає з вершиною піраміди, бічна поверхня конуса дотикається бічних граней піраміди.

 

    Конус називається описаним навколо піраміди, якщо його основа - круг, описаний навколо піраміди, вершина співпадає з вершиною піраміди, а твірні збігаються з ребрами піраміди.

     Висоти конуса і піраміди збігаються.

    Радіус вписаного в основу піраміди кола (круга) перпендикулярний стороні многокутника, який лежить в основі піраміди, і є проекцією твірної конуса на площину основи.

 

 

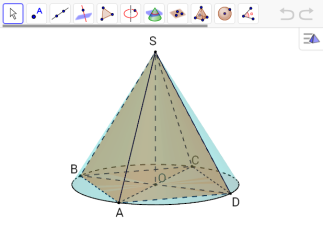Задача 1

   У  правильній чотирикутній піраміді апофема дорівнює l , а плоский кут при вершині – α. Знайти об’єм конуса, описанного навколо піраміди.

 

 

 

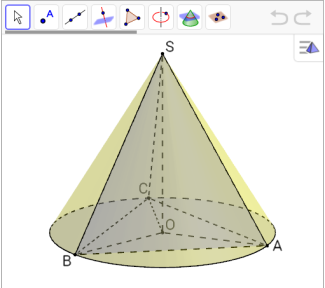
Задача 2

   Основа піраміди – рівнобедрений трикутник з кутом α при вершині. Всі бічні ребра піраміди рівні. Бічна грань піраміди, яка містить основу рівнобедреного трикутника, утворює з площиною основи кут φ. Знайдіть бічну поверхню конуса, описаного навколо піраміди, висота якої дорівнює Н.

 

Задача 3

   У правильній чотирикутній піраміді відстань від середини висоти піраміди до бічної грані дорівнює d. Знайдіть повну поверхню вписаного в піраміду конуса, твірна якого нахилена до площини основи під кутом α.

 

Задача 4

   У правильній трикутній піраміді апофема дорівнює m, а плоский кут при вершині – β.  Знайдіть об’єм конуса, вписаного в піраміду.

 

 

 

 

 

 

 

ІІI. Куля та піраміда

Теорія:

  Куля називається описаною навколо піраміди, якщо всі вершини піраміди лежать на поверхні кулі.

  Якщо вершина піраміди проектується в центр кола, описаного  навколо основи, то центр описаної кулі лежить на прямій, яка містить висоту піраміди в точці перетину цієї прямої з серединним перпендикуляром до бічного ребра.

   Куля називається вписаною в піраміду, якщо всі  грані піраміди дотикаються до кулі.

   Якщо вершина піраміди проектується в центр кола, вписаного в основу, то центр вписаної кулі лежить на висоті піраміди, в точці перетину висоти з бісектрисою лінійного кута двогранного кута  при основі піраміди.

 

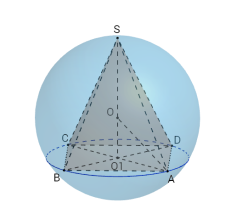Задача 1
 У правильній чотирикутній піраміді бічне ребро нахилене до основи під кутом α. Обчисліть об’єм піраміди, якщо радіус кулі, описаної навколо неї, дорівнює R.

 

 

 

 

 

 

 

 

 

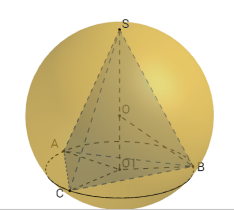Задача 2

 Плоский кут при вершині правильної  трикутної піраміди дорівнює α. Радіус кола, описаного навколо бічної грані, дорівнює R. Знайти об’єм описаної кулі.

 

 

 

 

 

 

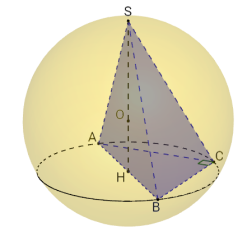
Задача 3

 В основі піраміди лежить прямокутний трикутник з гострим кутом α. Всі бічні ребра піраміди  нахилені до площини основи під кутом β. Знайдіть об’єм піраміди , якщо радіус кулі, описаної навколо неї, дорівнює R.

 

 

 

 

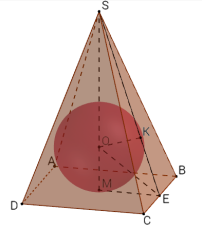
Задача 4

 У правильній чотирикутній піраміді двогранний кут при основі дорівнює α. Знайдіть площу повної поверхні піраміди, якщо радіус кулі, вписаної в неї, дорівнює r.

 

 

 

 

 

 

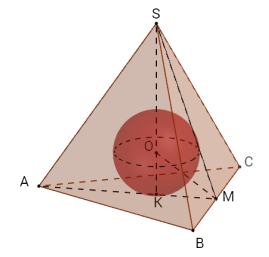
Задача 5

 У правильній трикутній піраміді двогранний кут при основі дорівнює β. Знайдіть об’єм  піраміди, якщо радіус кулі, вписаної в неї, дорівнює r.

 

 

 

 

 

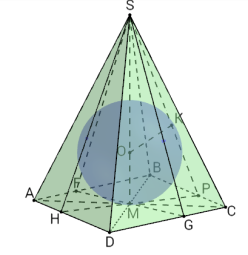
Задача 6

 В основі чотирикутної піраміди лежить ромб з тупим кутом β. Всі бічні грані нахилені до площини основи під кутом φ. Знайдіть об’єм піраміди, якщо відстань від центра вписаної кулі до вершини піраміди дорівнює d.

 

 

 

 

 

 

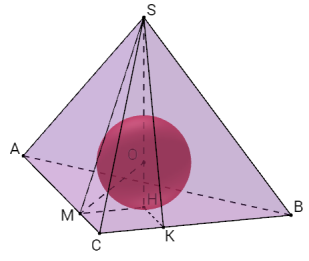Задача 7

 В основі піраміди лежить прямокутний трикутник з кутом β. Всі бічні грані нахилені до площини основи під кутом α. Знайдіть об’єм піраміди, якщо радіус кулі, вписаної в неї, дорівнює r.

 

 

 

    Таким самим чином систематизовано задачі та створено до них 3-D моделі з інших розділів теми: «Конус та куля»,  «Куля та призма», «Куля та циліндр».

 

 

    Аналогічні матеріали учні можуть знайти на сторінках мого блогу під час вивчення  тем  «Куля» та «Тіла обертання», де зібрано усі типові задачі даного напрямку. Навчившись їх розв’язувати на основі 3-D моделей, учень легко опанує дані теми та матиме належну підготовку до ЗНО.

    Наприклад, стикаючись із труднощами при розв’язуванні наступних задач з теми «Куля», учень може розглянути моделі до задач з «різних сторін» та легко знайти спосіб їх розв’язання.

1).  Діагоналі ромба – 15 см і 20 см. Куля дотикається до всіх його сторін. Радіус кулі – 10 см. Знайти відстань від площини ромба до центра кулі.

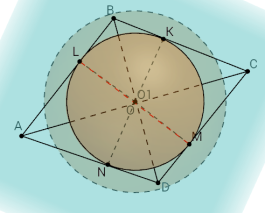
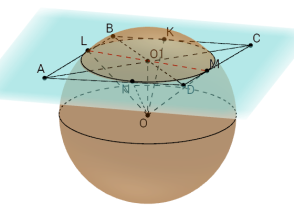
2). Трикутник, сторони якого дорівнюють 13 см, 14 см, 15 см дотикається до поверхні кулі. Знайти об'єм кулі, якщо відстань від центра кулі до площини трикутника дорівнює 5 см.

 

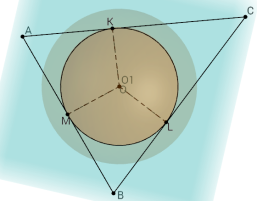
   Отже, використання системи типових задач на основі 3-D моделей та опорних конспектів при вивченні, зокрема, стереометрії значно покращує рівень засвоєння та розуміння учнями матеріалу. Таким чином, учні вчаться оперувати геометричними об’єктами на площині і в просторі, а зіткнувшись із подібними об’єктами у навколишній дійсності, зможуть ров’язати задачі практичного змісту.