Урок - захист творчих робіт "Арифметична та геометрична прогресії"
1
Л. Трохименко


Трохименко Любов Іллівна – учитель математики,
учитель вищої кваліфікаційної категорії
Автор пропонує методичну розробку уроку-захисту творчих робіт з теми: «Арифметична та геометрична прогресії.
У методичній розробці представлена індивідуальна форма роботи над рефератами та їх захист.
В даній роботі мова піде про прогресії, знаходження суми їх n перших членів; про найдавнішу прогресію; про розв’язування нестандартних задач, а також про одну важливу формулу для обчислення суми, а саме:
![]() , найрізноманітніших задач в різних питаннях математики.
, найрізноманітніших задач в різних питаннях математики.
Робота може бути корисною для вчителів математики середніх шкіл.
Передмова
У своїй роботі автор мав на меті задовольнити потребу дітей в творчості, дослідництві; розвивати здатність діяти, знаючи і розуміючи.
А також перевірити якість та міцність знань учнів за темою «Арифметична і геометрична прогресії», уміння застосовувати вивчене під час розв’язування вправ у стандартних та нестандартних ситуаціях.
Тема «Арифметична та геометрична прогресії» займає важливе місце у вивченні не тільки математики. Адже поняття «прогресія» та їх властивості, часто застосовують у фізиці, хімії та інших природничих науках.
Талант і творча обдарованість особистості стають сьогодні запорукою інтенсивного економічного розвитку країни і сприятливим чинником національного престижу. Розвитку в процесі навчання творчих здібностей учнів сприяють технології інтерактивного навчання.
Під час інтерактивного навчання учні вчаться бути демократичними, спілкуватися з іншими людьми, критично мислити, приймати продумані рішення.
На своїх уроках автор практикує інтерактивні технології «акваріум», «мікрофон», «незакінчені речення».
Вирішальне значення має формувальний вплив предмета математики на особистість школяра. Тому в цій роботі автор, насамперед, приділив увагу розвитку логічного мислення, інформаційної культури, уваги, пам’яті, позитивних властивостей особистості й рис характеру, емоційно-вольової сфери.
Універсальні генії (як от Ломоносов і Леонардо да Вінчі) народжуються раз на сто років. Хоч геніальні вони не в шкільному віці. Щоб у майбутньому стати успішним, необхідно подбати про сьогодення. Сприяючи ерудованості учнів з предмета ми допомагаємо їм опанувати загальні вміння навчати себе – вчитися.
Нерідко на шляху до зацікавлення розкривається талант дитини, про який вона й не підозрювала.
За два тижні до проведення уроку оголошується тема, дається список рекомендованої літератури, визначається термін написання рефератів та дата їх перевірки.
Тема: Арифметична та геометрична прогресії. Нестандартні задачі
Мета: узагальнити та систематизувати знання і вміння учнів з теми «Арифметична та геометрична прогресії»: формула n – го члена арифметичної та геометричної прогресій, суми їх n перших членів; формувати в учнів уміння застосовувати набуті знання в нестандартних умовах, аналізувати та систематизувати ті знання, які вони здобувають на уроках або з додаткової літератури; сприяти активізації розумової діяльності учнів, прищеплювати любов до математики; виховувати наполегливість у досягненні мети, дисциплінованість, вміння раціонально використовувати час
уроку.
Епіграф уроку:
Розв’язання простої, але не зовсім стандартної задачі може вимагати деякого напруження, зате натомість дає відчути тріумф відкриття.
Д. Пойа.
Тип уроку: узагальнення та систематизація знань і вмінь.
Форма проведення: урок – захист творчих робіт.
Обладнання: плакати з висловами математиків і про математику, роздавальний матеріал, таблиці з умовами задач, що розв’язуються усно, ілюстрації.
Девіз: «Швидкість потрібна, а поквапливість – шкідлива».
О. Суворов.
Хід уроку
І. Організаційний етап
Вступне слово вчителя. Добрий день, шановні друзі! Сьогодні в нас не зовсім звичайний урок. Незвичайний не тільки тому, що на ньому присутні гості, а й тому, що він пройде у вигляді захисту творчих робіт учнів. Урок нестандартний.
ІІ. Актуалізація опорних знань
Актуалізація опорних знань проводиться у вигляді усної роботи, під час якої вчитель звертає увагу на ключові означення та формули теми (деякі з них учні можуть записати в зошит).
План проведення усної роботи
|
№ |
Питання теоретичного матеріалу
|
Вправа |
|
1 |
Означення арифметичної прогресії |
Яка з наведених послідовностей є арифметичною прогресією? А)2;-6;12;-24; Б)3;7;11;15; В)2;4;8;16; Г)2;4;2;4. |
|
2 |
Означення різниці арифметичної прогресії.
|
Знайдіть різницю арифметичної прогресії, якщо |
|
3 |
Формула n-го члена арифметичної прогресії.
|
Перший член арифметичної прогресії |
|
4 |
Формула суми n перших членi арифметичної прогресії.
S
|
1.Чому дорiвнює сума семи перших членів арифметичної прогресії (
2. |
Продовження таблиці «План проведення усної роботи»
|
5 |
Означення геометричної прогресії |
Укажіть серед наведених послідовностей геометричну прогресію А)4;8;12;16; Б)10;20;30;40; В)5;6;8;11; Г)7;14;28;56 |
|
6 |
Означення знаменника геометричної прогресії |
Чому дорівнює знаменник геометричної прогресії ( |
|
7 |
Формула n-го члена геометричної прогресії
|
Чому дорівнює п'ятий член геометричної прогресії, якщо її перший член |
|
8 |
Формула суми n перших членiв геометричної прогресії.
|
Чому дорiвнює сума чотирьох перших членів геометричної прогресії, якщо її перших член |
ІІІ. Мотивація навчальної діяльності, повідомлення теми, мети, завдань уроку
Учитель. Урок-захист творчих робіт – це урок нетрадиційний, який розкриває ваші здібності, знання з теми «Арифметична і геометрична прогресії», розвиває фантазію.
Сьогодні ми перевіримо, як ви виконали домашнє завдання.
(Оголошуються прізвища доповідачів та порядок їх виступів).
Пам’ятайте девіз: «...Швидкість потрібна, а поквапливість шкідлива».
О. Суворов.
Як кажуть, попит породжує пропозицію. Якщо є задачі, то потрібно навчитися їх розв’язувати.
Розв’язування задачі ускладнюється тоді, коли у людини не досить розвинуто вміння побачити єдину математичну модель у різних ситуаціях. Не даремно Анрі Пуанкаре, французький математик, сказав: «Математика є спосіб називати різні речі одним ім’ям.»
Можливість розвивати це вміння ви матимете сьогодні, розв’язуючи задачі, пов’язані з прогресіями.
І, крім того, матимете гарну можливість розвинути і закріпити навички розв’язування вправ на обчислення сум.
ІV. Творче застосування узагальнених знань, навичок та вмінь
Не випадково відомий сучасний математик Д. Пойа говорить: «Що означає опанувати математику? Це є вміння розв’язувати задачі, до того ж не тільки стандартні, але й ті, що потребують відомої незалежності мислення, здорового глузду, оригінальності, винахідливості.»
Доповідачі виступають зі своїми повідомленнями, у кінці кожного виступу учні ставлять їм запитання.
Задача очень непростая:
Как сделать, чтобы быстро
От единицы и до ста
Сложить в уме все числа?
Пять первых связок изучи –
Найдешь к решению ключи!
Давным-давно один мудрец сказал,
Что прежде надо
Связать начало и конец
У численного ряда.
Існує традиційна розповідь про маленького Гаусса, який потім став великим Карлом – Фрідріхом Гауссом («король математиків» – лат.) – напівофіційне прізвище, яке було присвоєне Гауссу ще за життя. Ці слова були вигравірувані на пам’ятній медалі, яка була випущена в рік смерті Гаусса (1855).
Гаус був тоді ще дитиною, хоч і дуже розумним розвинутим не по роках.
Перший виступ
Задача № 1
Відома теорема: сума членів скінченної арифметичної прогресії дорівнює добутку півсуми її крайніх членів на число членів прогресії.
Можна довести геометрично.
При цьому ми будемо вважати, що а![]() >о і d>0.
>о і d>0.
![]()
a
![]()
![]()
![]()
![]() d Q
d Q
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() d d
d d
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() d
d
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() d d
d d
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() d
d
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() d
d ![]()
![]()
![]()
![]() R a
R a![]() a
a![]() a
a![]()
![]() P
P
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() O n
O n
1 2 3 4 n
Мал. 1.
Із малюнка 1 зрозуміло, що числа a![]() , a
, a![]() , ..., а
, ..., а![]() дають по порядку
дають по порядку
(а![]() ), зображених на малюнку прямокутників, і, отже, сума
), зображених на малюнку прямокутників, і, отже, сума
S![]()
дорівнює площі всієї ступінчатої фігури. Але ту ж саму площу можна дістати, якщо до площі трапеції ОРQR додати n площу прямокутних трикутників з катетами 1 і d (на малюнку 1 ці трикутники заштриховані).
![]() =
=![]()
Це і є потрібний результат.
Нестандартні задачі – це такі, які в курсі математики не мають загальних правил і положень, що визначають точну програму їх розв’язання.
Задача № 2
Знайти суму:
а) -100 – 99 – 98 – 97 - ... – 1+1+ 2 +... + 100 + 101 +102.
Відповідь. 203.
б) 1 +2 – 3 – 4 + 5 +6 – 7 – 8 + 9 +10 – 11 – 12 + 13 + 14 - ... + 301 + 302.
Розв’язання:
1 + ( 2 – 3 – 4 +5) + ( 6 – 7 – 8 + 9) + (10 – 11 – 12 +13) +... + (298 – 299 – 300 + +301) + 302 = 303, оскільки сума цифр у кожній дужці дорівнює нулю.
Другий виступ
Властивості трикутників, сторони яких утворюють арифметичну прогресію.
Трикутник, сторони якого утворюють арифметичну прогресію, називається різницевим (різниця – елемент, що характеризує арифметичну прогресію). Позначимо довжини сторін такого трикутника через а, в, с і, не обмежуючи загальності, вважатимемо, що в>а >с, тобто а = ![]() .
.
Задача. У різницевому трикутнику котангенси половин кутів, трикутника становлять арифметичну прогресію. Довести.
Доведення.
Неважко показати, що в усякому трикутнику
(Мал.2) AK![]() =p-a, ВК
=p-a, ВК![]() =р-в, СК
=р-в, СК![]() , К
, К![]() К
К![]()
А – точки дотику вписаного в

![]() трикутник кола до його сторін).
трикутник кола до його сторін).

![]()
![]() Якщо довжини сторін а, в, с є членами
Якщо довжини сторін а, в, с є членами
 арифметичної прогресії, то числа p-a, р-в,
арифметичної прогресії, то числа p-a, р-в,
р-с, а отже, й числа ![]() ,
, ![]()
![]() теж є
теж є
В С членами арифметичної прогресії. Але
К![]()
![]() = сtg
= сtg![]() ,
, ![]() = сtg
= сtg ![]() ,
, ![]() = сtg
= сtg![]() .
.
Третій виступ
Відомі задачі про:
- поділ хліба
- поливання городу
- годівля курей
- бригада землекопів
- яблука
- купівля коня
- винагорода воїна
Задача. Яблука.
Садівник продав першому покупцеві половину усіх своїх яблук і ще пів – яблука, другому покупцеві – половину залишених і ще пів – яблука; третьому – половину залишених і ще пів – яблука і т. д. Сьомому покупцеві він продав половину залишених яблук і ще пів – яблука; після цього яблук у нього не залишилось. Скільки яблук було у садівника?
Розв’язання:
Якщо початкове число яблук х, то перший покупець одержав
![]()
другий ![]()
третій ![]()
... .... ... ... ... ... ... ... ... ...
Сьомий покупець одержав ![]() .
.
Маємо рівняння
![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]()
або (![]() +1)(
+1)( ![]() +
+![]() +
+![]() +…+
+…+![]() )=
)=![]() .
.
Обчислюючи суму членів геометричної прогресії, яка стоїть у дужках, знаходимо:
![]()
![]() .
.
Усіх яблук було 127.
Алгебра на клітчастому папері
Незважаючи на п’ятдесятивікову давність цієї задачі на прогресії, у нашому шкільному ужитку прогресії з’явилися порівнюючи недавно. У підручнику Магницького, який був виданий двісті років тому і цілих півстоліття був основним посібником для шкільного навчання, прогресії хоч і є, але загальних формул, які зв’язують величини, що входять до них, в ньому не подано. Сам укладач підручника не без труднощів справлявся з такими задачами. А проте формулу суми членів арифметичної прогресії легко вивести простим і наочним способом за допомогою клітчастого паперу. На такому папері будь – яка арифметична прогресія зображується ступінчастою фігурою. Наприклад, фігура АВСД на мал. 3 зображує прогресію 2; 5; 8; 11; 14 і т. д.
Щоб визначити суму її членів, доповнимо креслення до прямокутника АВGE. Одержимо дві рівні фігури АВДС і ДGЕС. Площа кожної з них зображує суму членів нашої прогресії. Отже, подвійна сума прогресії дорівнює площі прямокутника АВGЕ, тобто (АС + СЕ) АВ.
|
B
A |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
1 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
E |
Мал. 3.
Однак АС + СЕ зображує суму 1 – го і 5 – го членів прогресії, АВ – число членів прогресії. Тому подвійна сума
![]() (сума крайніх членів)(число членів) або S=
(сума крайніх членів)(число членів) або S=![]()
Четвертий виступ
Задача № 1.
Скільки пар кроликів народиться за рік від однієї пари, якщо кожна пара дає щомісяця приплоду по одній парі, яка в свою чергу здатна до розмноження через один місяць, і якщо жодна пара не загине?
На початку року маємо 1 пару кролів, через місяць їх буде – 2 пари, через два місяці – 3, через три – 5, потім через кожний місяць кролів буде відповідно 8, 13, 21, 34, 55, 89, 144, 233 і, нарешті, 377 пар, а всього 986 пар.
Розв’язання задачі привело до цікавої рекурентної числової послідовності:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,..., ![]()
![]() =
= ![]()
![]()
![]() +
+![]()
![]()
![]() . Французький математик Едуард Люка ( 1842 – 1891) назвав послідовності, члени яких утворюються за таким рекурентним законом, рядами, або послідовностями Фібоначчі, а їх члени – числами Фібоначчі, які постають при розв’язуванні численних практичних і теоретичних задач і мають багато цікавих властивостей. Зокрема, суму перших n послідовних чисел Фібоначчі можна обчислити за формулою:
. Французький математик Едуард Люка ( 1842 – 1891) назвав послідовності, члени яких утворюються за таким рекурентним законом, рядами, або послідовностями Фібоначчі, а їх члени – числами Фібоначчі, які постають при розв’язуванні численних практичних і теоретичних задач і мають багато цікавих властивостей. Зокрема, суму перших n послідовних чисел Фібоначчі можна обчислити за формулою:
![]()
![]() +
+![]()
![]() +...+
+...+![]()
![]() =
=![]()
![]()
![]() -1
-1
У XІІІ ст. італійський математик Л.Пізанський (Фібоначчі) (1170 – 1250) досліджував послідовність
1, 1, 2, 3, 5, 8, 13, 21, ...,
кожний член якої, починаючи з третього, дорівнює сумі двох попередніх членів. Кілька століть математики не могли знайти її n –й член. Тепер він відомий:
![]() =
=![]()
Задача № 2
Розв’язати рівняння:
![]() +
+![]() =
= ![]() де
де ![]() <1
<1
Розв’язання:
![]() +
+ ![]() -
- ![]() = 0.
= 0.
![]()
![]()
D=81![]() 9
9![]() =81-72=9, D>0.
=81-72=9, D>0.
![]()
![]()
![]()
Відповідь: ![]() Вказівка. Використати суму
Вказівка. Використати суму ![]()
П’ятий виступ
Правила для знаходження суми членів геометричної прогресії є в «Началах» Евкліда. Архімед вивів правила для знаходження суми квадратів перших n натуральних чисел, вмів він також обчислювати суми членів нескінченних спадних геометричних прогресій.
Історичні відомості
Приклади окремих арифметичних і геометричних прогресій можна зустріти ще в давньовавілонських та єгипетських надписах, які мають вік біля чотирьох тисячоліть і більше. В давній Греції ще за п’ять століть до н. е. були відомі такі суми:
1 + 2 + 3 + ... + n = ![]() ,
,
1 + 3 + 5 + ... + (2n-1) = ![]() ,
,
2 + 4 + 6 + ... + 2n = n ( n + 1).
Математики давньої Індії та Китаю складали і розв’язували різні задачі на арифметичні та геометричні прогресії. У європейців правило для знаходження суми членів будь- якої арифметичної прогресії зустрічається вперше в роботі Леонарда Пізанського «Книга про абака» (1202). У давньогрецьких математиків вивчення геометричних прогресій починається від так званої неперервної геометричної пропорції, тобто пропорції виду
а : х = х : с ; тут х = ![]() – середнє пропорційне між а і с. Очевидно, що числа а,
– середнє пропорційне між а і с. Очевидно, що числа а, ![]() , с утворюють геометричну прогресію із трьох членів з першим членом, рівним а, знаменником q =
, с утворюють геометричну прогресію із трьох членів з першим членом, рівним а, знаменником q =![]() Її можна записати в вигляді: а, аq, аq
Її можна записати в вигляді: а, аq, аq![]() і продовжувати дальше аq
і продовжувати дальше аq![]() , аq
, аq![]() , .... .
, .... .
У вже згаданій роботі Евкліда «Начала» (близько 300 років до н.е.) в
словесній формі міститься теорема відносно геометричної прогресії, яку можна виразити слідуючою рівністю:
![]()
Звідси одержуємо: ![]()
Легко переконатися, що цей результат тільки по зовнішньому вигляду відрізняється від результату![]() . Насправді,
. Насправді, ![]() і, отже:
і, отже:
![]() .
.
Тому формула Евкліда може бути подана в слідуючому знайомому вигляді:
![]() .
.
Відома задача про нагороду, яка була присвоєна за винахід шахматної гри, зустрічається вперше у хорезмського математика – ал – Біруні (973 – 1048). Мова іде тут про кількість зернин, яка одержиться якщо на першу клітку шахматної дошки покласти зерно пшениці, на другу – 2, на третю - 2![]() , на четверту - 2
, на четверту - 2![]() і т.д., на останню шістдесят четверту - 2
і т.д., на останню шістдесят четверту - 2![]() . Підрахунок кількості всіх зернин зводиться до знаходження суми:
. Підрахунок кількості всіх зернин зводиться до знаходження суми:
1 + 2 +2![]() + ... +2
+ ... +2![]() = 2
= 2![]() – 1.
– 1.
В словесній формі загальне правило для знаходження суми членів будь-якої скінченної геометричної прогресії зустрічається у французського математика Шюке (1484).
Сума нескінченно спадної геометричної прогресії
1 + ![]() +
+ ![]() +
+![]() +...+
+...+![]() +...=2 використовується Архімедом (287 – 212 рр. до н. е.) для обчислення площі сегменту обмеженого параболою. Загальна формула для знаходження суми будь –якої нескінченної спадної геометричної прогресії була виведена в першій половині XVІІ ст. декількома математиками ( і серед них французьким математиком П’єром Ферма). Відмітимо, накінець, що формула для суми квадратів натуральних чисел:
+...=2 використовується Архімедом (287 – 212 рр. до н. е.) для обчислення площі сегменту обмеженого параболою. Загальна формула для знаходження суми будь –якої нескінченної спадної геометричної прогресії була виведена в першій половині XVІІ ст. декількома математиками ( і серед них французьким математиком П’єром Ферма). Відмітимо, накінець, що формула для суми квадратів натуральних чисел: ![]() була відома ще Архімеду, який користувався нею , при розв’язуванні задач геометрії і механіки.
була відома ще Архімеду, який користувався нею , при розв’язуванні задач геометрії і механіки.
1. Знайдіть суму: 1 + 9 + 25 + ... + ( 2n – 1)![]() .
.
Розв’язання:
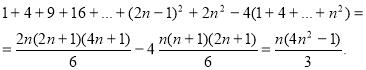
2. Знайти суму:
1![]()
Розв’язання:
Запишемо загальний член цього ряду так:
а![]() ,
,
тоді задана сума набирає вигляду
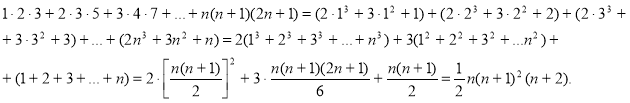 Відповідь:
Відповідь: ![]()
3. Для будь – яких n ( n є N) справджується рівність:
![]() ... .
... .
Відомо, що ![]() Звідки
Звідки ![]() Але
Але ![]() тому
тому 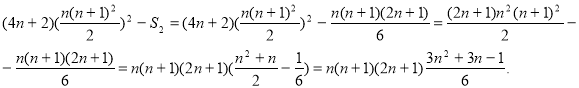
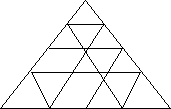
4. Піраміду із тенісних м’ячів можна скласти і іншим способом. Почнемо з шару в... м’ячів, розміщених у вигляді квадрата, як це показано на мал. 4;

![]()
Мал. 4.
На нього вкладіть другий шар із м’ячів, потім третій шар із ... м’ячів і т.д. і накінець на самому верху – останній м’яч. Скільки всього м’ячів міститься в такій піраміді?
1![]()
Шостий виступ
Графіки членів прогресії і їх сум
Графіками членів прогресії є множина точок, розміщених на графіку лінійної функції у = к х + в, якщо прогресія арифметична, і на графіку
у = Аq![]() , якщо прогресія геометрична.
, якщо прогресія геометрична.
Порівняємо тепер ці графіки з графіками сум n перших членів прогресії – спочатку арифметичної, потім геометричної.
Розглянемо окремі приклади.
-
Нехай дано арифметичну прогресію з загальним членом a
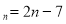 . Сума її n членів
. Сума її n членів 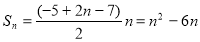 . являє собою квадратичну функцію
. являє собою квадратичну функцію 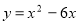 при х = n =1, 2, 3, ... .
при х = n =1, 2, 3, ... .
![]()
![]() Отже, графіком S
Отже, графіком S![]() є множина окремих точок, розміщених на параболі
є множина окремих точок, розміщених на параболі ![]() . На малюнку 5 зображений графік членів прогресії ( точки, які лежать на прямій у = 2 х – 7 , при х = n = 1, 2, 3, ... .) і графік
. На малюнку 5 зображений графік членів прогресії ( точки, які лежать на прямій у = 2 х – 7 , при х = n = 1, 2, 3, ... .) і графік ![]() .
.
16
![]() 14
14


12
![]()
![]()
![]()
![]() 10 S
10 S![]() a
a![]()
![]() d
d
8
![]()
6
![]() 4
4
![]() 2
2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() O n
O n
![]() 1 2 3 4 5 7 8 9 10
1 2 3 4 5 7 8 9 10
-2
![]() -4
-4
![]() -6
-6
-8
![]()
![]() -10
-10
Мал. 5.
При збільшенні n відповідні точки параболи піднімаються все вище і вище; тим самим наочно підтверджується зроблений нами висновок:
завжди можна знайти таке n, щоб ![]() перевищить по абсолютній величині будь – яке наперед задане додатне число.
перевищить по абсолютній величині будь – яке наперед задане додатне число.
- Нехай тепер дано геометричну прогресію:
1, 2, 4, 8, 16, ... ( q = 2). Її загальний член ![]() і
і ![]() =
=![]() .
.
Графік членів – множина точок, які лежать на графіку функції ![]() при х = n = 1, 2, 3... . Графік
при х = n = 1, 2, 3... . Графік ![]() – множина точок, які належать графіку функції
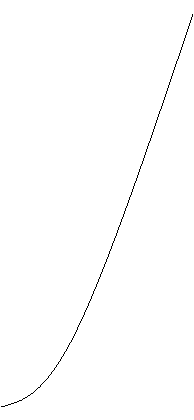
– множина точок, які належать графіку функції ![]() при х= n = 1, 2, 3,...( мал.6); для наглядності за одиницю приймемо відрізок, в 2 рази менший, ніж по осі абсцис). На цих графіках також ясно видно, що при необмеженому збільшенні n при q...1 сума n членів геометричної прогресії необмежено зростає.
при х= n = 1, 2, 3,...( мал.6); для наглядності за одиницю приймемо відрізок, в 2 рази менший, ніж по осі абсцис). На цих графіках також ясно видно, що при необмеженому збільшенні n при q...1 сума n членів геометричної прогресії необмежено зростає.
![]()
![]()
 32 U
32 U![]()
![]() 30 S
30 S![]()
![]() 28
28
![]() 26
26
![]() 24
24
22
![]()
![]() 20
20
![]() 18
18
![]() 16
16
![]() 14
14
![]() 12
12
![]() 10
10
![]() 8
8
6
![]()
![]() 4
4
![]() 2
2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
O 1 2 3 4 5 6 n
Мал. 6.
-
Якщо 0<q<1 і
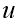
 >0, то графіки
>0, то графіки 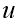
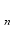 і
і 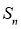 будуть іншими.
будуть іншими.
Розглянемо це на прикладі прогресії:
1, ![]() В цьому випадку
В цьому випадку ![]()
![]() =
=![]() і
і ![]() =2-
=2-![]() . Відповідні графіки дано на мал. 149; тут на осі ординат за 1 прийнято відрізок, в 8 разів більший, ніж по осі абсцис.
. Відповідні графіки дано на мал. 149; тут на осі ординат за 1 прийнято відрізок, в 8 разів більший, ніж по осі абсцис.
На графіках ясно видно, що із збільшенням n,
![]()
![]()
![]()
![]() 0, а
0, а ![]() 2.
2.
Сьомий виступ
Важливе значення мають два способи задання послідовностей – явною формулою загального члена й рекурентною формулою.
Рекурентний спосіб задання послідовності більш специфічний. Він істотно зв’язаний саме з тим, що послідовність – функція натурального аргументу.
Задача 1. Послідовність ![]() задано рекурентно:
задано рекурентно: ![]()
Знайти загальний член послідовності.
Розв’язання. Маємо:
![]()
![]()
На основі одержаних рівностей висловлюємо гіпотезу: загальний член послідовності визначається рівністю
![]() (1)
(1)
Доведемо гіпотезу методом математичної індукції. Дійсно, при n=1 рівність (1) правильна. Нехай вона є правильною при n=k, тобто ![]() . Доведемо її правильність при n=k+1. Тоді
. Доведемо її правильність при n=k+1. Тоді
![]() .
.
Отже, рівність (1) є правильною для будь-якого n.
Задача 2. Послідовність ![]() задано рекурентно:
задано рекурентно:
![]()
Знайти загальний член послідовності.
Розв’язання. Бачимо, що
![]()
Висловлюємо гіпотезу, що ![]() Доведемо гіпотезу методом математичної індукції. При n=1 твердження правильне. Нехай воно правильне при
Доведемо гіпотезу методом математичної індукції. При n=1 твердження правильне. Нехай воно правильне при ![]() доведемо, що воно правильне при n=k+1, тоді
доведемо, що воно правильне при n=k+1, тоді
![]()
Таким чином, ![]()
Зазначимо, що в результаті спостережень можна зробити й неправильний висновок. Наприклад, розглянено множину чисел
![]()
де n- довільне натуральне число. Для n=1,2,3,4 одержимо відповідно m=5,11,19,29, тобто перші чотири значення m – прості числа. Чи можна стверджувати на основі одержаних спостережень, що для будь-якого натурального n число m буде простим? Ні. Наприклад, при n=6 число m=55 є складеним.
V. Підсумок уроку:
- Що нового ви дізналися?
- Під час виконання яких завдань у вас виникали труднощі?
- Над чим нам потрібно ще працювати?
- Чи вдалося вам виконати на уроці те, що ви хотіли?
- Що сприяло успіху в роботі? Що заважало?
Як приємно дізнатися, що ти чогось дізнався.
Ж. Мольєр.
Впевнена, що ви зрозуміли необхідність набуття знань з математики.
Мені хочеться закінчити наш урок словами М.І. Калініна: «Яку б науку ти не вивчав, в який би ВНЗ не поступав, в якій би галузі не працював, якщо ти хочеш залишити слід, то для цього всюди необхідне знання математики… Наповнюй свою голову математикою, поки є можливість. Вона потім надасть величезну допомогу у всій вашій роботі». Україні потрібні хороші спеціалісти: інженери, архітектори, потрібні навіть керівники державою.
VІ. Домашнє завдання:
Домашнє завдання сьогодні носить творчий характер і допоможе вам закріпити здобуті на уроках знання.
Чому дорівнює сума чисел у n – му рядку «арифметичного трикутника»?
1
2 + 3
4 + 5 + 6
7 + 8 + 9 + 10
11 + 12 + 13 + 14 + 15
…………………………. ?
![]()
|
А. |
Б. |
В. n ( n |
Г. Інша відповідність |
Розв’язання:
Існує певна закономірність для перших доданків сусідніх рядків:
2 – 1 = 1, 4 – 2 = 2, 7 – 4 = 3, 11 – 7 = 4, …
Ця закономірність пов’язана з тим, що кількість доданків у рядку дорівнює номеру рядка. Якщо позначимо перший доданок n – го рядка через а![]() , то маємо:
, то маємо:
а![]() - а
- а![]() = n – 1 або а
= n – 1 або а![]() = а
= а![]() + n - 1
+ n - 1
Звідси
а![]() = 1 + 1 + 2 + … + (n – 1) = 1 +
= 1 + 1 + 2 + … + (n – 1) = 1 + ![]() .
.
У n – му рядку n доданків. Таким чином, сума чисел S![]() у n – му рядку дорівнює:
у n – му рядку дорівнює:
S![]() =
= ![]() + 1 +
+ 1 + ![]() + 2 + … +
+ 2 + … + ![]() + n =
+ n = ![]() +
+ ![]() =
= ![]() (n
(n![]() - n
- n![]() + n
+ n![]() + n) =
+ n) = ![]()
Відповідь. А. ![]() .
.
Література:
1. Я.І. Перельман. Цікава алгебра. Видавництво «Техніка». К. 1973, с.161
2. В.Я. Валах. Подорож у світ цілих чисел. К, 1978. с. 4.
3. А.Г. Конфорович. Визначні математичні задачі. 1981, с.100.
4. Ш.Г. Горделадзе, М.М. Кухарчук, Ф.П. Яремчук. Збірник конкурсних задач з математики. Видавництво «Вища школа», К. 1976; с. 43.
5. В.М. Алєксєєв. Елементарна математика. Видавництво «Вища школа». К. 1983. с. 46.
6. А.Я. Дороговцев. Вибрані задачі з математичного аналізу. К. «Вища школа» 1982; с. 11.
7. В.А. Вишенський, М.О. Перестюк, А.М. Самойленко. Збірник задач з математики. К. «Либідь», 1990; с. 22.
8. У світі математики. Випуск 5. К. – 1974; с. 152.
9. А.І. Маркушевич, К.П. Сикорський, Р.С. Черкасов Алгебра і елементарні функції. Видавництво «Просвітництво». 1968. с. 284.
10. Д. Пойа. Математичне відкриття. Видавництво «Наука» 1976; с. 85.


про публікацію авторської розробки
Додати розробку
