Урок -лекція "Показникова фукція"

Вид заняття  - лекція

Тема: Показникова функція, її графік та властивості.

Мета заняття : формування уявлень про показникову функцію, її властивості; навчити будувати ескіз графіка показникової функції і «читати по графіку властивості функції»; розвивати пізнавальний інтерес, виховувати інформаційну культуру; розвивати алгоритмічне мислення, уважність. інтерес  до предмету; виховувати культуру спілкування.

Методи : словесні, інтерактивний, особистісно-орієнтований, практичні. Матеріально-технічне забезпечення та дидактичні засоби, ТЗН: таблиця, роздатковий матеріал, геометричні приладдя

Література додаткова, основна: 1) Алгебра і початки аналізу: підручник для 10 кл. загальноосвіт. навч. закладів/   М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук;.  – К.: Зодіак – ЕКО, 2003. -  272 с.

2) А.Г.Мерзляк, «Збірник задач і завдань для тематичного оцінювання з алгебри і початків аналізу для 10 класу». –Харків, Гімназія»,2001

 Структура заняття                                    відведений час

1. Організаційна частина:  контроль відвідування                                     3 хв

2. Актуалізація опорних знань:                                                                     25 хв

• Контроль виконання домашнього завдання;
• Аналіз РКР
• Усне розв'язування ірраціональних рівнянь, основні типи рівнянь (таблиця). Самостійна робота на картках (перевірка навичок розв’язування ірраціональних рівнянь)

3. Повідомлення теми, формування мети та основних                              2 хв

завдань

4. Мотивація навчальної діяльності                                                              5 хв

Більшість процесів у життя пов’язано із залежністю між величинами. Наприклад, кількість виконаної роботи залежить від її обсягу та складності самої роботи, рівень знань учня від рівня його інтелектуального розвитку вартість покупки від кількості купленого товару і цін. Одна залежність носить випадковий характер, інші постійні.  Давайте розглянемо наступні закони.

 1. Закон радіоактивного розпаду. Також є закон, який дає нам можливість визначити, скільки радіоактивних ядер з часом розпадеться.За законом радіоактивного розпаду за одиницю часу з наявної кількості радіоактивних ядер завжди розпадеться їх частина, яка є сталою величиною. Вона називається сталою розпаду даного елемента і позначається літерою λ. Цей закон можна записати таким чином: , де N₀ – початкова кількість атомів; t – час розпаду; T – період піврозпаду (тобто час, за якого кількість атомів ядра елемента зменшується вдвоє, він є сталою величиною для кожного елемента); N – кількість атомів, які не розпались.

2. Зростання деревини відбувається за законом    : 

A- зміна кількості деревини в часі;
А₀ - початкова кількість деревини;
t- час, а, к- деякі постійні.
3. Тиск повітря убуває з висотою згідно із законом :
P- тиск на висоті h;
P₀- тиск на рівні моря;
а- деяка постійна.

4. Охолодження води у чайнику відбувається за експоненціальним законом: T=T₀ ∙a^-kt, де  T₀ – температура кипіння води; t – час; a, k – деякі сталі.

- Що спільного в цих  процесах?

( Студенти відповідають, відзначаючи схожість виду формули, яка задає закон). Припустимо, що в цих формулах А₀=1, P₀=1, к=1, яку функцію отримаємо? ().
        Така функція називається показниковою. І сьогодні на занятті, ми повинні дати означення показникової функції, розглянути деякі властивості і навчиться застосовувати ці властивості при виконанні завдань, певного вигляду.

5. Вивчення матеріалу за планом:                                                                   30 хв

1. Означення показникової функції.

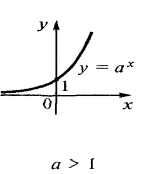
2. Властивості і графік показникової функції з основою a > 1.

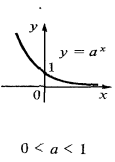
3. Властивості і графік показникової функції з основою  0 < a < 1.

Показникова функція, її властивості і графік

6. Узагальнення матеріалу:                                                                           10хв      

        А.Г.Мерзляк:  впр.185(2,3), врп.186 (усно),187 (усно) ,188(усно)                                                                                                                                                                                                                   

7. Підведення підсумків:                                                                                 5хв

  Інтерактивна вправа «Незакінчене речення» у поєднання з «Мікрофоном». (викладач формулює незакінчене речення і пропонує студентам висловитися щодо підсумку уроку, закінчуючи його. Кожний наступний студент повинен починати свій виступ із запропонованої формули. Відповідають студенти по черзі за допомогою «мікрофону» (ручка, олівець).

Студенти працюють з відкритими реченнями:

«Сьогодні на занятті ми дізналися про…»

«При а>1 показникова функція має наступні властивості…»

«Якщо 0<a<1, то виділяємо властивості показникової функції..»

«При розв’язування вправ я застосовую наступні основні властивості степенів…»

«На занятті я відкрив для себе…»                                                                                                                     

8. Видача завдання для самостійної роботи студентів:    Основна [7], §.1,розд.IV, пит. 1-11