Урок 11. "Нерівності з однією змінною"

УРОК № 11

Тема уроку. Нерівність з однією змінною

Мета уроку: засвоєння учнями змісту понять: нерівність з однією змінною, розв'язок нерівності з однією змінною та що означає розв'язати нерівність з однією змінною; які нерівності називають рівносильними.  Виробити в учнів уміння: відтворювати зміст вивчених понять і використовувати їх для розв'язування завдань. Розвивати почуття прекрасного, потяг до нових знань. Виховувати почуття  відповідальності  у навчанні, толерантність.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання: опорний конспект, презентація, проектор, комп’ютер.

Хід уроку

Нерівність - заява про незгоду з ким,  чим-небудь,  доказ проти чогось.

«Словник української мови»

I. Організаційний етап

Перевірка готовності до уроку, налаштовує учнів на роботу.

II. Перевірка домашнього завдання

На початку уроку вчитель збирає на перевірку зошити з виконаним домашнім завданням (якщо таке було задано). Відповісти на запитання учнів за темою. 

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів.

Вчитель. Ви вже можете розв’язувати рівняння виду 6х – 8 = 21. Нагадаємо алгоритм (учні відповідають). Якщо замість знака рівності поставити знаки нерівності, нагадайте ці знаки, то отримаємо що, на вашу думку? Вірно, нерівності. Ці нерівності містять що? Змінну, вірно. Тому такі нерівності і називають нерівностями з однією змінною і наше завдання ввести поняття таких нерівностей.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1.   Коли число а більше від числа b; менше від числа b? (Дайте означення, наведіть приклади.)

2.   Як розміщені на координатній прямій точки, що відповідають числам а і b, якщо а  b? Наведіть приклади.

3.   Які нерівності називають строгими? нестрогими? Наведіть приклади.

4.   Сформулюйте властивості числових нерівностей. Наведіть приклади.

5.   Сформулюйте властивість про почленне додавання нерівностей. Наведіть приклади.

6.   Сформулюйте властивість про почленне множення нерівностей. Наведіть приклади.

7.   Сформулюйте наслідки з властивостей числових нерівностей. Наведіть приклади.

 V. Формування знань

План вивчення нового матеріалу

1.   Уявлення про нерівність з однією змінною.

2.   Розв'язок нерівності з однією змінною та що означає розв'язати нерівність з однією змінною.

3. Рівносильні нерівності.

Опорний конспект

Історична довідка

Знаки нерівності (строгі знаки)>, <─ з'явилися вперше в 1631 році, але саме поняття нерівності, виникло в глибокій давнині. А ввів, уживані понині знаки нерівності, англійський учений Гарріот. Символи ≥, ≤ (нестрогі знаки нерівності) введені в 1734 році французьким математиком П'єром Бузі. У розвитку математичних міркувань без порівняння величин, без понять «більше» і «менше» не можна було дійти до поняття рівності, тотожності, рівняння.

VI. Формування вмінь

Усні вправи

1.   Знайдіть значення виразу:

1) 2х – 1 при х = 2; 0,2;                       

2) 4х + 5 при х = 2; 0,2.

2.   Чи буде правильною нерівність:

1) 3х – 5 > 0 при х = -1; 2; 1,5  

2) 5 – 0,2х < 7 при х = 0; -10; -100?

3.   Назвіть:

1) найменше ціле число, що задовольняє нерівність -2 < х < 3;

2) найменше натуральне число, що задовольняє нерівність -2 < х < 3;

3) найбільше натуральне число, що задовольняє нерівність -2 < х < 3.

4.   Чи є число -3 коренем рівняння:

1) х + 3 = 0;               

2) (х + 3)(x – 7) = 0;   

3) х³ – 3х + 18 = 0?

 За підручником А.Г. Мерзляк № 4.1; 4.2; 4.4; 4.7.

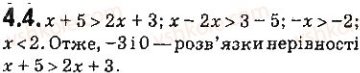
Письмові вправи

VII. Підсумки уроку

Контрольне запитання

Яке з чисел: х = 1; х = 4; х = 5 — є розв'язком:

1. нерівності 2x – 3 < 5.

Говорячи про нерівність, як про математичне поняття, хочеться внести до нашого уроку деякого присмаку і тим самим заперечити той факт, що математика суха та нудна наука. Поєднати  і порівняти на перший погляд   різні предмети, наприклад алгебру та літературу. Послухайте як почуває себе «нерівність» в поезії.

Нерівність душ

Нерівність душ страшніша всіх розлук,

Нерівність душ-це бачиш різне сонце.

Але не відчуваєш його рук,

Хоч дивишся завжди в одне віконце.

Нерівність душ-це гірше,ніж тримать

В руках якесь розпечене залізо.

Нерівність душ потрібно признавать

Тоді,коли іще не буде пізно.

Нерівність душ-це різніі світи,

Це різне небо,навіть різні хмари.

Молю,цим свою душу не топчи,

І відпусти примарливі лиш чари... 

 Віда Вансель

VIII. Домашнє завдання

1.   Вивчити зміст понять, розглянутих на уроці п. 4 підручника

2.   Виконати вправи на закріплення вивчених понять і способів дій (аналогічні за змістом вправам класної роботи).

3.   На повторення: вправи на відновлення вмінь застосовувати властивості числових нерівностей та рівняння з модулем.

4. №№ 4.6; 4.8; 4.10.