Властивості опуклих чотирикутників,які вивчає планіметрія

ПАРАЛЕЛОГРАМИ, ЇХ ВИДИ ТА ВЛАСТИВОСТІ

1. Паралелограм та його властивості

     Паралелограмом називають чотирикутник, у якого протилежні сторони попарно паралельні.

    Наприклад: чотирикутник ABCD – паралелограм, оскільки .

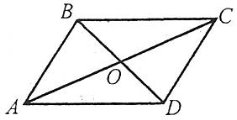
Властивості паралелограма

У паралелограма:

1. Протилежні сторони рівні. AB=CD, AD=BC.
2. Протилежні кути рівні. .
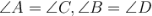3. Діагоналі точкою перетину діляться навпіл. АО=ОС, ВО=ОD.
4. Кожна діагональ розбиває паралелограм на два рівних трикутники. .
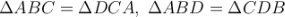5. Сума кутів, прилеглих до однієї сторони паралелограма, дорівнює 180°. .
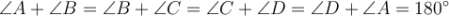6. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін: 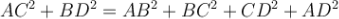 або .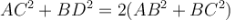

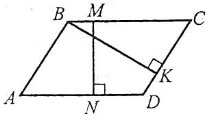
     Висотою паралелограма називають перпендикуляр, опущений із будь-якої точки однієї сторони на пряму, що містить протилежну сторону (або відстань між протилежними сторонами).

    Наприклад: MN і ВК – висоти.

Ромб — це паралелограм, який має рівні сторони. Якщо у ромба всі кути прямі, тоді він називається квадратом.

Ромби відрізняються між собою за сторонами та кутами.

 

Основні властивості ромба

1. Має всі властивості паралелограма

2. Діагоналі перпендикулярні:

AC┴BD

3. Діагоналі є бісектрисами кутів ромба:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Сума квадратів діагоналей рівна квадрату сторони, помноженому на чотири:

AC² + BD² = 4AB²

5. Точка перетину діагоналей називається центром симетрії ромба.

6. В будь-який ромб можна вписати коло.

7. Центром кола, вписаного в ромб, буде точка перетину його діагоналей.

Квадрат - це чотирикутник, у якого всі чотири сторони та кути однакові. Квадрати відрізняються між собою тільки довжиною сторони, але всі чотири кути у них прямі, тобто по 90°.
Основні властивості квадрату

Квадратом також можуть бути паралелограм, ромб або прямокутник якщо вони мають однакові довжини діагоналей, сторін та однакові кути.

1. Всі чотири сторони квадрата мають однакову довжину, тобто вони рівні:

AB = BC = CD = AD

2. протилежні сторони квадрата паралельні:

AB||CD,   BC||AD

3. Всі чотири кути квадрата прямі:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Сума кутів квадрата дорівнює 360 градусів:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. Діагоналі квадрата мають однакової довжини:

AC = BD

6. Кожна діагональ квадрата ділить квадрат на дві однакові симетричні фігури

7. Діагоналі квадрата перетинаються під прямим кутом, і розділяють одна одну навпіл:

AC┴BD		AO = BO = CO = DO =	d
			2

8. Точка перетину діагоналей називається центром квадрату і також є центром вписаного та описаного кола

9. Кожна діагональ ділить кут квадрату навпіл, тобто вони є бісектрисами кутів квадрату:

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

10. Обидві діагоналі розділяють квадрат на чотири рівні трикутника, до того ж ці трикутники одночасно і рівнобедрені, і прямокутні:

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Прямокутник - це чотирикутник, у якого дві протилежні сторони рівні і всі чотири кути однакові.
Основні властивості прямокутника

Прямокутником можуть бути паралелограм, ромб або квадрат.

1. Протилежні сторони прямокутника мають однакову довжину, тобто вони рівні:

AB = CD,   BC = AD

2. Протилежні сторони прямокутника паралельні:

AB||CD,   BC||AD

3. Прилеглі сторони прямокутника завжди перпендикулярні:

AB _┴ BC,   BC _┴ CD,   CD _┴ AD,   AD _┴ AB

4. Всі чотири кути прямокутника прямі:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. Сума кутів прямокутника дорівнює 360 градусів:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Діагоналі прямокутника мають однакової довжини:

AC = BD

7. Сума квадратів діагоналі прямокутника дорівнюють сумі квадратів сторін:

2d² = 2a² + 2b²

8. Кожна діагональ прямокутника ділить прямокутник на дві однакові фігури, а саме на прямокутні трикутники.

9. Діагоналі прямокутника перетинаються і в точці перетину діляться навпіл:

		AO = BO = CO = DO =	d
			2

10. Точка перетину діагоналей називається центром прямокутника, а також є центром описаного кола

11. Діагональ прямокутника є діаметром описаного кола

12. Навколо прямокутника завжди можна описати коло, бо сума протилежних кутів дорівнює 180 градусів:

∠ABC + ∠CDA = 180°   ∠BCD + ∠DAB = 180°

13. В прямокутник, у якого довжина не дорівнює ширині, не можна вписати коло, бо суми протилежних сторін не рівні між собою (вписати коло можно тільки в частинний випадок прямокутника - квадрат).

Трапеція — це чотирикутник, у якого дві сторони паралельні, а дві інші сторони не паралельні.

Паралельні сторони називаються основами трапеції, а дві інші боковими сторонами

Також, трапецією називається чотирикутник, у якого одна пара протилежних сторін паралельна, але сторони не рівні між собою.

Елементи трапеції:

• Основи трапеції - паралельні сторони
• Бокові сторони - дві інші сторони
• Середня лінія - відрізок, що з'єднує середини бокових сторін.

Види трапецій:

• Рівнобедрена трапеція - трапеція, у якої бокові сторони рівні
• Прямокутна трапеція - трапеція, у якої одна із бокових сторін перпендикулярна основам.

Основні властивості трапеції

1. В трапецію можна вписати коло, якщо сума довжин основи рівна сумі довжин бокових сторін:

AB + CD = BC + AD

2. Середня лінія трапеції розділяє навпіл будь-який відрізок, який з'єднує основи,а також ділить навпіл діагоналі:

AK = KB, AM = MC, BN = ND, CL = LD

3. Середня лінія трапеції паралельна основам і рівна їх півсумі:

m =	a + b
	2

4. Точка перетину діагоналей трапеції і середини основ лежать на одній прямій.

5. В трапеції бокову сторону видно із центра вписаного кола під кутом 90°.

6. Кожна діагональ в точці перетину ділиться на дві частини з таким співвідношенням довжини, як співвідношення між основами:

BC : AD = OC : AO = OB : DO

7. Діагоналі трапеції d₁ і d₂ пов'язані зі сторонами співвідношенням:

d₁² + d₂² = 2ab + c² + d²

Основні властивості трапеції

1. В трапецію можна вписати коло, якщо сума довжин основи рівна сумі довжин бокових сторін:

AB + CD = BC + AD

2. Середня лінія трапеції розділяє навпіл будь-який відрізок, який з'єднує основи,а також ділить навпіл діагоналі:

AK = KB, AM = MC, BN = ND, CL = LD

3. Середня лінія трапеції паралельна основам і рівна їх півсумі:

m =	a + b
	2

4. Точка перетину діагоналей трапеції і середини основ лежать на одній прямій.

5. В трапеції бокову сторону видно із центра вписаного кола під кутом 90°.

6. Кожна діагональ в точці перетину ділиться на дві частини з таким співвідношенням довжини, як співвідношення між основами:

BC : AD = OC : AO = OB : DO

7. Діагоналі трапеції d₁ і d₂ пов'язані зі сторонами співвідношенням:

d₁² + d₂² = 2ab + c² + d²