Урок 45. Геометрія 7 клас "Рівнобедрений трикутник"
Здійснити діагностику засвоєння знань та вмінь з теми «Перша та друга ознаки рівності трикутників».
Домогтися свідомого розуміння учнями:
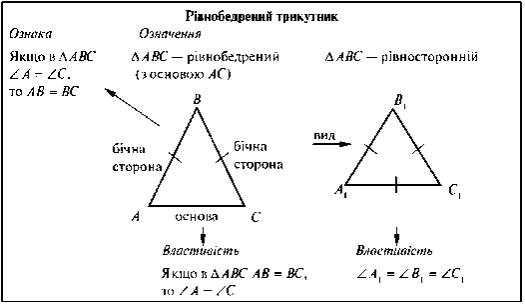
означення рівнобедреного трикутника, назви його елементів та властивостей і ознак;
означення рівностороннього трикутника та того факту, що рівносторонній трикутник можна вважати рівнобедреним.
Урок № 45
Геометрія 7 клас
Дата:
Тема уроку. Рівнобедрений трикутник
Мета уроку: здійснити діагностику засвоєння знань та вмінь з теми «Перша та друга ознаки рівності трикутників».
Домогтися свідомого розуміння учнями:
· означення рівнобедреного трикутника, назви його елементів та властивостей і ознак;
· означення рівностороннього трикутника та того факту, що рівносторонній трикутник можна вважати рівнобедреним.
Сформувати первинні вміння:
· використовуючи означення, розпізнавати на рисунку або за умовою рівнобедрений трикутник та називати його елементи;
· відтворювати властивості та ознаки рівнобедреного та рівностороннього трикутників та використовувати здобуті знання в процесі розв’язування задач.
Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця «Рівнобедрений трикутник», проектор, екран, презентація, комп’ютер.
ХІД УРОКУ
I. Організаційний етап
Перевірити готовність учнів до уроку, налаштування на роботу
II. Перевірка домашнього завдання
Самостійна робота
Варіант 1
Початковий рівень
1. У трикутниках ABC і KNM AB = KN, AC = KM, ![]() Доведіть, що ΔABC =ΔKNM.
Доведіть, що ΔABC =ΔKNM.
Середній рівень
2. У трикутниках ABC і BAD ![]() AD = 2 см. Знайдіть BC.
AD = 2 см. Знайдіть BC.
Достатній рівень
3. Відрізки AM і BN — відстані від точок A і B до прямої MN. Відомо, що AM = BN. Доведіть, що ![]()
Високий рівень
4. Відрізок AB є перпендикулярним до відрізка CD і проходить через його середину. Доведіть рівність трикутників ABC і ABD.
Варіант 2
Початковий рівень
1. У трикутниках ABC і XYZ ![]() , BC =YZ, AC = XZ. Доведіть, що ΔABC =ΔXYZ.
, BC =YZ, AC = XZ. Доведіть, що ΔABC =ΔXYZ.
Середній рівень
2. У трикутниках ABC і ABD ![]() BC = 8 см. Знайдіть BD.
BC = 8 см. Знайдіть BD.
Достатній рівень
3. Відрізки AM і BN — відстані від точок A і B до прямої MN. Відомо, що ![]() Доведіть, що AM = BN.
Доведіть, що AM = BN.
Високий рівень
4. Відрізок CD є перпендикулярним до відрізка AB і проходить через його середину. Доведіть рівність трикутників ACD і BCD.
III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку
Сьогоднішній урок пройде під девізом: «Те, що я встиг пізнати – чудово. Сподіваюся, таке ж чудове те, що мені ще доведеться пізнати»
Сократ
Оскільки трикутник та його види за сторонами й кутами розглядались у 5 класі, бажано звернутись до знань учнів та, активізувавши ці знання, сформулювати мету та завдання уроку.
IV. Актуалізація опорних знань
Вправа «Вільний мікрофон»
- Що називають трикутником?
- Які існують види трикутників за кутами? За сторонами??
- Який трикутник називається рівнобедреним?
- Як називають трикутник в якого всі сторони рівні?
- Як називаються сторони рівнобедреного трикутника?
- Сформулювати першу та другу ознаки рівності трикутників.
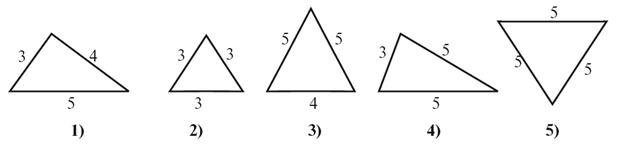
Серед трикутників зі вказаними довжинами сторін (рис. 1) виберіть один зайвий. Поясніть свій вибір.
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Означення рівнобедреного трикутника. Його елементи. Периметр рівнобедреного трикутника.
2°. Рівносторонній трикутник як особливий випадок рівнобедреного трикутника. Периметр рівностороннього трикутника.
3°. Теорема 1 про властивість кутів рівнобедреного трикутника та її доведення.
4°. Наслідок з теореми про кути рівнобедреного трикутника.
5. Теорема 2 – ознака рівнобедреного трикутника.
6. Наслідок з теореми 2.
VI. Первинне усвідомлення нового матеріалу
№ 323, 325, 327, 331 (усно)
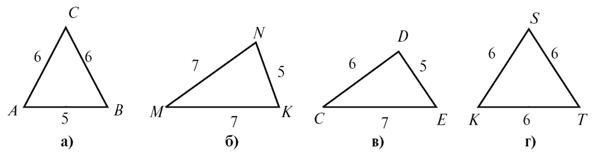
1. Які з трикутників, зображених на рисунку 2, є рівнобедреними? 2. Для рівнобедрених трикутників, зображених на рисунку 2, назвіть основи та бічні сторони. Обчисліть периметр кожного з рівнобедрених трикутників (найзручнішим способом).
3. Знайдіть периметр рівнобедреного трикутника, якщо:
а) бічна сторона дорівнює 6 см, а основа в 3 рази менша;
б) основа дорівнює a см, а бічна сторона на 2 см більша за основу.
4. У трикутнику DEF DE = EF. Назвіть рівні кути трикутника.
5. Трикутник ABC — рівнобедрений з основою AC, ![]() Чому дорівнює кут C?
Чому дорівнює кут C?
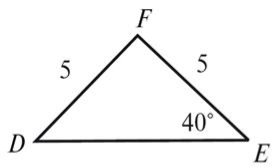
6. Чому дорівнює кут D трикутника DEF, зображеного на рисунку 3?
За підручником: № 329, 332.
![]()
Робота в групі
Рівень А
1. Периметр рівнобедреного трикутника дорівнює 2,6 м. Знайдіть сторони трикутника, якщо його основа більша від бічної сторони на 0,2 м.
2. Якщо бічна сторона й кут, протилежний основі одного рівнобедреного трикутника, відповідно дорівнюють бічній стороні й куту, протилежному основі, іншого рівнобедреного трикутника, то такі трикутники рівні. Доведіть.
Рівень Б
За підручником: № 329, 332.
Додатково
Периметр рівнобедреного трикутника дорівнює 21 м. Знайдіть сторони трикутника, якщо одна з них більша за іншу на 3 м. Скільки розв’язків має задача?
VII. Підсумок уроку
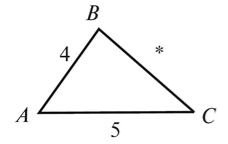
Яке число можна поставити замість *, щоб Δ ABC був рівнобедреним:
а) з основою AB; б) з основою AC? Для кожного випадку запишіть рівні кути (рис. 4).
Виконання тестової самостійної роботи в 2 варіантах.
I Варіант.
1. Якщо в рівнобедреному трикутнику ABC, AB=BC і ∠A=50°, то ∠C =
a) 100°; б) 80°; в) 50°; г) 40°.
2. Якщо основа рівнобедреного трикутника 5см, а бічна сторона 6см, то периметр трикутника:
а) 11см; б) 15см; в) 17см; г) 22см.
3. Якщо периметр рівнобедреного трикутника 27см, а його основа 7см, то бічна сторона трикутника:
а) 7см; б) 10см; в) 11см; г) 5см.
4. Якщо периметр рівнобедреного трикутника 35см, а його бічна сторона 13см, то основа дорівнює:
а) 13см; б) 15см; в) 9см; г) 10см.
5. Якщо дві сторони рівнобедреного трикутника дорівнюють 8см і 9см, то периметр дорівнює…
II Варіант.
1. Якщо в рівнобедреному трикутнику ABC AB=BC і ∠A=40°, то ∠C =
a) 100°; б) 80°; в) 50°; г) 40°.
2. Якщо основа рівнобедреного трикутника 8см, а бічна сторона 7см, то периметр трикутника:
а) 11см; б) 15см; в) 17см; г) 22см.
3. Якщо периметр рівнобедреного трикутника 27см, а його основа 5см, то бічна сторона трикутника:
а) 7см; б) 10см; в) 11см; г) 5см.
4. Якщо периметр рівнобедреного трикутника 35см, а його бічна сторона 10см, то основа дорівнює:
а) 13см; б) 15см; в) 9см; г) 10см.
5. Якщо дві сторони рівнобедреного трикутника дорівнюють 7см і 5см, то периметр дорівнює…
Правильні відповіді
I Варіант: 1.в) 50°; 2.в) 17см; 3.б) 10см; 4.в) 9см; 5. 25см або 26см.
II Варіант: 1.г) 40°; 2.г) 22см; 3.в) 11см; 4.б) 15см; 5. 19см або 17см.
VIII. Рефлексія
На сьогоднішньому уроці:
- повторили…
- з’ясували…
- розв’язали…
- дізналися…
- досягли…
Домашнє завдання
За підручником § 14 – опрацювати, №№ 330 (С), 341 (Д).


про публікацію авторської розробки
Додати розробку