Урок №5. Тиск газу. Рівняння стану ідеального газу

Мета: з'ясувати механізм тиску ідеального газу та його залежність від мікропараметрів.

Тип уроку: Комбінований урок.

Обладнання: комп’ютер, презнтація (електронний додаток ППЗ «Фізика 10. Основи МКТ»).

Демонстрації:

1. Модель тиску газу. 2. Фрагмент відеофільму «Молекули й молекулярний рух».

3. ОК-4.

План викладення нового матеріалу.

1.                        Основне рівняння МКТ ідеального газу.

2.                        Зв'язок тиску із середньою кінетичною енергією молекул МПЗ: математика, фізика 8, 10 клас.

План.

Етапи уроку	Методи й форми роботи з класом
I.          Організаційний       етап.   Перевірка домашнього завдання.	Якісні запитання. Фізичний диктант
II. Повідомлення теми, мети й завдань уроку; мотивація навчальної діяльності учнів.	Повідомлення нового матеріалу – презентація учителя, запис в зошити.
III. Застосування набутих знань.	Розв’язування задач.
IV. Підведення підсумків уроку та повідомлення домашнього завдання.	Коментар      учителя,        домашнє експериментальне завдання.

Фізичний диктант.

1в	2в	3в
1.Формула       молярної      маси через Мr М=Мr·10-3кг/моль	Кількість речовини через масу m і молярну масу   M	Кількість речовини число молекул і Авогадро   N A	через число
2.Концентрація        молекул N n V	Маса однієї молекули  m0 1,66 10 27 кг M r	число молекул в тілі m NN A M
3.Основне рівняння МКТ 1 p                  0              3	Середня кінетична енергія (зв'язок з абсолютною температурою) E k kT	Основне         рівняння         МКТ (зв'язок з температурою) р=nkT
4.Універсальна газова стала R=8,31Дж/моль·К	Число                             Авогадро NА=6,02·10231/моль	Стала Больцмана  k=1,38·10-23Дж/К
5.Температура – міра середньої кінетичної енергії.	Основні макроскопічні параметри,   що характеризують ідеальний газ: р, Т, V	Зв'язок температури t з абсолютною температурою: Т=t+273(К)
6.Молярна маса	Моль	Кількість речовини
7.Осмос	Дифузія	Броунівський рух

Викладання нового матеріалу.

. Основне рівняння МКТ.

Припущення: 1) газ ідеальний, тобто зіткненнями нехтуємо;

2)   швидкості молекул приблизно однакові;

3)   усі напрями у просторі (напрями руху молекул) рівноймовірні.

Дозволяє: знайти тиск газу р, якщо відомі маса молекули газу m0, середнє значення

2 квадрата швидкості молекул  та концентрація молекул n.

Виводиться за допомогою законів механіки.

В результаті кожного зіткнення між молекулами і молекул із стінками швидкості молекул можуть змінюватися по модулю і по напряму; на інтервалах часу між послідовними зіткненнями молекули рухаються рівномірно і прямолінійно. В моделі ідеального газу припускається, що всі зіткнення відбуваються по законах пружного удару, тобто підкоряються законам механіки Ньютона.

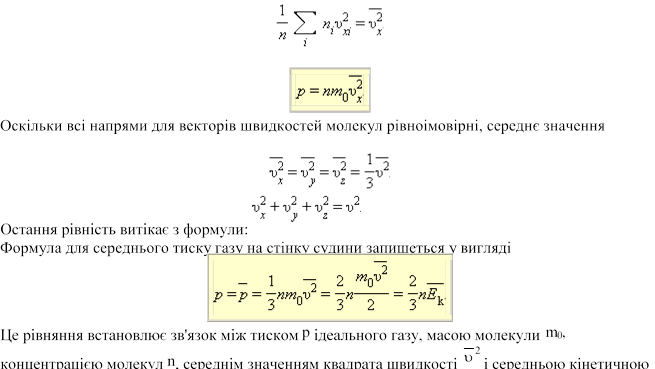
Використовуючи модель ідеального газу, обчислимо тиск газу на стінку посудина. В процесі взаємодії молекули із стінкою посудина між ними виникають сили, що підкоряються третьому закону Ньютона. В результаті проекція υ_х швидкості молекули, перпендикулярна стінці, змінює свій знак на протилежний, а проекція υ_y швидкості, паралельна стінці, залишається незмінною (рис.  15).

 

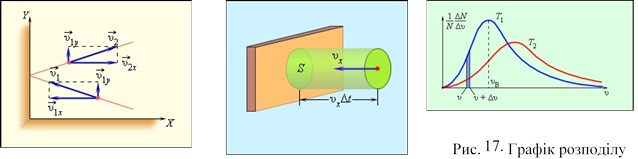
Рис. 15. Проекції швидкостей        Рис. 16. Визначення тиску молекул

Тому зміна імпульсу молекули буде рівна 2m₀υ_х, де m₀ – маса молекули.

Виділимо на стінці деякий площу S (рис. 16). За час Δt з цією площею зіткнуться всі молекули, що мають проекцію швидкості υ_х, направлену у бік стінки, і що знаходяться в циліндрі з підставою площі S і заввишки υ_хΔt.

Хай в одиниці об'єму посудини містяться n молекул; тоді число молекул в об'ємі циліндра рівно nSυ_хΔt. Але з цього числа лише половина рухається у бік стінки, а інша половина рухається в протилежному напрямі і із стінкою не стикається. Отже, число ударів молекул об площу S за час Δt дорівнює 

 

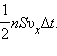
Оскільки кожна молекула при зіткненні із стінкою змінює свій імпульс на величину 2m₀υ_х, та повна зміна імпульсу всіх молекул, що зіткнулися за час Δt з площею S, дорівнює

 

За законами механіки ця зміна імпульсу всіх що зіткнулися із стінкою молекул відбувається під дією імпульсу сили FΔt, де F – деяка середня сила, діюча на молекули з боку стінки на площу S. Але по 3-му закону Ньютона така ж по модулю сила діє з боку молекул на площу S. Тому можна записати: 

 

Розділивши обидві частини на SΔt, отримаємо: 

 

де p – тиск газу на стінку судини.

При висновку цього співвідношення передбачалося, що всі n молекул, що містяться в одиниці об'єму газу, мають однакові проекції швидкостей на вісь Ох. Насправді це не так.

В результаті численних зіткнень молекул газу між собою і з стінками в судині, що містить велике число молекул, встановлюється деякий статистичний розподіл молекул по швидкостях. При цьому всі напрями векторів швидкостей молекул виявляються рівноправними (рівноімовірними), а модулі швидкостей і їх проекції на координатні осі підкоряються визначеним закономерностям. Розподіл молекул газу по модулю швидкостей називається розподілом Максвела, який у 1860 р. вивів закон розподілу молекул газу по швидкостях, виходячи з основних положень молекулярно-кінетичної теорії. На рис. 17 представлені типові криві розподілу молекул по швидкостях. По осі абсцис відкладений модуль швидкості, а по осі ординат – відносне число молекул, швидкості яких лежать в інтервалі від υ до υ +Δυ. Це число дорівнює площі виділеного на рис. 17 стовпчика.

Характерними параметрами розподілу Максвела є найвірогідніша швидкість υ_в, відповідна максимуму кривої розподілу, і середньоквадратична швидкість

 

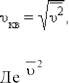– середнє значення квадрата швидкості.

Із зростанням температури максимум кривої розподілу зміщується у бік великих швидкостей, при цьому υ_в і υ_кв збільшуються.

 

 

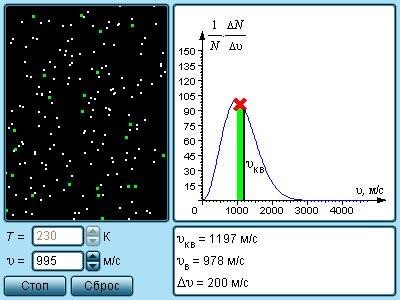
Модель. Розподіл Максвела

Щоб уточнити формулу для тиску газу на стінку судини, припустимо, що всі молекули, що містяться в одиниці об'єму, розбиті на групи, містить n₁, n₂, n₃ і т.  д. молекул з проекціями швидкостей υx1, υx2, υx3 і т.  д. відповідно. При цьому Кожна група молекул вносить свій внесок 

 

в тиск газу. В результаті зіткнень із стінкою молекул з різними значеннями проекцій υxi швидкостей виникає сумарний тиск 

 

Що входить в цей вираз сума – це сума квадратів проекцій υx всіх n молекул в одиничному

об'ємі газу. Якщо цю суму розділити на n, то ми отримаємо середнє значення квадрата проекції швидкості молекул: 

Тепер формулу для тиску газу можна записати у вигляді 

квадратів їх проекцій на координатні осі рівні між собою: 

 

енергією E k поступального руху молекул. Його називають основним рівнянням молекулярнокінетичної теорії газів.

Таким чином, тиск газу рівно двом третинам середньої кінетичної енергії поступального руху молекул, що містяться в одиниці об'єму.

‚. Зв'язок тиску із середньою кінетичною енергією молекул.

Якщо через E позначити середню кінетичну енергію поступального руху молекули E    ,

2

то ми можемо записати основне рівняння МКТ у вигляді p

                                                                                                                                              3          2

Отже, тиск ідеального газу пропорційний добуткові концентрації молекул на середню кінетичну енергію поступального руху молекули.

p        nkT

Наслідки основного рівняння МКТ: 1. р~nT, р=knT, або  , де k=1,38·10^-23Дж/К – стала Больцмана.

 

 

2. 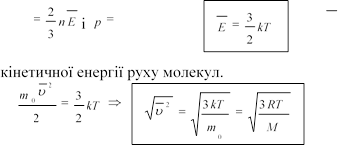                                                                                                                                                         p   nkT , отже                           , Т~ E , значить, температура є мірою середньої 

 

3.                                                                                                                                                          , де _{с.кв .} - середня квадратична швидкість, 

 

 

де R=8,31Дж/К·моль.

Запитання до учнів у ході викладання нового матеріалу.

1.Як обчислити зміну імпульсу молекули у разі удару її об стінку посудини?

2.Чому можна вважати, що молекули в газі рухаються лише уздовж трьох взаємно перпендикулярних напрямків?

3.Яким є механізм виникнення тиску газу з точки зору молекулярно – кінетичної теорії будови речовини?

Задачі, розв'язувані на уроці.

1.Кисень перебуває у н.у. Обчислити середню квадратичну швидкість молекул газу.

                                  

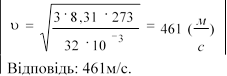
2.Визначити кінетичну енергію хаотичного поступального руху всіх молекул будьякого газу в балоні ємністю 5 л за тиску 1МПа. (7,5 кДж)

3.Чому дорівнює середня кінетична енергія хаотичного руху молекул аргону, якщо

2 кг його, перебуваючи у посудині об'ємом 2м³, чинять тиск 3·10⁵ Па? (6·10^-20 Дж)

Домашнє завдання: [1]§41.

ДОДАТКОВА ІНФОРМАЦІЯ

Дослід Штерна.

Вирішальними для доказу МКТ є досліди, у яких безпосередньо виявляються окремі молекули або атоми, а також вимірюються швидкості їхнього руху. Одним із перших експериментів, де були безпосередньо виміряні швидкості руху окремих молекул газу, був дослід О.Штерна, здійснений у 1920р. Здобуте з цього досліду значення середнього квадрата швидкості руху атомів Аргентуму виявилося в межах можливих похибок вимірювань, що збігаються зі значенням швидкості, здобутим теоретичним шляхом.

Збіг експериментально знайдених швидкостей руху молекул газу зі значеннями, що були передбачені МКТ, є одним із найважливіших прямих доказів справедливості МКТ газів.

Можна звернути увагу

Звертаю увагу учнів на одну важливу обставину. У досліді Штерна швидкість молекул визначалася за різних температур за рахунок зміни розжарення волоска, з якого відбувалося випарювання речовини. Виявилося, що у разі підвищення температури швидкість     молекул збільшується,           а          у          разі     зниження      –          зменшується.           Це експериментально підтверджує молекулярно – кінетичне визначення абсолютної температури.

Молекули срібла вилітають із розжареного стержня і через отвір у циліндрі А потрапляють на циліндр В. Якщо циліндри рухаються зі сталою кутовою швидкістю ω (частотою ν), то на циліндрі В утворюється смужка срібла, зміщена вбік від точки В на

відстань s. . Але t                                                   . Тоді 

t

T

Швидкість молекул газу (дослід Штерна, 1920)                                   

ω

 А  м

                                                               ^{B                                                         B}                                       500     

                   s                T                              s                                     s                        _с                              О

      Молекули срібла вилітають із розжареного стержня і через отвір

       у циліндрі А потрапляють на циліндр В.                                                                                                  s

В    Крива розподілу

                 

Максвелла

 

Середня швидкість теплового руху молекул.

             Рівняння E                        kT дає можливість знайти середній квадрат швидкості руху

молекули.               Підставляючи              до               цього               рівняння              формулу

 , дістанемо        :                               kT , звідки     :                          .

                   2                                              2

Обчислюючи за цією формулою швидкість молекул, наприклад азоту, при t=0ºС,

м дістанемо . Молекули водню за тієї ж температури мають середню швидкість

с 1800м/с.

Запитання до учнів у ході викладання нового матеріалу.

1.Як зміниться середня квадратична швидкість руху молекул у разі збільшення температури в 4 рази?

2.Які молекули в атмосфері рухаються швидше: азоту чи кисню?

Задачі, розв'язувані на уроці.

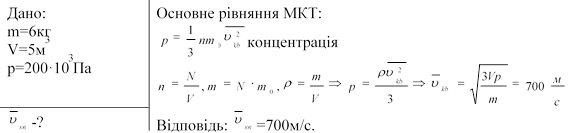
1.Чому дорівнює середня квадратична швидкість руху молекул газу, якщо він має масу 6кг, об'єм 5м³ при тиску 200кПа?

2.У скільки раз зміниться тиск одноатомного газу в результаті зменшення його об'єму в 3 рази і збільшення середньої кінетичної енергії його молекул в 2 рази?

2

                                                                            Основне рівняння МКТ в даному випадку p            nE

3

22

Дж .

 

Дж.

4.Знайти швидкість молекул срібла у досліді Штерна, якщо кутове зміщення їх дорівнює 5,4º при частоті обертання 150с^-1. Відстань між циліндрами 2см.

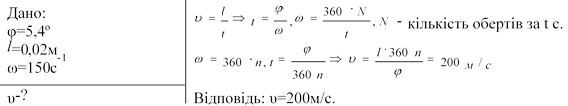
Список використаних джерел

1. Коршак Є. В. Фізика : 10 кл. : [підруч. для загальноосвіт. навч. закл. : рівень стандарту] / Є. В. Коршак, О. І. Ляшенко, В. Ф. Савченко. – К. : «Генеза», 2010. – 192 с. 2. Туманцова О. О. Фізика. 10 клас. Рівень стандарту: Розробки уроків /

О. О. Туманцова. – Х.: «Ранок», 2010. – 320 с.

3.        Уроки фізики у 10 класі. Молекулярна фізика і термодинаміка / Руденко А. В., упорядник. – Х.: Вид. група «Основа», 2010. –139 с. – (Б-ка журн. «Фізика в школах України». Вип. 11 (83)).

4.        Щербина Т. Чому? Цікаві питання з фізики.10 клас / Т. Щербина. – К. : Ред.

загальнопед. газ., 2003. – 128 с. – (Бібліотека «Шкільного світу»).

5.        «Открытая физика.2.6. Часть 1».