Урок №6. Газові закони. Ізопроцеси

Мета: вивести залежність між макроскопічними параметрами (р, V, Т), що характеризують стан газу. Встановити залежність між двома макропараметрами газу за незмінного третього.

Тип уроку: Комбінований урок.

Обладнання: комп’ютер, інтерактивна дошка, програмне забезпечення SMART Notebook, презнтація (електронний додаток ППЗ «Фізика 10. Основи МКТ»).

Демонстрації:

1.   Залежність між об'ємом, тиском і температурою газу.

2.   Залежність тиску від об'єму за сталої температури.

3.   Залежність об'єму газу від температури за сталого тиску.

4.   Залежність тиску газу від температури за сталого об'єму. План викладення нового матеріалу.

1.Рівняння стану. Універсальна газова стала. Рівняння Клапейрона.

2.  Ізопроцеси.

3.  Ізотермічний процес.

4.  Ізобарний процес.

5.Ізохорний процес.

МПЗ: математика, історія.

План.

Етапи уроку	Методи й форми роботи з класом
I.          Організаційний       етап.   Перевірка домашнього завдання.	Якісні запитання. Гра «Ребуси».
II. Повідомлення теми, мети й завдань уроку; мотивація навчальної діяльності учнів.	Повідомлення нового матеріалу – презентація учителя, запис в зошити.
III. Застосування набутих знань.	Розв’язування задач.
IV. Підведення підсумків уроку та повідомлення домашнього завдання.	Коментар      учителя,        домашнє експериментальне завдання.

 

Перевірка знань.

1.     Що називається ідеальним газом?

2.     Які макроскопічні параметри газу?

3.     Що таке температура як термодинамічний параметр? Гра «Ребуси»

Мета: розвивати пізнавальний інтерес, увагу, уміння аналізувати і узагальнювати, робити висновок.

Розгадати ребус – це означає «перевести» усе те, що він містить, в літери, скласти осмислене слово.

Під час гри йде активне оволодіння мовою, міркування вголос, внутрішньо регульоване сприйняття дозволяють формувати мимовільної уваги, що виникає під впливом внутрішньо поставлених завдань або роздумів.

Форма роботи: індивідуальна,  групова і фронтальна.

Відкрити SMART Notebook сторінку 2 (всього 28 сторінок).

  Після закінчення гри і  при закритті програми SMART Notebook і презентації зміни не зберігати!!!

SMART Notebook слайд 2 – початок гри.

 

	–                  А ви любите розгадувати ребуси? Хто з вас знає правила розгадування ребусів? (Повторюємо правила. Ці правила можна заздалегідь повторити  з учнями.) –                  Сьогодні у нас буде урок-гра. Ми розділимося на 2 команди. У кожній команді має бути відповідальний. Вчитель відкриває слайд 2 – «Табло» (рис. 18). Кожна команда вибирає собі назву (або команда «1», команда «2», вчитель друкує на «Табло». Якщо команда розгадала ребус, їй додається очко. Якщо члени команди порушують правила гри або дисципліну, у них на «Табло» забираємо 1 бал. За посиланням у верхньому правому кутку «зірочка» переходимо в перший тур, після 12 розгаданих ребусів, переходимо за посиланням «ідея» в другий тур, що теж складається з 12 ребусів (використовуємо «барабан»).
Рис. 19. Слайд 3	Спочатку представники команд тягнуть жереб – хто перший розгадуватиме ребус. Потім представник «першої» команди натискає на «Барабан», він вкаже номер ребусу. Натискаємо обраний номер. Наприклад, сектор 4. Натискаємо на кульку з цифрою 4. Він відкриває посилання (рис. 19).
Рис. 20. Слайд 7.	Відповідь: ТЕМПЕРАТУРА. Тепер натискаємо кнопку повернення у верхньому лівому кутку «смайлик» (рис. 20).
Рис. 21. Результати гри	Якщо команда розгадала правильно, то їй на «Табло» додають 1 бал, краще, якщо це робитимуть самі діти. Потім за посиланням «зірочка» переходимо на слайд 3 – «Барабан». Аналогічно виконуємо розгадування інших ребусів (рис. 21)
Рис. 22. Барабан для другого туру гри	Після виконання завдань першого туру переходимо у другий (слайд №16). Для продовження, натискаємо на барабан. У нашому випадку стрілка зупинилася в секторі 15. Натискаємо кульку з цифрою 15, Натискаємо на кулькупосилання, переходимо до Ребусу № 15 (рис. 22, 23).	Рис. 23. Ребус №15

Та ж гра, але за допомогою презентації з макросами (рис. 24).

 

 

 

Рис. 24. Гра «Ребуси» проводиться за допомогою презентації

 

Допустимі     варіанти     введення    правильних     відповідей,    наприклад      «МАРІОТТ»,

«Маріотт», «маріотт»

Викладання нового матеріалу.

. Рівняння стану. Універсальна газова стала. Рівняння Клапейрона. Співвідношення p  =  nkT

пов'язує тиск газу із його температурою і концентрацією молекул, отримано  для моделі ідеального газу, молекули якого взаємодіють між собою і із стінками посудини лише під час пружних зіткнень. Це співвідношення може бути записано в іншій формі, що встановлює зв'язок між макроскопічними параметрами газу – об'ємом V, тиском p, температурою T і кількістю речовини ν. Для цього потрібно використовувати рівність 

 

Тут N – число молекул в посудині, N_А – постійна Авогадро, m – маса газу в посудина, M – мольна маса газу. У результаті отримаємо: 

 

Добуток постійної Авогадро N_А на k називається універсальною газовою постійною і позначається буквою R. Її чисельне значення в СІ є: 

R  =  8,31  Дж/моль·К. Співвідношення 

(1) 

 

називається рівнянням стану ідеального газу.

Для одного моля будь-якого газу це співвідношення приймає вигляд: 

Якщо температура газу рівна Tн =273,15К(0 °С), а тиск p_н =1атм = 1,013·10⁵Па, то говорять, що газ перебуває за нормальних умов. Як випливає з рівняння стану ідеального газу, один моль будь-якого газу за нормальних умов займає один і той же об'єм V₀, рівний 

V₀=0,0224м³/моль=22,4дм³/моль.

Це твердження називається законом Авогадро.

Для суміші невзаємодіючих газів рівняння стану приймає вигляд 

 де ν₁, ν₂, ν₃ і т. д. – кількість речовини кожного з газів в суміші.

Рівняння, що встановлює зв'язок між тиском, об'ємом і температурою газу було отримане в середині XIX  століття французьким фізиком Б. Клапейроном, у формі (1) воно було уперше записано Д.І.Менделєєвим. Тому рівняння стану газу називається рівнянням Клапейрона–Менделєєва.

Слід відзначити, що задовго до того, як рівняння стану ідеального газу було теоретично отримано на основі молекулярно-кінетичної моделі, закономірності поведінки газів в різних умовах були добре вивчені експериментально. Тому рівняння (1) можна розглядати як узагальнення дослідних фактів, які знаходять пояснення в молекулярно-кінетичній теорії.

Газ може брати участь в різних теплових процесах, при яких можуть змінюватися всі параметри, що описують його стан (p, V і T). Якщо процес протікає досить повільно, то у будь-який момент система близька до свого рівноважного стану. Такі процеси називаються квазістатичними. В звичному для нас масштабі часу ці процеси можуть протікати і не дуже повільно. Наприклад, розрідження і стискування газу в звуковій хвилі, що відбуваються сотні раз в секунду, можна розглядати як квазістатичний процес. Квазістатичні процеси можуть бути зображений на діаграмі станів (наприклад, в координатах p,  V) у вигляді деякої траєкторії, кожна точка якої представляє рівноважний стан.

‚. Ізопроцеси.

Інтерес представляють процеси, в яких один з параметрів (p, V або T) залишається незмінним. Такі процеси називаються ізопроцесами.

ƒ.Ізотермічний процес (T= const)

Ізотермічним процесом називають квазістатичний процес, що протікає при постійній температурі T. ІЗ рівняння (1) стану ідеального газу виходить, що при постійній температурі T і незмінній кількості речовини ν в посудині добуток тиску p газу на його об'єм V повинен залишатися постійним:  pV  =  const (рис. 25). 

 

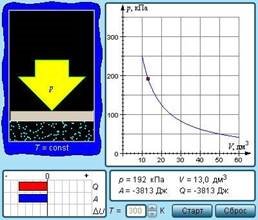
Рис. 25. Модель. Ізотермічний процес

На площині (p,  V) ізотермічні процеси зображаються при різних значеннях температури T сімейством гіпербол p~1/V, які називаються ізотермами. Оскільки коефіцієнт пропорційності в цьому співвідношенні збільшується із зростанням температури, ізотерми, відповідні більш високим значенням температури, розташовуються на графіку вище за ізотерми, відповідні меншим значенням температури (рис. 26). Рівняння ізотермічного процесу було отримано із експерименту англійським фізиком Р. Бойлем (1662 р.) і незалежно французьким фізиком Е. Маріоттом (1676 р.). Тому це рівняння називають законом Бойля–Маріотта.

 

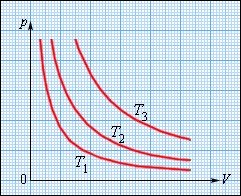
Рис. 26. Сімейство ізотерм на площині (p,  V). T₃ >T₂>T₁

„. Ізохорний процес (V = const) 

Ізохорний процес (рис. 27) – це процес квазістатичного нагрівання або охолоджування газу при постійному об'ємі V і за умови, що кількість речовини н в посудина залишається незмінною.

Як випливає з рівняння (1) стану ідеального газу, за цих умов тиск газу p збільшується прямо пропорційно його абсолютній температурі: p ~ T або 

 

 

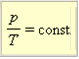
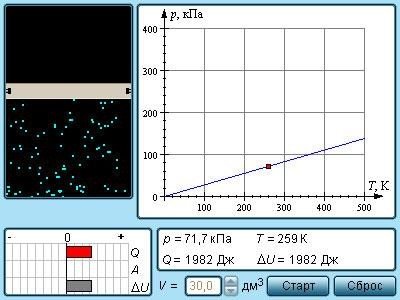
Рис. 27. Модель. Ізохорний процес На площині (p, T) ізохорні процеси для заданої кількості речовини н при різних значеннях об'єму V змальовується сімейством прямих ліній, які називаються ізохорами. Великим значенням об'єму відповідають ізохори із меншим нахилом по відношенню до осі температур (рис.  28).

 

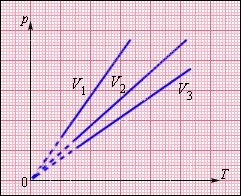
Рис. 28. Сімейство ізохор на площині (p,  T). V₃ >V₂ >V₁

Експериментально залежність тиску газу від температури досліджував французький фізик Ж. Шарль (1787 р.). Тому рівняння ізохорного процесу називається законом Шарля. Рівняння ізохорного процесу може бути записано у вигляді: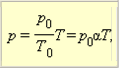   

 де p₀ – тиск газу при T =T₀=273,15К (тобто при температурі 0°С). Коефіцієнт α, рівний (1/273,15) К^–1, називають температурним коефіцієнтом тиску.

…. Ізобарний процес (p= const) (рис. 29)

Ізобарним процесом називають квазістатичний процес, що протікає при незмінному тиску p.

Рівняння ізобарного процесу для деякої незмінної кількості речовини ν має вигляд: 

де V₀ – об'єм газу при температурі 0°С. Коефіцієнт α рівний (1/273,15)К ^–1. Його називають температурним коефіцієнтом об'ємного розширення газів.

 

 

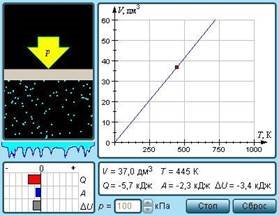
Рис. 29. Модель. Ізобарний процес На площині (V, T) ізобарні процеси при різних значеннях тиску p зображаються сімейством прямих ліній (рис. 30), які називаються ізобарами.

 

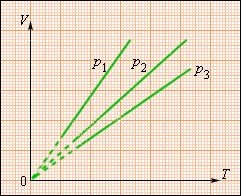
Рис. 30. Сімейство ізобар на площині (V,  T). p₃>p₂ >p₁

Залежність об'єму газу від температури при незмінному тиску була експериментально досліджена французьким фізиком Гей-Люссаком (1862 р.). Тому рівняння ізобарного процесу називають законом Гей-Люссака.

Експериментально встановлені закони Бойля–Мариотта, Шарля і Гей-Люссака знаходять пояснення в молекулярно-кінетичній теорії газів. Вони є слідством рівняння стану ідеального газу.

Запитання до учнів у ході викладання нового матеріалу.

1.Що ви розумієте під параметрами тану?

2.Які параметри характеризують стан газу?

3.Яка форма рівняння стану містить більше інформації: рівняння Клапейрона або Менделєєва – Клапейрона?

4.Зобразіть графік ізотермічного процесу в координатах (V, Т) і (р,Т).

5. Зобразіть графік ізобарного процесу в координатах (р, Т) і (р, V). 6. Зобразіть графік ізохорного процесу в координатах (V, Т) і (р,V).

 

Задачі, розв'язувані на уроці.

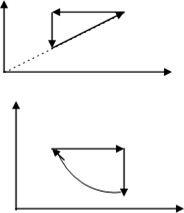
1.Як змінювалась температура ідеального газу при процесі, графік якого в координатах р –V на малюнку 31,а?

        р р                 Т_max                                                Накресливши        сімейство         гіпербол,

  знаходимо відповідь

  

              Т_min

         0                  V 0        V Рис. 31,а    Рис. 31,б

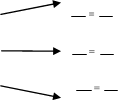
2.Стан деякого газу сталої маси змінюється за графіком:

-         назвати процеси;

-         написати рівняння процесів;

-         побудувати графіки процесів в координатах (р, V)

V         2                  1                                                                                     3 0                                    Т                р                            3               1                                                   2 0                                       V

p         p 1-2 – V=const, Т↓, , р↓;                                               T1             T2 2-3 – Т= const, рV= const, V↓, р↑; V 3-1 – р= const,       const , Т↑, V↑ T

До конспекту учня

Об'єднаний закон стану газу pV RT рівняння Менделєєва – Клапейрона			p, V, T – параметри стану газу, R=8,31 R – універсальна газова стала
Ізопроцеси – процеси, при яких одна з фізичних величин залишається сталою. Газові ізопроцеси m                                                                     Т=const                      p2          V1         Закон Бойля – Маріотта                                                                                                                  p1        V2                 р=const                      V2          T2         Закон Гей-Люссака                                                                                                                 V1          T1                µ                 V=const                     p2             T2            p1                                     T1                                        Закон Шарля Т=t+273
Нормальні умови р=р0, Т=Т0			Т0 – температура плавлення льоду, Т0=273К
Ізотермічний процес, Т=const, рV=const     р               Т2>Т1              Т2    Т1      0                V	Ізобарний процес, р=const,   V              T V1            T1 V=V0αT, α=1/Т0    V    р1 р2   0                           р2>р1             Т	Ізохорний процес  V=const, р=р0αТ             p          T   р           V1                       p1              T1 V2                                             V2>V1 0 Т

Домашнє завдання: [1]§42, 43, 45,46

Список використаних джерел

1. Коршак Є. В. Фізика : 10 кл. : [підруч. для загальноосвіт. навч. закл. : рівень стандарту] / Є. В. Коршак, О. І. Ляшенко, В. Ф. Савченко. – К. : «Генеза», 2010. – 192 с. 2. Туманцова О. О. Фізика. 10 клас. Рівень стандарту: Розробки уроків /

О. О. Туманцова. – Х.: «Ранок», 2010. – 320 с.

3.        Уроки фізики у 10 класі. Молекулярна фізика і термодинаміка / Руденко А. В., упорядник. – Х.: Вид. група «Основа», 2010. –139 с. – (Б-ка журн. «Фізика в школах України». Вип. 11 (83)).

4.        Щербина Т. Чому? Цікаві питання з фізики.10 клас / Т. Щербина. – К. : Ред.

загальнопед. газ., 2003. – 128 с. – (Бібліотека «Шкільного світу»).

5.        «Открытая физика.2.6. Часть 1».