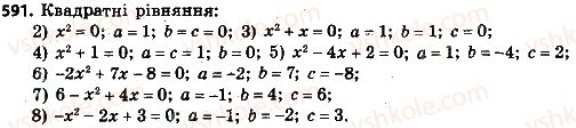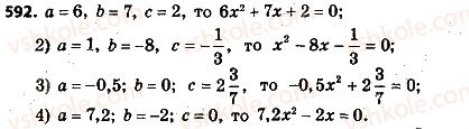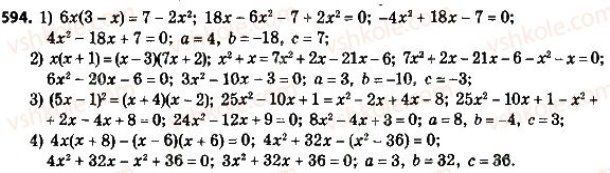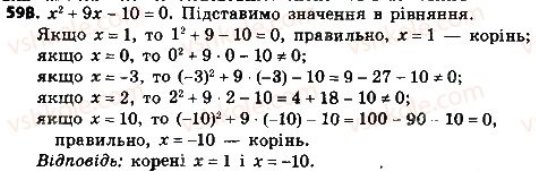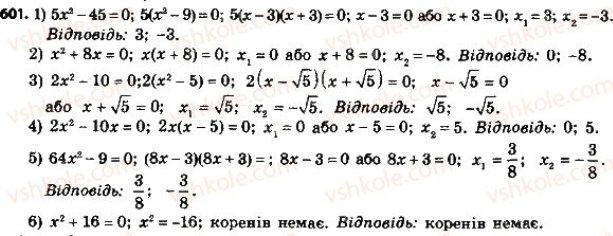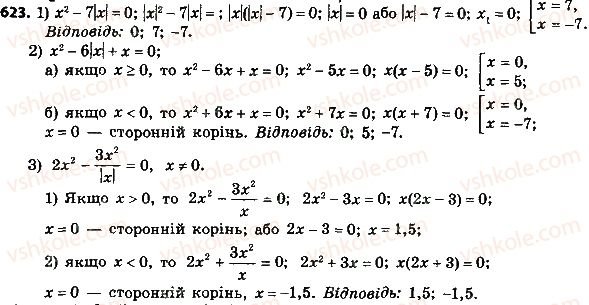Урок алгебри 8 клас. "Квадратні рівняння. Неповні квадратні рівняння"

Урок №

Алгебра 8 клас

Дата: 

Тема уроку: Квадратні рівняння. Неповні квадратні рівняння

Математичні здібності визначаються двома основними рисами: умінням мислити логічно і умінням мислити нешаблонно.

В.І.Шевченко

Мета уроку:

Навчальна:

  сформувати поняття про квадратне рівняння, неповне квадратне рівняння, види неповних квадратних рівнянь та способи їх розв`язання;

  сформувати уміння розпізнавати неповні квадратні рівняння, визначати їх коефіцієнти, розкладати на множники, розв`язувати неповні квадратні рівняння;

  продовжити роботу над розвитком умінь порівнювати, аналізувати робити висновки; удосконалювати навички само та взаємоконтролю.

 Розвивальна: розвивати абстрактне та логічне мислення, математичну мову, роботу в групах, парі.

Виховна: виховувати наполегливість у здобутті знань, толерантність, вміння спілкуватися.

Тип уроку: урок вивчення нового матеріалу 

Хід уроку

І. Організаційний етап

Перевірити готовність учнів до уроку, налаштувати учнів на плідну працю

ІІ. Актуалізація опорних знань

Вправа «Мікрофон»

• Що таке рівняння?
• Що означає розв’язати рівняння?
• Що таке розв’язок (корінь) рівняння?
• Чи є число 3 розв’язком рівняння х + 5 = 7? 4х = 12?
• Які рівняння ви вмієте розв’язувати і як їх називають?
• Які рівняння називають лінійними з однією змінною?
• Які рівняння називають рівносильними?
• Чи рівносильні рівняння: 3х – 6 = 9 і -2х = -10?
• Які властивості мають рівносильні рівняння?
• Як розв’язати рівняння виду: 2х = 64;      х² = 16;     2х²= 20;     21х²- х = 0?  
• Які це дробово – раціональні рівняння?
• Як розв’язати рівняння: = 0?
• Як розв’язати рівняння виду: 2х = 64;      х² = 16;     2х²= 20;     

21х²- х = 0? 

   2. Мотивація навчальної діяльності

Сьогодні на уроці мова піде про рівняння виду;      х² = 16;     2х²= 20; х² + 5х – 3 = 0. Такі рівняння називають квадратними. Ми з вами піднімаємося ще на одну сходинку вище у знаннях про рівняння.  Як сказав відомий американський математик Джордж Пойа  ви повинні зрозуміти, яке важливе значення мають квадратні рівняння. Простіші види вавилонські математики вміли розв’язувати ще 4 тис. років тому. Згодом розв’язували їх також в Китаї і Греції.

ІІІ. Вивчення нового матеріалу

    План вивчення нового матеріалу:

1. Означення квадратного рівняння. Коефіцієнти квадратного рівняння.

2. Зведене квадратне рівняння.

3. Неповне квадратне рівняння. Види неповних квадратних рівнянь.

Складіть рівняння до задачі.

Задача. Ділянку землі прямокутної форми, яка має площу 875 кв. м і прилягає до стіни, треба відгородити металевою сіткою, довжина якої 85 м. Якими будуть довжина і ширина ділянки?

Учні класу працюють в парах. Складене рівняння перевіряється учнями за заздалегідь заготовленими записами. Нехай х м – ширина ділянки. Тоді її довжина буде (85 – 2х) м. Площа ділянки за умовою дорівнює 875 кв. м. Складемо рівняння: х(85 – 2х) = 875. Розкриваючи дужки, переносячи 875 у ліву частину рівності і змінюючи знак рівності на протилежний, дістанемо: 2х²– 85х + 875 = 0. Ліва частина даного рівняння є многочлен другого степеня з однією змінною, а права – нуль.

Таке рівняння ми поки що розв’язати не можемо, це новий для вас тип рівнянь, що називаються квадратними.

Квадратичним рівнянням називається рівняння виду де змінна,       а,b, c – деякі числа, причому

Наприклад:  -х² + 6х + 5 = 0;  8х² – 7 = 0;  2х² + 4 = 0 ; х² – 4 = 0;  х² = 5 – квадратичні рівняння.

Числа а, b, c – коефіцієнти квадратного рівняння. Число а називають першим коефіцієнтом,  b – другим, с – вільним членом.

Квадратне рівняння називають ще рівнянням другого степеня, оскільки його ліва частина є многочлен другого степеня.

Рівняння, в яких перший коефіцієнт а = 1, такі квадратні рівняння називають зведеними квадратними рівняннями.

    ←  повне квадратне рівняння

          ← зведене квадратне рівняння

Приклади зведених квадратних рівнянь:

Якщо в квадратному рівнянні хоча б один з коефіцієнтів b або с дорівнює нулю, то таке рівняння називають неповним квадратним рівнянням.

Так рівняння: - 2х² + 7 = 0;  3х² – 10х = 0;  4х² = 0 – неповні квадратні рівняння.

У першому з них: b = 0; у другому – с = 0; у третьому b = 0 і с = 0.

Неповні квадратні рівняння

(бувають трьох видів, )

① ах² + с = 0, де с b = 0                                                                          ③ах² = 0, де b = 0, с = 0

②ах² + bх = 0, де b, с = 0

Розглянемо розв’язування рівнянь кожного з цих видів:

①.   - 3х² + 15 = 0,

         - 3х² = - 15                                   ах² + с = 0, де с 

             х² = 5                                        ах² = - с

          х₁ = або х₂ = -                 х² = т.к. с , тоді -.

Якщо х² =, тоді рівняння має два кореня: х₁ = ; х₂ = -  

Якщо тоді рівняння ах² + с = 0 немає коренів.

②.   4х² + 9х = 0

          х²(4х + 9) = 0

          х = 0 або 4х + 9 = 0                    ах² + bх = 0, де b

          х₁ = 0 , х₂ = -                            х(ах + b) = 0,  х₁= 0 або ах + b = 0, х₂ = -

Таким чином, неповне квадратне рівняння виду ах² + bх = 0 при b завжди має два корені (один з яких  буде завжди х = 0).

③.  5х² = 0,  5   Неповне квадратне рівняння ах² =0 рівносильне

          х² = 0 і тому має єдиний корінь х = 0.

IV. Формування вмінь

1. Робота за підручником А.Г. Мерзляк

Розв’язати усно 2. Розв’язування вправ

Робота в групі

              Колективно, коментовано:

              Самостійна робота навчального характеру:

           Розв’язати рівняння:

          Розв’язання. 

 рівняння не має                     розв’язків.

V. Підсумки уроку. Рефлексія

• Що нового ви дізналися на уроці?
• Чи зрозумілим був матеріал?
• Над чим потрібно попрацювати вдома?

VІ. Домашнє завдання

Опрацювати §3, п. 18, № 593, 602 (с.р.); № 604 (д.р.); 623 (в.р.)