Урок "Алгоритми з розгалуженням при розв’язуванні квадратних рівнянь"

Тема:  Алгоритми з розгалуженням при розв’язуванні квадратних рівнянь

Клас: 8 клас.

Мета:

1. Розкрити таємниці та причини виникнення квадратних рівнянь, історію виникнення формул для розв’язування квадратних рівнянь. Розвивати уміння програмувати та розв’язувати квадратні рівняння.
2. Розвивати позитивне мислення, критичне мислення, уміння аналізувати інформацію, самостійність, адаптивність, уміння концентруватись, кмітливість, логічне мислення, пам’ять.
3. Виховувати персональну відповідальність, інформаційну культуру учнів, культуру мови.

Опис ситуації:

Ми так часто чуємо  «рівняння» - математичний опис життєвої ситуації, але яка ситуація була першою, що дала поштовх виникненню рівнянь.

Питання кейсу:

1. Які ж рівняння називаються квадратними та коли вони виникли?
2. Хто винайшов формули для знаходження квадратних рівнянь?
3. Які практичні знання мені знадобляться?
4. Чи можливо створити програму для розв’язування квадратних рівнянь?

Три розгортки з предметів.

Історія

Коли з’явилися перші квадратні рівняння? Які вони були?Які задачі призвели до їх винекнення?

Алгебра виникла у зв’язку з вирішенням різноманітних задач за допомогою рівнянь. Необхідність розв’язувати рівняння не тільки першого, а й другого порядку виникла в зв’язку з потребою вирішувати питання, пов’язані з земельними ділянками, з розвитком астрономії.

Згадки про квадратні рівняння можна знайти у єгипетських папірусах датованих приблизно 2000 р. до н.е.

 

 

 

 

Даний папірус знаходиться у Берлінському музеї і в ньому зустрічається наступна задача: «Квадрат та інший квадрат, сторона якого є ½+¼ сторони першого квадрата, мають разом площу 100. Обчисли мені це».

Цю задачу можна розв’язати склавши рівняння х²+ (½+¼)²х² = 100.

Вавилоняни вміли розв’язувати квадратні рівняння більше ніж 4000 р. тому. В ті часи царем Вавилону був великий Хаммураті. Правило розв’язків майже співпадає з сучасним, але невідомо, яким чином вавилоняни дійшли до цього. В клинописних текстах відсутні згадування про від’ємні числа та загальний метод розв’язування квадратних рівнянь.

 

Ось одна з вавилонських задач: «Площа А, яка складається з суми двох квадратів, складає 1000, сторона одного з квадратів складає 2/3 сторони іншого, зменшені на 10. Які сторони квадратів?»

(2/3х – 10)² + х² =1000.

В книзі записано простий хід розв’язування: «Піднеси до квадрату 10, це дає 100, відніми 100 від 1000, це дає 900…» і т.д.

 

 

 

 

 

 

 

Математики Стародавньої Греції використовували для розв’язування  лінійних і квадратних рівнянь метод прикладання площин. Прикладами таких задач є відшукання сторін правильних вписаних многокутників, яке називають «золотим перетином» відрізка, подання ребра правильного многокутника через діаметр описаної кулі і т.д.

Метод розв’язку залежав від квадратного рівняння. Такі методи давали лише один додатній корінь. Стародавні математики розуміли необхідність так формулювати умову задач, щоб вони заздалегідь мали додатні розв’язки.

 

 

 

 

 

 

 

У Стародавньому Китаї відомості про квадратні рівняння починають зустрічатись приблизно в ІІІ ст. до н.е.

Розглянемо приклад з трактату «Математика в дев’яти книгах» (ІІ ст. до н.е.): «Маємо місто з межею у вигляді квадратів зі стороною невідомої величини, в центрі кожної сторони знаходяться ворота, на відстані 20 бу ( 1 бу = 1,6м) від північних воріт (за межами міста) стоїть стовп, якщо пройти від південних воріт 14 бу прямо, потім повернути на захід і пройти ще 1775 бу, то  можна побачити стовп. Яка межа міста?»

Розв’язком цієї задачі є відповідь 250 бу. І знову ж таки китайські вчені від’ємний варіант розв’язку рівнянь не розглядають.

Задачі на квадратні рівняння зустрічаються в астрономічних трактатах «Аріабхатія», у 492 р. індійським математиком і астрономом Аріабхатою. Інший індійський вчений Брахмагупта ( VII ст.) виклав загальне правило розв’язування квадратних рівнянь.

А ось одна з задач відомого індійського математика ХІІ ст. Бхаскари: «Розділившись на дві зграї забавлялись мавпи в гаї. Одна восьма їх в квадраті танцювали вельми раді. А дванадцять на древах підняли веселий регіт, що навколо аж гуло. Скільки їх всього було?»

І саме в розв’язанні Бхаскари помічаємо, що він знаходить два корені рівняння, отже він знав про двояку властивість кореня.

 

 

 

 

 

 

 

 

 

 

Середньоазіатський вчений аль-Хорезмі (ІХст.) в трактаті “Китаб альджерб валь-мукабала” отримав формулу коренів квадратного рівняння методом виділення повного квадрата за допомогою геометричної ілюстрації.

Завдання:

 Відчуйте себе жителем стародавньої Індії та розв’яжіть задачу Бхаскари, обміняйтесь думками з однокласниками щодо розв’язання даної задачі.

Математика

Але хто ж знайшов формулу коренів квадратного рівняння? Та як її застосовують при розв’язування рівнянь?

 Загальне правило розв’язування квадратних рівнянь було сформоване німецьким математиком М. Штифелем (1487 — 1567). Виведенням формули загального розв’язку квадратних рівнянь займався Франсуа Вієт. Він же й вивів формули залежності коренів рівняння від коефіцієнтів у 1591 році. Після праць нідерландського математика А. Жирара (1595 — 1632), а також Декарта і Ньютона спосіб розв'язування квадратних рівнянь набув сучасного вигляду.

 Перегляньте схему розв’язування квадратних рівнянь та сучасну формулу знаходження коренів.

 

 

 

 

 

Завдання:

 Розв’яжіть квадратні рівняння:

1. 
2. 
3. .

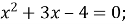
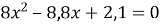Продемонструйте розв’язання однокласниками та вчителю.

 

Інформатика

Як скласти програму для розв’язання квадратних рівнянь за допомогою формули дискримінанту та чи необхідна  взагалі дана програма?

 Ви щойно розв’язали доволі прості квадратні рівняння. А що буде у випадку, коли коефіцієнти квадратного рівняння будуть або дуже великими, або дуже маленькими?

 В таких випадках не замінимою буде відповідна комп’ютерна програма.

 Розглянемо блок-схему такої програми.

 

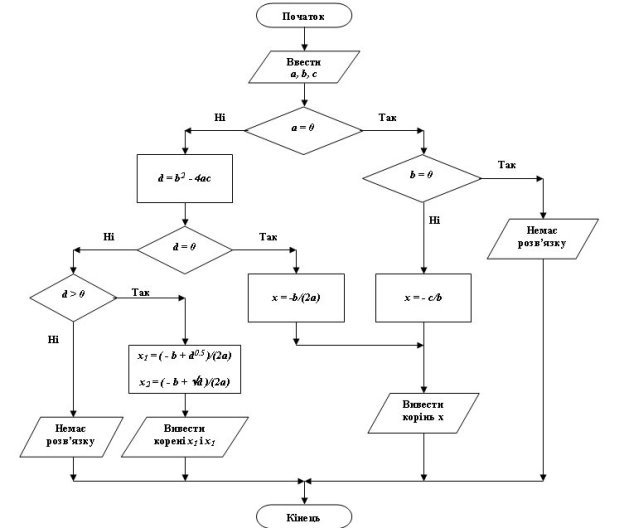
Завдання:

 Створіть програму, яка реалізуватиме дану блок-схему, тобто розв’язуватиме квадратні рівняння за допомогою формули дискримінанту.

 Перевірте дану програму за допомогою рівнянь, які ви вже розв’язали.

Підведення підсумків кейс-уроку

 

Список використаної літератури

1. Вікіпедія/[Електронний ресурс]/ https://uk.wikipedia.org/wiki.
2. Желізняк Л.Д. Кейс-технологія. Збірка кейсів з інформатики/ Л.Д. Желізняк// Інформатика в школі. – 2013. – №4. – С. 5 – 10.
3. Михайлова О. А. Кейс та кейс-метод /М.: «Центр», 1999. – 254 с.