Урок-бенефіс одного рівняння: "Розв’язування тригонометричних рівнянь"
Тема: Розв’язування тригонометричних рівнянь
Мета:Розвивати вміння розв’язувати тригонометричні рівняння різними способами,знаходити різні підходи до розв’язання поставлених завдань; розвивати самостійність , творчість та інтелект учнів ,логічне мислення , вміння робити висновки та узагальнення. Виховувати пізнавальні інтереси. Розширювати кругозір учнів. Здійснювати міжпредметні зв’язки.
Обладнання: картки, таблиці, ілюстрація, музика із кінофільму «Титанік», словник іншомовних слів.
Тип уроку: урок систематизації та узагальнення.
Форма проведення: урок – бенефіс.
Хід уроку
І. Організаційний момент
 ІІ. Мотивація пізнавальної діяльності учнів. Повідомлення теми, мети та завдань уроку.
ІІ. Мотивація пізнавальної діяльності учнів. Повідомлення теми, мети та завдань уроку.
(Ілюстрація) Як вигадаєте чому на дошці зараз з’явився індус із луком?
( Варіанти думок учнів).
Справа в тому, що перші тригонометричні тотожності були доведені математиками Індії, тоді відкриття індійців перешли до арабів. І перша функція, яку розглядали, була функція «синус». Це слово в перекладі з арабської мови, означає «тетева», бо власне індуси розглядали функцію синус як відношення півхорди до радіуса, що нагадує тетева лука. Особливо великі вимоги до розв’язування тригонометричних рівнянь ставили астрономи, бо людей цікавило питання як звідати невідоме в космосі, виміряти відстань до невідомої планети, передбачити сонячне затемнення. Перші тригонометричні таблиці склав Клавдій Птолемей, пізніше їх удосконалив російський вчений Леонтій Магніцький, а сучасного вигляду набула тригонометрія завдяки швейцарському математику, члену Петербурзької академії наук Леонарду Ейлеру. Будучи кореспондентом тієї ж академії наук наш земляк, уродженець хутора Пашеного Козельщанського повіту Полтавської губернії М. В. Остроградський створив підручник по тригонометрії для студентів технічних вузів.
Змістовні лінії математики мають свою структуру: спочатку вивчаються вирази, потім відповідні функції, рівняння, нерівності та їх системи.
Рівняння – це не просто рівність
З одною змінною чи кількома .
Рівняння – це думок активність ,
Це інтелекту боротьба.
Тож будьте творчими, активно розвивайтесь
Долайте труднощі у своєму житті,
Але з рівняннями, прошу не розлучайтесь
Вони послужать вам ще в майбутті.
Відомий англійський фізик та математик Альберт Ейнштейн говорив:
Мені постійно доводиться ділити свій час між рівняннями і політикою, але перевагу я віддаю рівнянням, так як політика змінна, а рівняння вічні.
Якою б професією ви в майбутньому не володіли, але вміти знаходити вихід із ситуацій, часто нетрадиційний – запорука вашої успішної роботи. Математика, як ніякий інший навчальний предмет, вчить варіативності мислення, вмінню творчо підходити до поставлених задач. Той, хто володіє таким творчим мисленням, безумовно - творча людина. «Що знаєте – не забувайте, чого не вмієте – навчайтесь», - так говорив Володимир Мономах. Ваше завдання – мобілізувати свої знання з алгебри, проявити творчий підхід до розв’язання рівняння, відшукати максимально можливу кількість способів їх розв’язання .
Тому на сьогоднішньому уроці ми поглинемо в світ тригонометричних рівнянь. Але форма проведення уроку буде незвична. Це буде урок – бенефіс. А взагалі що таке бенефіс?
«Бенефіс» - спектакль, який влаштовують на честь одного з акторів , що працюють в театрі.
Актором нашого дійства сьогодні буде тригонометричне рівняння :![]() . І наше завдання полягатиме в тому, щоб показати варіативність способів його розв’язання. Адже вміння розв’язувати рівняння – це вміння розв’язувати математичні моделі реального світу, якими вони виступають, це вміння знаходити вихід із ситуацій, які нам ставить життя.
. І наше завдання полягатиме в тому, щоб показати варіативність способів його розв’язання. Адже вміння розв’язувати рівняння – це вміння розв’язувати математичні моделі реального світу, якими вони виступають, це вміння знаходити вихід із ситуацій, які нам ставить життя.
Ви отримали завдання – підготувати різні способи розв’язання даного рівняння.Під час своїх презентацій дотримуйтесь культури математичного мовлення та письма, не забуваючи про розділові знаки та відповідь.
ІІІ. Представлення результатів своїх досліджень
1.Спосіб універсальної тригонометричної підстановки.
![]()
Нехай ![]() . Застосуємо формули :
. Застосуємо формули :
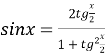 ,
, 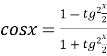 ,
,
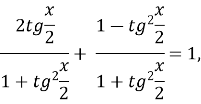
![]() ,
,
![]()
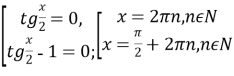 .
.
Перевіркою встановлюємо, що ![]() не є розв’язкою рівняння.
не є розв’язкою рівняння.
Відповідь :![]()
2. Спосіб введення допоміжного кута (аргументу)
![]() .
.
Помножимо обидві частини рівняння на число ![]() .
.
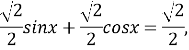
![]() ,
,
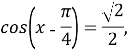
![]() ,
,
![]() .
.
Одержана множина розв’язків збігається з одержаним раніше.
3. Спосіб розкладання на множники.
![]()
Дане рівняння можна записати так:![]() .
.
Оскільки ![]() ,
,
то ![]()
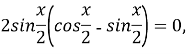
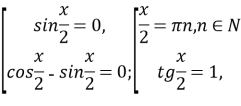
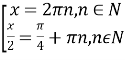 ,
, 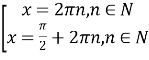
4.Зведення рівняння до однорідного рівняння відносно синуса та косинуса.![]() .
.
Розкладемо ліву частину за формулами подвійного аргументу, а праву частину замінимо тригонометричною одиницею:
![]() ,
,![]()
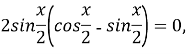
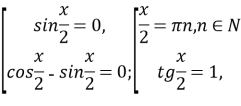
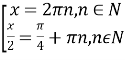 ,
, 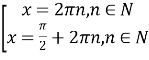
Усі перетворення були рівносильними, тому необхідності перевірити корені немає.
Відповідь :![]()
5.Зведення до однієї тригонометричної функції
![]()
Оскільки ![]() , то
, то
![]()
![]()
Піднесемо обидві частини останнього рівняння до квадрата:
![]()
![]()
![]()
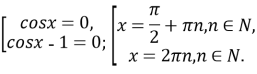
Піднесення до квадрата могло призвести до появи сторонніх коренів, тому необхідно виконати перевірку:
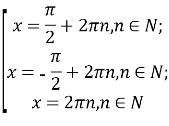
Якщо![]() , то
, то![]() . Корінь підходить.
. Корінь підходить.
Якщо ![]() ,то
,то![]() . Корінь сторонній.
. Корінь сторонній.
Якщо ![]() , то sin
, то sin![]() + cos
+ cos![]() =0+1=1. Корінь підходить
=0+1=1. Корінь підходить
Відповідь :![]()
Музична пауза. Зараз ви прослухаєте фрагмент пісні до відомого кінофільму. А можливо хтось знає як пов’язана тематика фільму із сьогоднішньою датою – 10 квітнем.
10 квітня 1912 року в своє перше й останнє плавання вирушив величезний корабель Титанік, сумна історія якого звучить неймовірно і досі. Вже через кілька днів він потонув, і 15 квітня.
Багато людей знають про круїзний лайнер “Титанік” тільки те, що показав у своєму однойменному фільмі режисер Джеймс Кемерон.
А саме, що він був наймасштабнішим кораблем, побудованим на той момент, що потрапити на нього коштувало немалих коштів, і що в першому ж своєму плаванні він зазнав аварії, зіткнувшись з айсбергом.
Але, крім цієї трагічної історії, є ще багато цікавих фактів про Титанік, які ми досі не знали.
Довжина Титаніка приблизно така ж, як висота 103 поверхового хмарочосу.
Запуск Титаніка не супроводжувався традиційними ритуалами “на удачу”
Ось, у чому вся біда. Коли корабель вирушав у своє перше й останнє плавання, об його борт не розбивали пляшку шампанського.
Крім того, на початку 20-го століття було прийнято заводити кішок на борт, тому що вони допомагали впоратися з гризунами. А ще вважалося, що вони приносять удачу і оберігають судно від неприємностей.
Як ви вже здогадалися, на Титаніку не було жодної кішки. Зате було дев’ять собак, дві з яких пережили аварію корабля.
За 14 років до трагедії був опублікований роман, що описував схожі події. Трагедія, що спіткала Титанік в ніч з 14 на 15 квітня 1912 року, була описана Морганом Робертсоном в його романі “Марність, або Загибель Титана” ще у 1898 році. Вигаданий корабель мав також схожий дизайн з реальним Титаніком, і затонув він при таких же обставинах – зіткнувся з айсбергом холодної квітневої ночі. І навіть ділянка краху збігається – 740 км від Ньюфаундленду в північних водах Атлантичного океану.
Крім того, і в романі, і в реальному житті більше половини людей загинуло через те, що на кораблі було недостатньо рятувальних шлюпок.
Не дивно, що вахтери не змогли помітити величезний айсберг, що пливе в їх сторону, заздалегідь. Адже у них навіть не було біноклів.
Дивно, що при такому масштабі будівництва і прагненні зробити корабель непотоплюваним, забули про таку маленьку, але дуже важливу деталь.
Ось і вийшло так, що після того, як айсберг був помічений, пройшло всього 37 секунд до зіткнення з ним.
Титанік тонув 2 години 40 хвилин. Він опускався на дно зі швидкістю 16 км / год. Зараз він спочиває на глибині 3750 м.
Багато пасажирів Титаніка повинні були плисти на інших кораблях
Температура води була близько -2 °C,
У такій холодній воді мало хто міг би протриматися більше 15 хвилин.
6.Перетворення суми тригонометричних функцій у добуток .
![]()
Запишемо рівняння у вигляді ![]() .
.
За формулою різниці двох синусі в, одержимо:
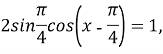
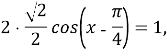
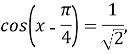
![]() +
+![]()
![]()
7.Піднесення до квадрата обох частин рівняння .
![]()
![]() ,
,
![]()
![]()
![]()
![]()
Перевіримо чи не одержали сторонніх коренів.
Якщо![]() , то sin
, то sin![]() + cos
+ cos![]() =0+1=1.
=0+1=1.
Якщо![]() , то sin
, то sin![]() + cos
+ cos![]() =1+0=1
=1+0=1
Якщо![]() , то sin
, то sin![]() + cos
+ cos![]() =0-1=-1
=0-1=-1![]() . Сторонній корінь
. Сторонній корінь
Якщо ![]() ,то sin
,то sin![]() + cos
+ cos![]() =-1+0=-1
=-1+0=-1![]() . Сторонній корінь.
. Сторонній корінь.
Відповідь :![]()
8.Графічний спосіб.
![]()
Перепишемо дане рівняння у вигляді ![]() .
.
Побудуємо графіки функцій![]()
![]() . Абсциси точок перетину цих графіків будуть розв’язками даного рівняння.
. Абсциси точок перетину цих графіків будуть розв’язками даного рівняння.
Відповідь : ![]()
ІV. Перевірка рівня засвоєння знань.
Встановити відповідність між рівняннями та їх розв’язками:
![]()
![]()
![]() B.
B.![]()
![]() Б.
Б.![]() +2
+2![]()
![]() Д..
Д..![]()
Г.![]()
V. Підсумок уроку.
Ви вже дорослі і чудово розумієте, що коли учень знайшов один спосіб розв'язання задачі й правильно його застосував — це досягнення та успіх, а коли знайдено декілька способів, то коментарі зайві. Розв'язуючи запропоноване вам рівняння, ми знайшла 8 способів його розв'язання, тож пропоную вам вдома знайти спосіб, що відрізняється від тих, які сьогодні розглядалися на уроці.
Від душі бажаю вам у майбутньому бачити декілька варіантів розв'язання не тільки математичних задач, а й життєвих проблем і неодмінно вибирати найраціональніший.
VI. Домащнє завдання. 1.Розв’язати кількома способами рівняння ![]() .
.
2.Знайти помилку в міркуваннях:
![]()
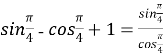 ,
,
![]()
![]()
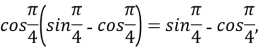
![]()


про публікацію авторської розробки
Додати розробку
