"Застосування похідної"

Тема уроку: «Застосування похідної»

 

Мета уроку:

• узагальнити та систематизувати  вивчені відомості про похідну; формувати вміння застосовувати набути знання при розв’язання прикладних задач;  поглибити знання учнів про моделювання процесів дійсності за допомогою похідної;
• розвивати пізнавальний інтерес,  логічне мислення, оперативність при виконанні вправ,  бажання мати якісні, глибокі знання;
• виховувати працьовитість, зібраність, увагу, відповідальність та вимогливість до себе.

Тип уроку: узагальнення та систематизації знань.

Обладнання: комп’ютер, проектор.

 

                                            «Об’єкт математики  настільки серйозний, що слід     

не пропускати нагоди зробити його трохи цікавішим»

Б. Паскаль

 

ХІД УРОКУ

І. Організаційний етап.

       Сьогодні у нас останній урок з теми. Готуючись до уроку, ви об’єдналися в групи, отримали проблемні завдання. Сподіваюсь, що ви гарно підготувались до уроку і зможете продемонструвати знання теоретичного матеріалу, розуміння вивченого, уміння використовувати отримані знання при розв’язанні задач, навички самоконтролю  та самооцінки.

 Пам'ятка для учня нехай допоможе вам психологічно налаштуватися на урок.

 

Пам'ятка для учня

 

• Визнач властивий ступінь оволодіння навчальним матеріалом.
• Будь уважним, май гарний настрій.
• Будь наполегливим і не бійся помилятись.
• Міркуй самостійно, твори і дій.
• Пробуй оцінити себе об'єктивно.

 У кожного з вас є картка самоконтролю, не забувайте за участь у кожному  етапі уроку виставляти собі оцінку.

 

ІІ. Мотивація навчальної діяльності.

   Вона на вигляд недолуга:

   Штришок маленький, та й усе,

   Але яку значну потугу

   Цей ледь помітний знак несе!

   Це символ моря знань високих,

   Який не має меж і дна.

   Не ступите не раз ні кроку

   Без терміну, що зветься “похідна”.

    На попередніх уроках ви засвоїли один із фундаментальних понять алгебри і початків аналізу – похідну. За допомогою похідної ми досліджували і будували графіки функції, знаходили найбільше і найменше значення функції на відрізку, складали рівняння дотичної, розв’язували задачі.  І, мабуть, у вас виникало питання: «А навіщо? Як використовується похідна в повсякденному житті?»

І наш урок буде відповіддю на це запитання.

 

 ІІІ. Актуалізація опорних знань.

Для того, щоб нам  успішно провести урок необхідно повторити теоретичний матеріал.  Перший етап нашого уроку пройде під девізом « Хай живе теорія».

Фронтальне опитування «звездопад»

1. Що ми називаємо диференціальним численням?
2. Дайте означення похідної функції в точці.
3. У чому полягає механічний зміст похідної ?
4. У чому полягає геометричний зміст похідної?
5. Чому дорівнює кутовий коефіцієнт прямої ?
6. Як називаються точки    мінімуму і максимуму?
7. Як називається точка, якщо при переході через стаціонарну точку похідна міняє знак  з “-” на “+”?
8. Як називається функція, похідна якої дорівнює cosx?
9. Як називається функція, задана формулою у = f(g(x))?
10.  Як називається внутрішня точка області визначення функції, у якій функція неперервна і  похідна дорівнює нулю?

«Мало мати гарний розум,

головне добре його застосовувати»

Рене Декарт

Другий етап уроку «Тестування».

Завдання мають п’ять відповідей, серед яких лише одна правильна:

 

Тестування по темі «Похідна»

1. Знайти похідну функції:

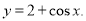
А	Б	В	Г	Д
		1 – 2

2. Для якої з наведених функцій справедлива рівність ?

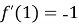А	Б	В	Г	Д
f(x)=x2+1	f(x)=x2-1		f(x)=x3

3. Точка рухається за законом  S(t)=1+2t² (м). Знайдіть швидкість руху точки в момент t= 1 с.

А	Б	В	Г	Д
2 м/с	3 м/с	4 м/с	4,5 м/с	5 м/с

4. Знайдіть кутовий коефіцієнт дотичної, проведеної до параболи у=х²+х    у точці з абсцисою х₀.

А	Б	В	Г	Д
2х0+1	2х0	2	1	2х0+2

5. Дотична до графіка у= f(x) у точці з абсцисою х₀ утворює з додатним напрямом осі Ох кут 45⁰. Знайдіть f ^/(x₀).

А

Б

В

Г

Д

-1

0

1

-2

2

6. Знайдіть значення похідної функції 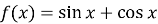у точці х₀=0.

А	Б	В	Г	Д
-2	-1	0	1	2

7.  Знайдіть значення похідної функції 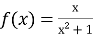у точці х₀=0.

0	-1	1	-2	2

8. Знайдіть точки екстремуму функції .

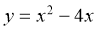А	Б	В	Г	Д
2	-4	4	0,4	0,04

9. Знайдіть похідну функції  у= сos (3-2x).

А	Б	В	Г	Д
sin(3-2x)	2sin(3-2x)	3sin(2-3x)	-2sin(3-2x)	3sin(2-3x)

10. Знайдіть абсцису точки графіка функції 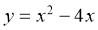, у якій дотична до цього графіка паралельна прямій .

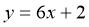А	Б	В	Г	Д
1	5	3	-1	-3

Перевірка: шляхом взаємоперевірки.
 

1	2	3	4	5	6	7	8	9	10
Г	В	В	А	В	Г	В	Д	Б	Б

 

Підводимо підсумок цього етапу уроку

Чи всі задоволені результатом роботи? Чи багато помилок допустили?

Український письменник Г. С. Сковорода писав: «Найкраща помилка та, яку допускають під час навчання». Дуже часто показником успіху в житті є не тільки кінцевий результат, а і процес його досягнення.

 

ІV. Розв’язання вправ.

 

Як використовується похідна в повсякденному житті?

 

ГРУПА «ІСТОРИКИ»

 Подібно тому, як Архімед відкривши закон важеля, сказав: «Дайте мені точку опори і я зрушу Землю», так і сучасники Ньютона казали: «Складіть нам диференціальне рівняння усіх рухів у природі і навчіть їх інтегрувати, тоді ми будемо подібні Богу, оскільки за допомогою обчислень точно будемо знати майбутні події».                 Д.О.Дравс

         Середина XVII століття сталося найвидатніше відкриття усіх часів — створення нової математичної теорії: диференціального та інтегрального числення.

        І все життя полетіло так швидко, що вчені не могли навіть уявити такого.

 Розвиток науково-технічного прогресу, війни, виготовлення зброї, епідемії і відкриття цілющого пеніциліну, запуск космічної ракети і створення ядерних реакторів – основою цього всього послужило диференціальне числення. Від високих досягнень  до стрімких падінь крокувала поряд похідна, кидаючи свої максимуми і мінімуми¸ похідна, яка миттєво змінила світ.

  За допомогою диференціального числення було розв’язано багато задач теоретичної механіки, фізики, астрономії. Зокрема , використовуючи методи диференціального числення , вчені передбачили повернення комети Галлея, що стало тріумфом науки XVIII ст.

        І тепер поняття похідної широко застосовується у різних галузях науки та техніки.

Висновок : «Без диференціального числення математика, як наука, не могла б досягти сучасного свого розвитку» Х.Гюйгенс

 

 

 

ГРУПА «СТАТИСТИ»

 

Статистика – річ сувора з нею не посперечаєшся.

         Ми отримали завдання: проаналізувати вміст теми «Похідна» в шкільної програмі та в екзаменаційних  завданнях.

         В курсі вивчення «Алгебри та початків аналізу» у 10 – 11 класі тема «Похідна» займає 15%.

      В екзаменаційних завданнях, вміст завдань на тему «Похідна» складає 14%

Висновок: Вивчення теми «Похідна» необхідне для подальшого життя.

 

ГРУПА «ПРАКТИКИ»

     «Найкращий спосіб вивчити що-небудь –  відкрити його самостійно»

                         Дьордь Пойа

            Ми розглядали  завдання, які пов'язані з застосуванням математики в техніці, хімії, економіці, медицини, екології, побуті та які можна вирішити за допомогою похідної.

            Похідна характеризує швидкість зміни функції по відношенню до зміни незалежної змінної. В геометрії похідна характеризує кривизну графіка, в механіці - швидкість нерівномірного прямолінійного руху, в біології - швидкість розмноження колонії мікроорганізмів, в економіці - вихід продукту на одиницю витрат, в хімії - швидкість хімічної реакції.
 

При розв’язуванні задач :

1. Треба зрозуміти задачу
2. Знайти зв’язок між відомими та невідомими
3. Скласти план розв'язання та виконати його
4. Проаналізувати розв'язок задачі

               «Уміє розв’язувати задачі той, хто їх розв’язує»

Дьордь Пойа   

Висновок: Похідна дає змогу розв'язувати багато прикладних задач.

                        

Задача№ 1

У повісті І.П.Котляревського «Енеїда».

 Еней після багатьох пригод пристав до берега і потрапив до міста.

 В тім городі жила Дідона,

 А город звався Карфаген,

 Розумна пані і моторна,

 Для неї трохи сих імен:

 Трудяща, дуже працьовита,

 Весела, гарна, сановита.

 

Так розповідає легенда. 825 років до н.е. фінікійська царівна Дідона з невеликим військом вибрала зручне місце на північному узбережжі Тунійської затоки. Король Нумібії Ярб погодився  продати їй ділянку землі, обмежену «шкурою бика». Дідона не розгубилася. Вона розрізала шкуру на тоненькі смужки, якими обміряла територію найбільшої площі. Так було засновано Карфаген.

Якщо вважати, що шкіра вола матиме розмири 4 м² та Дідона різала її на смужки по1мм спірально, то вона мала смужку довжиною 4 км.

        Задача № 1 

 Обчислити яку найбільшу площу мале Карфаген, якщо однієї стороною він примикає до моря та мале форму прямокутника ( 2 км²)

         Задача № 2
При виверженні вулкану камені гірської породи викидаються перпендикулярно вгору з початковою швидкістю 120 м / с. Якої найбільшої висоти досягне каміння, якщо опором вітру знехтувати?  (734,4 м)

       Задача № 3.

Дріжджі ростуть  у цукровому розчині так, що їх маса збільшується на 3% за кожну годину. Знайдіть найбільше значення маси дріжджів через 10 хвилин, якщо її початкове значення 1 гр. (1,005 гр)

 

 

ГРУПА «ДОСЛІДНИКИ»

 «Усе, що пізнаю, я знаю, для чого це мені потрібно,

де і як можу застосувати ці знання».

                        В.Кильпатрик

 

Проблемна  задача : На якій висоті потрібно встановити ліхтарі, щоб краще освятити вулицю, якщо відстань між ліхтарями 30 м. 

 

V. Підсумок уроку

 

Саме час повернутися до початку уроку, до мети, яку ми перед собою поставили. Поміркуйте, чи досягли ви її, чи відтворили знання про похідну, чи перевірили свої навчальні досягнення  під час виконання завдань?

 

Ці задачі не прості:

Застосуєш їх в житті.

Ну а щоб їх розв’язати –

Похідну треба вивчати.

Висновок: Одним з найважливіших понять математичного аналізу є похідна функції.

 

VІ. Домашнє завдання

 

Поставтесь відповідально до виконання домашнього завдання, оскільки з повторенням кожного означення,  твердження,  формули,  з виконанням кожного завдання ви наближаєтесь до досягнення мети, до успішної здачі ЗНО, що є дуже важливим для вас.

 

« НЕ МАХАЙ НА ВСЕ РУКОЮ, НЕ ЛІНУЙСЯ, А УЧИСЬ,

БО ЧОГО НАВЧИШСЯ В ШКОЛІ, ЗНАДОБИТЬСЯ ЩЕ КОЛИСЬ!»