Тема: Елементарні геометричні фігури та їх властивості

Урок 5.

Бісектриса кута.  Рівність кутів.

Мета:

• засвоїти  нові поняття «внутрішній промінь кута, бісектриса кута»;
• опанувати  особливості вимірювання кутів, що розбиваються на дві частини своїм внутрішнім променем;
• формувати навики  будувати бісектрису за допомогою транспортира;
• розвивати вміння розв’язувати типовi задачi з теми «Бісектриса кута».

 «... арифметика і геометрія значно достовірніші, ніж усі інші науки, а саме — предмет їх настільки зрозумілий і простий, що вони зовсім не потребують ніяких припущень, які досвід може піддати сумніву, а цілком складаються з послідовного виведення міркуваннями.»                                            Рене Декарт

Рене́ Дека́рт (31 березня 1596  — 11 лютого 1650) — французький філософ, фізик, фізіолог, математик, основоположник аналітичної геометрії.

Методичні рекомендації

Дана тема  рекомендована для тих учнів, які мають намір самостійно вивчити і опрацювати тему «Бісектриса кута. Рівність кутів.», з подальшим розв’язанням практичних завдань. Вчитись застосовувати аксіому вимірювання кутів при розв’язуванні вправ.

Тема та структура матеріалу повністю відповідають навчальній програмі з математики за курс  базової школи.             

Матеріали до уроку

1. Бісектрисою кута називається промінь, який виходить із вершини кута і поділяє його на два рівних кути.

БІСЕКТРИСА (від лат. bis — «двічі» та лат. seco — «розтинаю»).

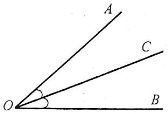
Наприклад: промінь ОС – бісектриса кута АОВ, оскільки  (рівні кути на мал. позначають однаковими дужками).

2. Чи є промінь ОК – бісектрисою ∠ AОB? 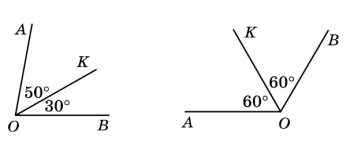        Відповідь: ні;  так
3. Побудова бісектриси кута

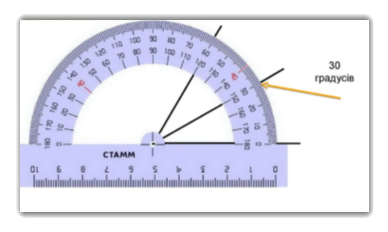
4. Виконання графiчних вправ

1. Накреслiть кут ABC, що дорiвнює 100°.

а) Проведiть бiсектрису BD цього кута. Якою є градусна мiра кута DBC?

б) Перегнiть рисунок по прямiй BD. Чи збiгаються променi BA i BC? Як це пояснити?
    Відповідь: а) ∠DBC=50°;  б) кути рівні, промені збігаються.

2. Накреслiть кут ABC, що дорiвнює 100°. Проведiть промiнь BD, який подiлив би кут ABC на два кути, градусна мiра одного з яких на 20° бiльша за градусну мiру iншого.

Р о з в ’ я з а н н я: ∠ ABC=∠ ABD + ∠ DBC,   ∠ ABD=x, ∠ DBC= x+20,

x + x + 20 = 100,  2x = 80,  x=40.

∠ ABD = 40°,   ∠ DBC = 60°.

5. Розв’язування задач

Задача: ∠ ABC = 100°, BK — бісектриса кута ABC, а BL — бісектриса кута KBC.

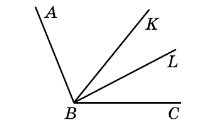Знайти ∠ ABL.

Р о з в ’ я з а н н я

1) ∠ KBC =∠АВС:2 =100:2 = 50°;

2) ∠ LBC =∠КВС:2 = 50:2 = 25°;

3) ∠ ABL = ∠ ABC – ∠ LBC = 100° – 25° = 75°.

В і д п о в і д ь. 75°.

1

Запам’ятайте! Рівні кути мають рівні градусні міри. Якщо два кути мають рівні градусні міри, то ці кути рівні.

Більший кут має більшу градусну міру. З двох кутів більший той кут, градусна міра якого більша.

Приклади розв’язування вправ

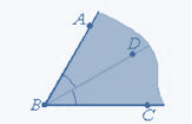1. Промiнь BD—бiсектриса кута ABC. Знайдiть кути ABC i ABD, якщо кут ABC бiльший за кут DBC на 38°. 

Рішення: BD—бiсектриса кута ABC, то
∠ ABD=∠ DBC = 38°, тоді ∠ABD = 2∠DBC =76°.

2)  Промiнь b дiлить кут (ac), який дорiвнює 150°, на два кути. Знайдiть кути (ab) i (bc), якщо кут (ab) менший за кут (bc) на 40°.

Рішення: За аксіомою вимірювання кутів
∠ (ac) =  ∠(ab) + ∠(bc).
Нехай ∠(ab) = х°, тоді ∠(bc) = х° + 40°.
х  + х + 40 = 150, 2х = 110, х = 55.

Отже, ∠(ab) = 55°, ∠(bc) = 95°.
Відповідь: ∠(ab) = 55°, ∠(bc) = 95°.
 

3)  Промiнь k — бiсектриса кута (mn). Знайдiть кут (mn), якщо кут мiж бiсектрисами кутів (mk) i (kn) дорiвнює 70°.

Рішення: Бісектриси кутів (mk) i (kn) розділили їх на два рівних кута відповідно. За умовою, кут мiж бiсектрисами кутів (mk) i (kn) дорiвнює 70°, тоді  ∠(mn) = 2 ∙ 70° = 140°.

Відповідь: 140°.

Самостійно розв’язати:

1. Промiнь b дiлить кут (ac) на два кути. Знайдiть кут (ab), якщо , .

2. Промiнь b — бiсектриса кута (ac). Знайдiть:

а) кут (ac), якщо ;

б) кут (ab), якщо  прямий.

3. Промiнь OB дiлить кут AOC, що дорiвнює 120°, на два кути. Знайдiть кути AOB i BOC, якщо градуснi мiри кутiв вiдносяться як 3 : 5.