Урок "Розв'язування задач з теми "Кути"

Тема: Елементарні геометричні фігури та їх властивості

Урок 6

РОЗВ'ЯЗУВАННЯ ЗАДАЧ
 

• формувати вміння розв’язувати типовi задачi на застосування аксiом вимiрювання та вiдкладання кутiв;
•  вiдпрацювати навички побудови кутiв та їх вимiрювання iз використанням приладiв.

Не в кількості знань полягає освіта, а в повному розумінні й майстерному застосуванні всього того, що знаєш.                                Дістервег

Фрі́дріх Адо́льф Вільге́льм Дістерве́г ( 29.10.1790  — 07.07.1866, Берлін) — видатний німецький педагог-демократ, послідовник Песталоцці.

 Методичні рекомендації:

Дана тема  рекомендована для тих учнів, які мають намір самостійно вивчити і опрацювати тему «Кут. Вимірювання та відкладання кутів. Бісектриса кута.», з подальшим розв’язанням практичних завдань. Опрацювати властивості вимірювання кутів, розв’язувати завдання на знаходження градусної міри кута. Тема та структура матеріалу повністю відповідають навчальній програмі з математики за курс  базової школи.    

    Матеріали до уроку

Пригадайте:

1.Наука про властивості геометричних фігур - …

2.Що в геометрії позначають однією великою латинською літерою?

3.Який кут дорівнює 90°?

4.Через дві точки можна провести пряму… .

5.Чому дорівнює градусна міра кута?

6.З трьох точок на прямій одна і тільки одна… .

7.Пряма розбиває площину на дві….

8.Фігура, яка складається з трьох точок і трьох відрізків, що їх

сполучають, називається… .

9. Твердження, яке приймається без доведення, називається… .

10. Бісектриса кута – це промінь … .
 

Розв’язування вправ:

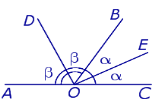1. Дано розгорнутий кут АОС і його внутрішні промені. Назвіть їх.
   Які з внутрішніх променів є бісектрисами?
   Бісектрисами яких кутів вони є?    

(Відповідь: ОЕ – бісектриса кута ВОС;

                    ОD – бісектриса кута АОВ)

2.          Дано  кут АОР. Промінь ОМ – бісектриса кута АОP.

Чи вірно, що…

А) 2 ∠POM = ∠AOP;          Б) ∠AOM = ∠POA;            В) ∠MOA = ∠AOP.

(Відповідь: так; ні; ні)

3. Промінь ОС ділить  ∠АОВ = 120° на два кути так, що один із них на 30° менше  другого. Знайти градусну  міру ∠АОС  та  ∠ВОС.

Рішення:

1. ∠АОС + ∠ВОС = ∠АОВ (за властивістю вимірювання кутів)
2. Нехай ∠ВОС = х°, тоді ∠АОС = х° + 30°

Маємо: х + х + 30 = 120,

2х + 30 = 120,

2х = 90,

х = 45.      Отже,  ∠ВОС = 45°, ∠АОС = 45° + 30° = 75°.

4. Промінь b ділить кут (ас), який дорівнює 150°, на два кути. Знайдіть кути (аb) і (bс), якщо ∠(аb) менший за ∠(bс) у 4 рази .  

Рішення:

∠(аb) + ∠(bс) = ∠(ас)   (за властивістю вимірювання кутів)

∠(аb) = х°,     ∠(bс) = 4х°, тоді    х + 4х = 150, х = 30.
Отже,   ∠(аb) = 30°,     ∠(bс) = 120°.

Розв’язати самостійно:  

1. Промінь ВД – бісектриса кута АВС. Знайдіть ∠АВС і  ∠АВД, якщо ∠АВС більший за ∠ДВС на 38° .
2. Промені ОВ і ОС ділять кут АОD на три кути. Знайдіть кут ВОС, якщо ∠АОD = 110°, ∠АОС = 85° , ∠ВОD = 60°.
3. Промінь  ОС ділить  ∠АОВ = 80º на два кута так, що один із них у 3 рази більше другого.  Знайти  ∠АОС  та  ∠ВОС. 
4. Знайдіть градусну міру кута між годинною та хвилинною стрілками годинника:   1) о 21 год;    2) о 6 год;      3) о 19 год;      4) о 2 год.