Урок "Числові множини"

Про матеріал

Дана розробка для 8 класу (урок алгебри) на тему "Числові множини" містить логічну вправу, ігровий момент та набір матеріалів до уроку для друку.

Перегляд файлу

Вчитель:Ткачик З.Л.

Тема: Раціональні, ірраціональні, дійсні числа. Числові множини (слайд 1)

Мета: Систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами. Розвивати уміння аналізувати та спів ставляти ознаки чисел при визначенні належності їх до певної множини. Виховувати зосередженість, увагу.

Тип уроку: комбінований.

Наочність та обладнання: Опорний конспект «Дійсні числа», конверти з назвами множин, карточки з різними числами.

Девіз уроку: Намагайся завжди знати більше!

Хід уроку

І. Організаційний етап.

Учитель. Сьогодні ми не будем сумувати,

А будем числові множини розширяти!

Я сподіваюся на вашу дисциплінованість, активність, уважність.

ІІ. Актуалізація опорних знань.

Бесіда з учнями «Мікрофон»

Які числа ви уже вивчали? (Додатні, від’ємні, дробові, цілі)
Як ще можна назвати цілі додатні числа? (Натуральні)
Як перетворити звичайний дріб у десятковий? (Чисельник поділити на знаменник)
Які десяткові дроби при цьому можуть утворитись? (Скінченні і нескінченні)
Які є види нескінченних дробів? (Періодичні та неперіодичні)

Усні вправи (слайд 2,3)

Знайдіть значення виразу: 5² ; (-5)² ; -5² ; 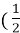)³ ;)³ ; 0².
Обчисліть: ; ; - ; ; ; .
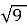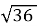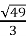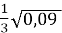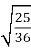Розв’яжіть рівняння: а²=25 ; к² = 0,49; b²=-9 ;c²=7.

ІІІ. Мотивація навчальної діяльності. (слайд 4)

Логічна вправа

Вставте пропущену літеру: 1; -5 ; 0 ; 6 ; 11 ; -2 ; -7 . Z

2 ; -7 ; ; ; 0 ; ; -1. ?

IV. Засвоєння нових знань.

( слайд 5)

Числа, які використовують при лічбі, тобто, додатні цілі числа, називають натуральними числами. Їх безліч, але всі вони записуються за допомогою десяти цифр: 1;2;3;4;5;6;7;8;9;0. За допомогою даних цифр можна зібрати числа, які використовують при лічбі, у деяку сукупність. І, кажуть,що такі числа утворюють множину натуральних чисел. Самі ж числа є елементами цієї множини.

(слайд 6)

При додаванні та множенні натуральних чисел завжди дістають натуральне число. А ось при відніманні -- не завжди. Тому щоб завжди виконувалась дія віднімання ввели від’ємні числа та число нуль. Таким чином , натуральні числа, протилежні їм, число нуль утворюють множину цілих чисел. Ця множина позначається літерою Z.

(слайд 7)

При додаванні , множенні та відніманні цілих чисел завжди отримують ціле число. Але під час ділення двох цілих чисел не завжди отримаємо ціле число. Тому множину цілих чисел доповнили ще й дробовими. Після чого в отриманій множині вже виконувались усі чотири арифметичні дії. Назвали цю множину множиною раціональних чисел та позначили літерою Q . Термін «раціональне число» походить від латинського слова Ratio, що означає відношення, частка. Отже, число,яке можна подати у вигляді дробу , де m – ціле число, а n – натуральне, називається раціональним числом.

Взагалі, кожне раціональне число можна різними способами подати у вигляді дробу . Наприклад: а) = =…= =… б) - =- =…=- =…

Кожен дріб , де m – ціле число, а n – натуральне, можна подати у вигляді скінченного десяткового дробу, або періодичного десяткового дробу .

(слайд 8)

Однак, крім скінченних десяткових дробів та періодичних десяткових дробів є ще і нескінченні неперіодичні дроби . Такі дроби називають ірраціональними числами.

Цікавий факт : слово «раціональний» (від лат.rationalas) у буквальному перекладі з латини означає «розумний», «пов'язаний з відношенням». А термін ірраціональний, тобто нерозумний, несумірний, утворено приєднанням латинського слова ir – «не», «без». Виникнення такої назви пов’язане з тим,що математики не відразу з’ясували зміст цих чисел та не вважали їх рівноправними звичайним числам.

(слайд 9)

Ірраціональні та раціональні числа разом утворюють множину дійсних чисел і кожне її число називають дійсним числом. Позначають множину дійсних чисел літерою R.

(слайд 10)

Якщо розширення поняття числових множин зобразити у вигляді перетину деяких кругів , то картинка буде такою:

N, Z, Q, R.

V. Формування вмінь.

1. Фізкультхвилинка

Учитель називає довільне число, підіймає будь-якого учня і він повинен вказати до якої множини належить дане число. Решта учнів, якщо той відповів правильно, плескають.

Наприклад: називаю число (-10) . Якщо учень називає його цілим, раціональним або дійсним, то решта учнів плескають, якщо натуральним - то ні.

Повторити кілька разів, щоб бачити,чи учні зрозуміли новий матеріал.

Робота з підручником.

Усно: № 668, 669. Письмово: № 676 а) 49; 1; 3 ; б) 49; 1; -2,5; 3; 0 ; в) ; ; г); ; 49; -1,21; 1; -2,5; 3;0; .

№ 678

а) 0,7 = ; б) 0,53 = ; в) 3 = ; г) 1,25 =1 .

№ 680

Подайте число у вигляді нескінченного десяткового дробу:

а) = 0,66666…= 0,(6) ; б) = 0,83333…=0,8(3) ; в) = 1,06666…= 1,0(6) ;

г) =3,1666…= 3,1(6) ; д) =0,14285714285714…= 0,(142857) .

Порівняйте числа:

№ 682

1) ˂ 2) ; 3) - ˃ -

№ 683

1) 0,66; 2) 0,67 ; 3) = 0,6666…

№ 685.

1)π 3,14 (π=3,1415926…) ; 2) π (= 3,85714…)

3) π (= 3,16227766…)

3. Ігровий момент

«Математичний баскетбол»

Клас ділиться на дві команди. Кожна команда має свій набір карток (картки двох кольорів). На столі ,на двох купках, лежать картки, на яких написані різні числа, числами донизу. На дошці прикріплені корзини (файли) з вставленими листками, на яких написані літери, що позначають множини: N, Z, Q, R. Діти по черзі вибирають навмання картку з числом і кидають у відповідну корзину (файл). Яка команда більше правильно розподілить чисел, та виграла.

VІ.Підсумок уроку.

1.Вставити літеру R в логічній вправі.

2. Оцінювання учнів.

VІІ. Домашнє завдання.