Урок "Декартові координати і вектори у просторі."

Тема уроку:  Декартові координати і вектори у просторі. Ділова гра – аукціон в 10 класі.

Мета:  узагальнити і систематизувати знання та вміння учнів з теми; виховувати інтерес до геометрії та ринкової економіки.

Тип уроку: узагальнення та систематизація знань.

Методи: колективна діяльність, індивідуальна робота, ділова гра.

Обладнання:  таблиці, картки, підручник.

Ділова гра – це імітаційна модель навчальної діяльності учнів, що відтворюється в умовах, наближених до дійсності. Мета ділової гри – поглибити та розширити діапазон знань учнів, формувати діловий стиль спілкування у практично-професійній діяльності. Незалежно від різновидів таких уроків, їх об’єднують загальні вимоги: постановка теми, цілей та завдань гри; визначення оптимального змісту гри; розподіл ролей та визначення функціональних обов’язків учасників гри; забезпечення умов для проведення. Класний варіант гри включає три етапи : підготовка, сама гра, аналізу та підбиття підсумків.

План уроку

І. Організаційний момент.

Мотивація навчальної діяльності учнів.

ІІ. Основна частина уроку (Дидактична гра – аукціон). Повторення та систематизація знань з теми «Декартові координати і вектори в просторі»

ІІІ. Підсумок уроку.

IV. Домашнє завдання.

Хід уроку

І. Організаційний момент.

Учитель оголошує тему та мету уроку, надає учням інформацію про аукціон, розповідає, що таке лоти та стартова ціна.

На кожну парту роздається аркуші з переліком лотів до продажу.

ІІ. Аукціон.

Учням пропонується купити той чи інший лот і оголошується ціна:

0,5 бала, якщо інформацію до нього подано у підручнику;

1 бал, якщо було уточнення з боку однокласника чи вчителя;

2 бали, якщо учень дав відповідь самостійно і в повному обсязі.

 

Лоти, що виставляються на продаж.

 

Блок №1

 

1.                     Означення декартових координат у просторі.

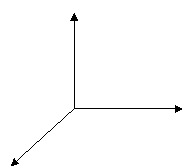
1.                     Пояснити, як вводяться Декартові координати у просторі, що таке початок координат і координатні осі, вказати їх напрями, назвати координатні площини.

 

Нехай x,y,z – три попарно перпендикулярні координатні прямі, які перетинаються в точці О.

 

Назвемо їх координатними осями: «вісь х», «вісь у», «вісь z». Точка О – початок координат. Кожна вісь точкою О розбивається на дві півосі – додатню, позначеною стрілкою, і від’ємну

 

Площини, які проходять через осі x і y, x і z, y і z, –– координатні площини. Позначають їх відповідно: xy, xz і yz. Осі називають вісь абсцис, вісь ординат, вісь аплікат. Координатні площини розбивають весь простір на вісім октантів.

 

2.         Дано точки А (0;3;1), В (-2;0;0), С (0;0;4), Д (0;-3;0). Які з них лежать : 1) на осі X; 2) на осі 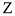; 3) у площині 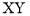; 4) у площині ?

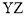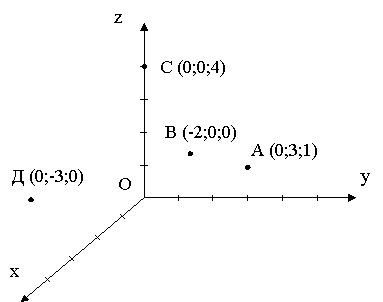
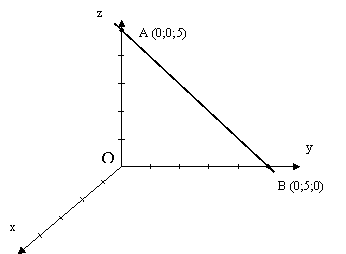
3.         Зобразити у системі координат пряму, яка проходить через точки А (0;0;5) і В (0;5;0)

 

 

2.                     Координати середини відрізка.

1.         Сформулювати і записати формулу, чому дорівнюють координати середини відрізка у просторі.

Квадрат відстані між двома точками дорівнює сумі квадратів різниць їх відповідних координат.

Нехай дано дві точки А і В, тоді

 

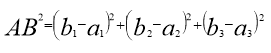
2.         Знайти координати середини відрізка АВ, якщо А (1;2;3) і В (3;-6;7).

Розв’язання:

За формулами координат середини відрізка

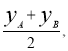х = у = z =

Тому х =

Відповідь : (2;-2;5)

 

 

Точки А (3;-1;-2), В (-5;7;4), С (1;5;2), Д (9;-3;-4) – вершини чотирикутника. Довести, що даний чотирикутник – паралелограм.

Розв’язання

За властивістю діагоналей паралелограма.

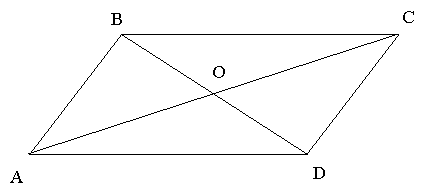
0 – середина АС і ВД.

За формулами координат середини відрізка знайдено координати точки 0.

АС :

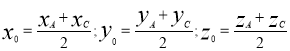
О (2;2;0)

ВД:

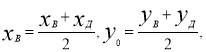
О (2;2;0)

Отже, О – середина АС і ВД, тому АВС – паралелограм.

3.                     Відстань між двома точками.

1.                     Дати словесне формулювання та записати формулу відстані між двома точками.

Нехай С - середина відрізка АВ. Точки А і В - кінець відрізка. Тоді .

Отже, кожна координата середини відрізка дорівнює півсумі відповідних координат його кінців.]

2.                     Знайти відстань між точками В (-2;0;3) і К(3;4;2)

Розв’язання :

За формулою відстані між двома точками

Тому

Відповідь:

3.                     На осі Х знайти точку, рівновіддалену від точок В(3;2;4) і С (0;5;-1).

Розв’язання :

Нехай точка М (х;0;0) рівновіддалена від точок В і С, тоді МВ =МС.

За формулою відстані між двома точками :

Знайдемо відстань МВ і МС

МС.

Розв’яжемо рівняння:

 

; . Отже, М (;0;0).

Відповідь: (; 0;0).

4.                     Рівняння сфери .

1.         Що називається сферою? Записати рівняння сфери з центром у точці А (а;в;с) і радіуса r. Який вигляд має рівняння сфери з центром у початку координат.

Сферою називається геометричне місце точок простору, які віддалені на одну і ту саму відстань r від даної точки. Ця точка – центр сфери, а відстань r – її радіус.

Рівняння сфери радіуса r з центром у точці має вигляд

.

Якщо а=в=с=0, дістанемо рівняння сфери радіуса r з центром у початку координат:              .

2.         Складіть рівняння сфери радіуса r = 5 з центром у точці А (1;0;4).

Розв’язання:

Рівняння сфери має вигляд : 

Рівняння даної сфери буде мати вигляд :

, або

 

Відповідь:

3.         Чи належить точка М (3;2;-1) сфері, рівняння якої

 

 

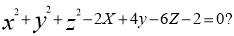
Розв’язання :

Точка М (3;2;-1) х =3; у = 2; z =-1.

Підставимо дані координати в рівняння сфери :

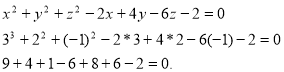
. Тому точка М (3;2;-1) не належить даній сфері.

Блок №2

1.         Вектор, його координати, абсолютна величина, рівні вектори.

1.         Дати означення вектора та його координат, вказати, як позначається вектор, записати координати нульового вектора; виразити абсолютну величину вектора через його координати. Сформулювати означення рівних векторів.

Вектором називається напрямлений відрізок.

Записують або .

Вектори часто задають за допомогою координат. Координати вектора ,початок якого А, а кінець В називають числа .

Записують такий вектор, зазначаючи його координати або .

Два вектора називаються рівними, якщо їх відповідні координати рівні. Якщо всі координати вектора – нулі, то його називають нульовим вектором і позначають символом .

Довжиною, або модулем вектора називають довжину напрямленого відрізка, що зображає його. Позначають довжину вектора символом . Якщо , то .

Довжина будь-якого ненульового вектора – число додатне. Довжина нульового вектора дорівнює нулю].

2.         Дано точки А (1;2;3), В (3;7;6). Знайти координати вектора .

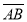Розв’язання:

Координатами вектора , початок якого А (1;2;3), а кінець В (3;7;6) будуть дорівнювати :

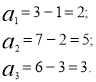
Тому  Відповідь : (2;5;3)

 

3.         Знайдіть координати вектора (а;2а;-а), якщо його абсолютна величина .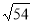

Розв’язання:

Абсолютна величина вектора знаходиться за формулою

, тому 

 

Піднесемо ліву і праву частини рівняння до квадрату :

  

Тоді 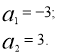Вектор матиме координати. (-3;-6;3) або (3;6;-3).

Відповідь: (3;6;-3) або (-3;-6;3).

 

2.         Додавання та віднімання векторів.

1.         Дати означення суми двох векторів; записати закони додавання. Дати означення різниці двох векторів. Сформулювати відповідні правила.

Сума векторів і називають вектори .

Властивості суми векторів. Для будь-яких векторів справедливі рівності:

1)- переставний закон додавання;

2)- сполучний закон додавання.

Різницею векторів і називають такий вектор , який у сумі з вектором дає вектор .

Якщо  і  ,  то .

 

2.         Знайти суму та різницю векторів : 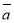(2;1;-2) і 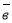( 3;-2;5).

Розв’язання:

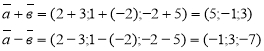
Відповідь:

3.         Знайти модуль суми та різниці векторів :

Розв’язання:

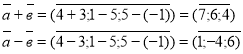
Знайдемо модуль суми і різниці даних векторів за формулою:

Відповідь :

3.Множення вектора на число.

1) Сформулювати означення і закони множення вектора на число. Вказати властивості.

Якщо , то .

Для будь-яких векторів і справедливі рівності:

1) ,де - число;

2),де і - число;

3) , де - число].

2) Помножте вектор

Розв’язання :

Вектор , тому

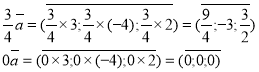
Відповідь :

3).Обчисліть довжину вектора

Розв’язання :

Знайдемо вектори і

Знайдемо суму векторів:

Обчислимо довжину вектора за формулою

Відповідь :

4. Скалярний добуток векторів.

1) Сформулювати означення скалярного добутку двох векторів і кута між двома векторами. Записати формулу.

Кутом між двома ненульовими векторами називають кут між відповідними їм напрямленими відрізками, які виходять з однієї точки.

Скалярним добутком двох векторів називається добуток довжин цих векторів на косинус кута між ними.

Якщо кут між векторами і дорівнює , то їх скалярний добуток

.

Якщо хоч один з векторів або нульовий, то .З цієї формули можна знайти косинус кута між векторами :                            cos.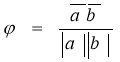

Скалярний добуток векторів і дорівнює .

2) Знайти скалярний добуток векторів : і .

Розв’язання:

Знайдемо скалярний добуток векторів за формулою :

Отже, , а якщо скалярний добуток векторів дорівнює нулю, то вектори не перпендикулярні.

Відповідь : 0.

3)Знайти, косинус кута між векторами і

Розв’язання :

Знайдемо косинус кута між векторами і за формулою :

=

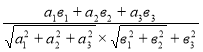
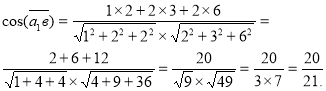
Відповідь:

 

ІІІ. Підсумок гри.

 

За допомогою журі вчитель визначає найбагатших покупців, «оцінює» кожного – учня-покупця і переводить набрані ними бали в 12-бальну шкалу оцінювання.

 

10-12 балів.

Усі відповіді учня подані самостійно, вони повні, логічні. Точні, демонструють глибокі знання з вивченої теми. Учень використовує всі відповідні навички та вміння до розв’язування задач. Аналізує відповіді, робить обґрунтовані висновки.

 

7-9 балів.

Більшість відповідей учня свідчить про глибокі знання з вивченої теми і здатність логічно мислити. Учень достатньо використовує відповідні навички та вміння до розв’язування задач. Аналізує відповіді, робить висновки, враховуючи коментарі вчителя.

 

4-6 балів

Учень знаходить (відбирає) і логічно організовує майже половину даних, що стосуються питання. Використовує далеко не всі навички та вміння до розв’язування задач. Робить неповні висновки.

 

1-3 бали

Учень знаходить мало даних, що стосується питання. Використовує відповідні навички та вміння нечітко і неправильно. Висновки або неточні, або відсутні зовсім.

 

IV. Домашнє завдання:

1.                    Знайдіть довжину діагоналі ВД паралелограма АВСД, якщо А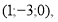В(-2;4;1), С(-3;1;1).
2.                    Доведіть, що трикутник з вершинами А(7;1;-5), В(4;-3;-4), С(1;3;-2) – рівнобедрений.
3.                    Дано точки А(0;1;-1), В(1;-1;2), С(3;1;0), Д(2;1;1). Знайдіть кут між векторами 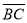і .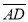

 

ЛІТЕРАТУРА

 

1. Г.П. Бевз, В.Г. Бевз, В.М. Владіміров, Н.Г.Владімірова Геометрія : Підручник для учнів 10-11 класів з поглибленим вивченням математики в середній загальноосвітніх закладах – К: Освіта, 2000.

2.  Роєва Т.Г., Хроленко Н.Ф. Геометрія у таблицях 10-11 класи. Навчальний посібник – Х: Видавнича група «Академія», 2001.

3. Островерхова Н.М. Аналіз уроку : Концепції, методики, технології – К: Інкос, 2003.

4. Пометук О., Пироженко Л. Сучасний урок: Інтерактивні технології навчання. – К: А.С.К., 2004.

ДЛЯ ЗАМІТОК
ДЛЯ ЗАМІТОК
ДЛЯ ЗАМІТОК