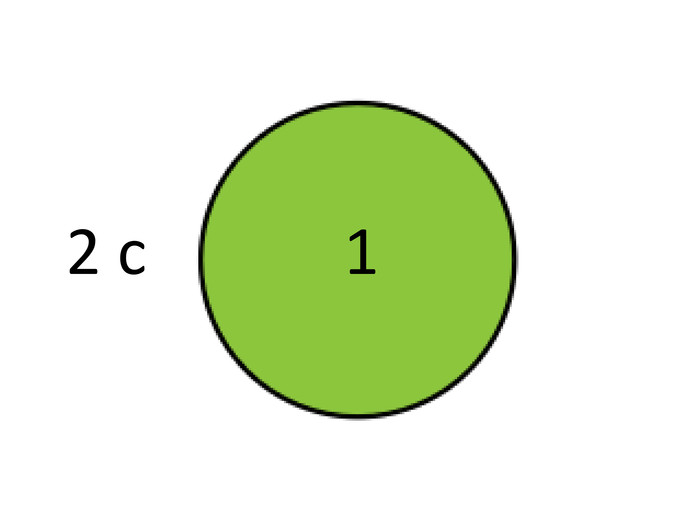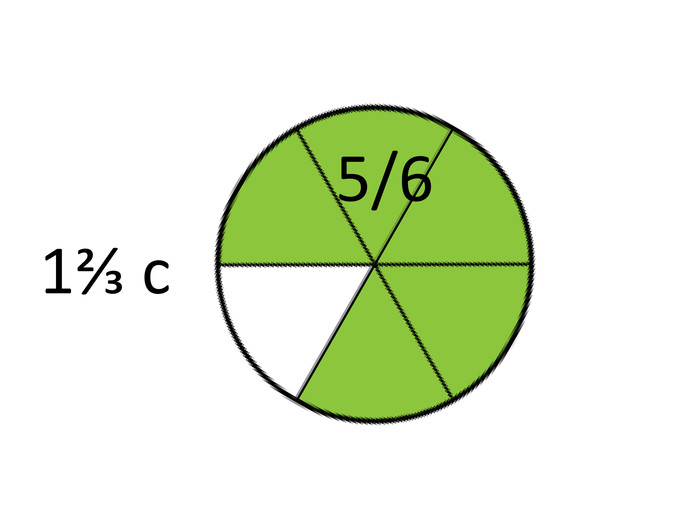Урок "Дроби і музика"

ДРОБИ І МУЗИКА

    Інтегрований урок

6 клас

Мета.

Навчальна: показати учням одне з прикладних застосувань конкретної теми програми, а саме – дробів; в незвичній і цікавій формі закріпити знання учнів в діях над дробами з різними знаменниками.

Розвивальна:  розширити світогляд, пізнавальні інтереси, як, зокрема, до подальшого вивчення математики, так і до мистецтва; показати точки зору видатних людей про важливу роль математики в розвитку музики як сфери інтелектуальної діяльності людини.

Виховна: виховувати почуття прекрасного, любов до української народної пісенної  скарбниці, інтерес до творчості сучасних композиторів на тлі нерозривного зв'язку математики і музики.

Обладнання: магнітна дошка, набір “Долі і дроби”, навчальна таблиця з музичними фрагментами, камертон, метроном, акустична гітара, музичний синтезатор “Ямаха”, мультимедійна дошка, відеопроектор.

Методичні рекомендації. На урок в якості гостів, крім вчителів, запрошуються учні 7 класу, які ще досить близькі до навчальних програм 6 класу, а також за віком. Для створення проблемної ситуації, учні не повинні знати про задум, бо суттєвим для досягнення мети уроку є фактор несподіванки. Урок проводять два вчителі: математики і музики. Все потрібне обладнання попередньо зосереджене на вчительському столі і біля класної дошки, але до пори закрите від очей учнів, а демонструється на відповідних етапах уроку. Учитель музики на початку уроку займає місце серед інших вчителів.

Хід уроку.

І. Організаційна частина.

Учитель математики вітається з класом і гостями. Пропонує  зайняти свої місця. Учням 6 класу для запису в щоденники диктується одночасно із записом на дошці домашнє завдання.   

      В зошити записується дата, вид заняття. Тема уроку ще не оголошується.

ІІ. Актуалізація опорних знань учнів.

 Фронтальне опитування.

1. На які 2 групи можна поділити всі натуральні числа?
2. Число 76 кратне 19. Як сказати це іншими словами?
3. Які ознаки подільності ви знаєте?
4. Що слід зробити, щоб додати 5/18 і 7/12 ?
5. Як знайти спільний знаменник?
6. Основна властивість дробу?
7. Чому не можна ділити на “0” ?
8. За якої умови дріб нескоротний?

(учитель музики виходить і сідає біля прихованого синтезатора)

9.   Несподіване запитання: Що тут робить учитель музики?

ІІІ. Повідомлення теми і мети уроку.

Діти, щоб здогадатися , запишіть тему сьогоднішнього уроку: “Дроби і музика”. [слайд 1]

Саме так, діти, урок у нас буде незвичайним. Адже сьогодні ви довідаєтесь про те, на скільки тісно пов'язані між собою такі, на перший погляд, далекі предмети, як

математика і музика, і саме та математика, яку ви вже вивчили.

І для початку я прочитаю декілька рядків, що належать видатним людям, котрі жили в різні часи, але мали дуже схожі точки зору.

Музика є радість душі, яка обчислює, сама того не усвідомлюючи [XVII]. Г. Лейбніц                                                                               

У музиці чимало подібного до алгебри [XVIII].                                                   Новаліс

Чиста математика в її сучасному розвитку може претендувати на те, що вона найоригінальніший витвір людського генія. Другим претендентом є музика [XVIII ].

                                                                                                                              А. Уайтхед                                                

Музика може бути описаною як математи­ка почуттів, а матемaтика як музика розуму.

[XIX]                                                                                                               Дж.Сільвестр

Людина є дріб. Чисельник це — порівняно з ін­шими — достоїнства людини;  знаменник

•    це оцінка людиною самої себе. Збільшення свого чисельника — своїх достоїнств —

непідвладне лю­дині, але кожний може зменшити свій знамен­ник—свою думку про себе,

 і цим зменшенням наблизитися до довершеності [XIX ].                        Л. М. Толстой

Кого не манить ні краса, ні мистецтво, хто живе вбогим духовним життям, той нічого не

 дасть математи­ці [1927 ].                                                                          М. О. Зарицький

Гра в шахи є начебто насвистування математичних мелодій. [XX].                   Г. Харді                                                                                         

Тим, хто не знає математики, важко збагнути справжню, глибоку красу природи. [1965].                                                      Р. анР.    

Р. Фейнман 

Думаю, вас уже зацікавило вже, де ж ті невидимі ниточки, що пов’язують мистецтво і математику. Отже, зараз спробуємо їх побачити.

Створення проблемної ситуації.

Що це таке, діти? ( на екрані з'являється таблиця з нотною  фразою).    [слайд 2]

А що це? ( на стіл боком, струнами до дітей, ставиться гітара).

А тепер уважно придивіться, де ж тут захована математика?

Не видно? Гаразд. Тоді спробуємо почути. Уважно послухайте , а потім відповісте на мої питання.

• Щоб знайти невідомий від'ємник, треба від зменшуваного відняти різницю.
• У цю ніч чарівну білий сніг хай лежить,

Рік новий по планеті крокує,

І секундная стрілка по колу біжить

Й новорічні секунди рахує.

• (Лунають декілька акордов вальсу)

Діти, скажіть, чим відрізняються 1-й та 2-й тексти? (проза, вірш)

А тепер скажіть, що є спільного між 2-м та 3-м фрагментами? (ритм)

І вірші, і музика обов'язково мають ритм! Пишучи музику, композитор завжди дотримується певного ритму, а допомагає йому в цьому спеціальний прилад – метроном. Ось він. Що ж він показує?  Він відбиває долі секунди, а спеціальна мітка показує кількість ударів за хвилину. Бо кожна мелодія ділиться на такти, які мають певну тривалість.

Та щоб ви краще це уявили, скористаємось уже відомим вам набором “Долі і дроби”.

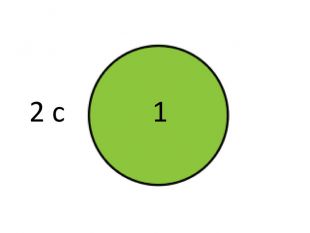
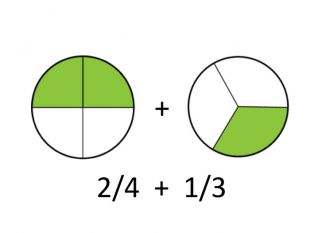
 Перед вами круг.    [слайд 3]                                                               

 Нехай це буде 1 такт, а його тривалість –  2 секунди.

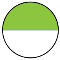
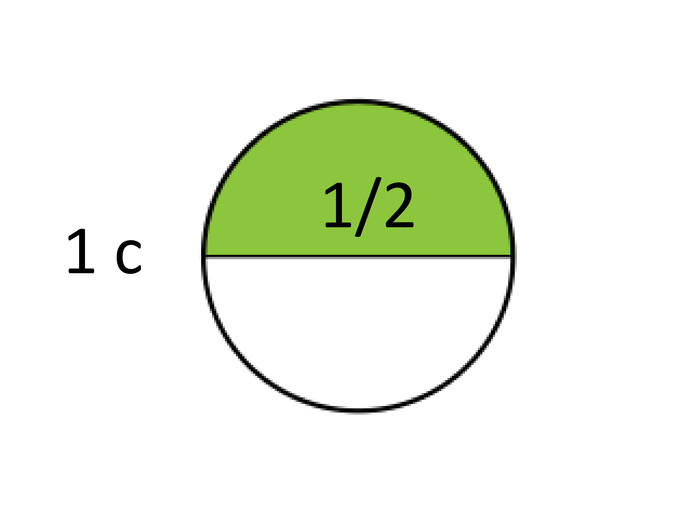
Тоді оце         –    ½ такту, тобто скільки секунд? ( одна)  [слайд 4]

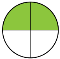
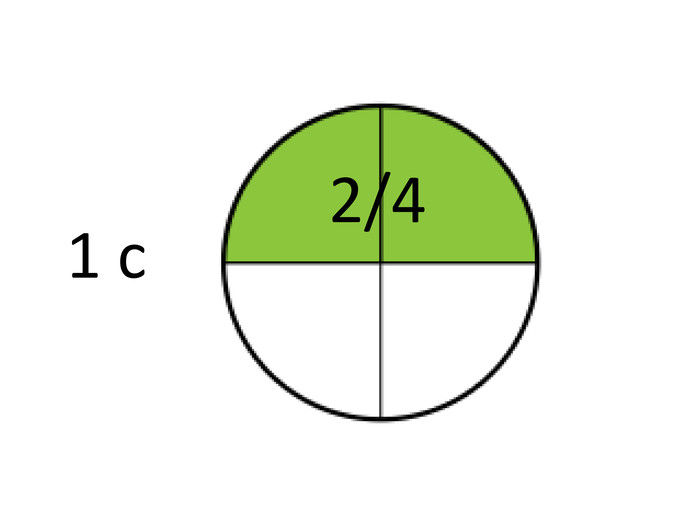
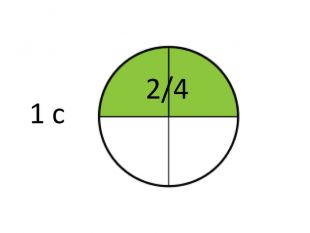
А 2/4 такту        ? ( теж одна секунда)   [слайд 5]

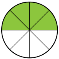
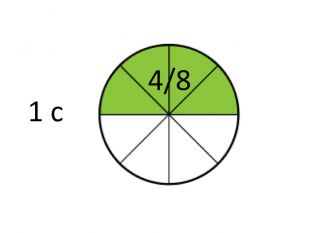
А  також  4/8                [слайд 6] , і  16/32 тощо.

Але коли додавати різні долі одного й того ж такту, можна отримувати різні ритми, а потім – і мелодії.

Наприклад, послухайте, як звучить ритм 2/4 (лунає запис ритму, а потім – перші куплети пісень “Від Києва до Лубен” та “Подоляночка”; діти підспівують).

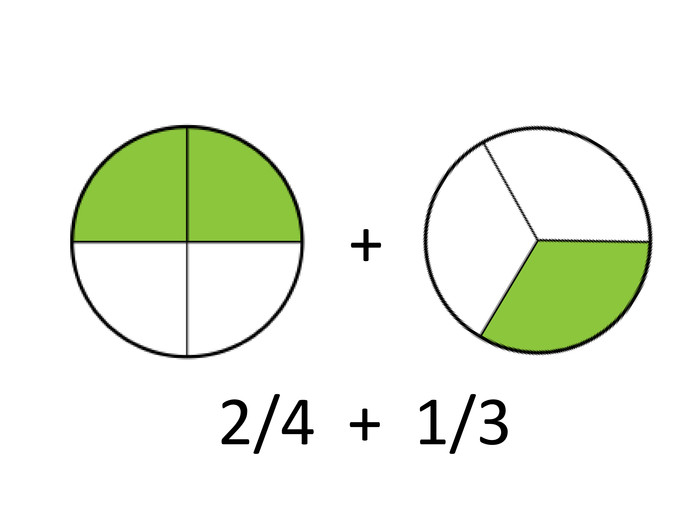
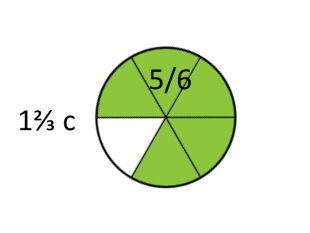
А тепер я до 2/4 прикріплю ще 1/3.   [слайд 7]

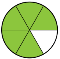
Бачите? Обчисліть, скільки це? Вірно, 5/6.

А як тепер це зазвучить? (лунає новий ритм) Почули різницю? Саме так, додаючи різні долі одного такту, поки не вийде потрібний ритм, музиканти  і створюють  різні мелодії. І в музиці це називається словом “аранжування”.

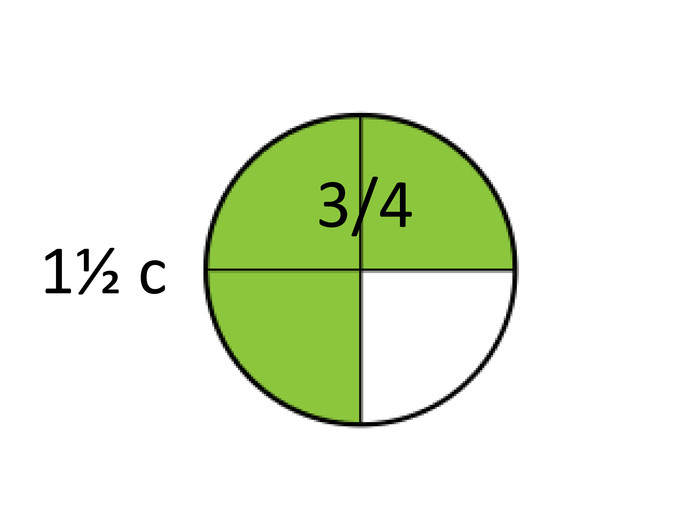
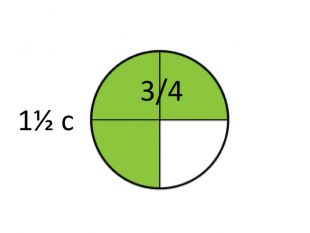
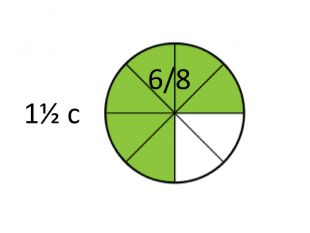
А зараз скажіть, який з дробів більший: 3/4  чи 6/8?

Вірно, вони рівні. В обох випадках це становить який проміжок часу? Подумали.

Так, півтори секунди. [слайд 8]  Але ці півтори секунди набираються   як сума  різних долей секунди, а тому мелодії сильно відрізняються. І зараз Микола Якимович покаже вам це на добре відомих з уроків музики прикладах.

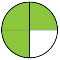
Розмір ¾.               (вчитель математики складає з деталей набору фігуру [слайд 9],  

а вчитель музики награє спочатку “Реве та стогне Дніпр широкий” , а потім “Вишиванку”; діти підспівують)

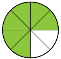
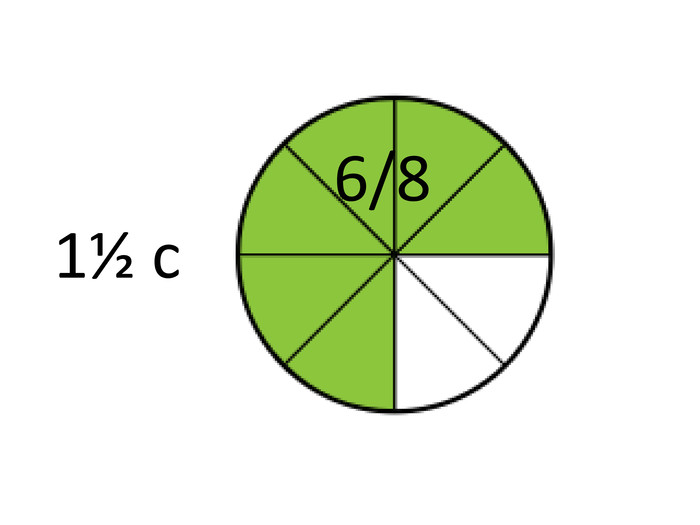
А тепер – розмір 6/8.        [слайд 10] (пропонується “Пісня про вчительку” та

“Чом ти не прийшов”; діти підспівують).

Гарно співаєте. Правда ж, ви і не думали, що скрізь тут дроби? Так де ж вони тут? (вчитель знову повертається до нот і гітари)

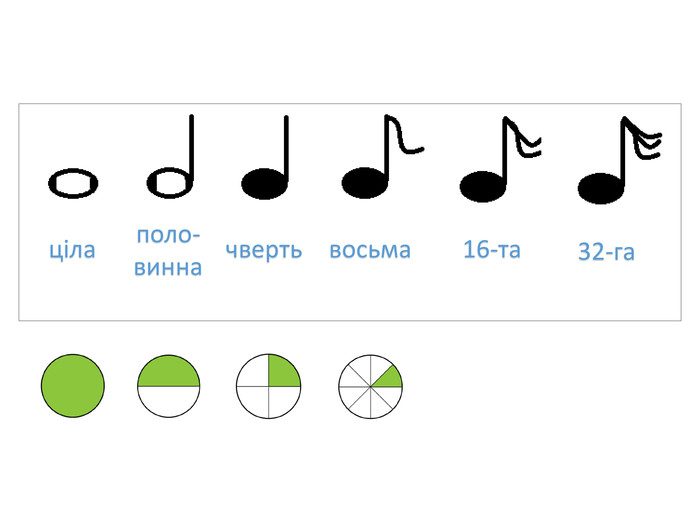
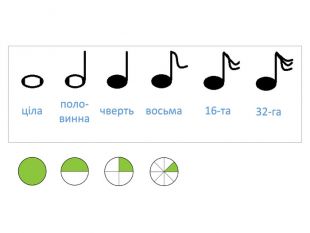
А ось вони, це – нотні знаки. Саме такими значками музиканти вже багато століть позначають дроби, тобто долі секунди. Але вони обходяться без чисельників та знаменників, бо всі нотні знаки – дроби з чисельником 1, а щоб легше впізнати долю секунди, але при цьому обійтися без знаменників [слайд 11],  1 с позначають   ○ , ½ с  -   ● , ¼ с  -   , 1/8 с - ♪ і т.д. А щоб впізнати, який звук у кожної ноти, їх розміщують, як на поличках, на нотному стані. 

  Наприклад, отак звучить нота “ля”(учитель математики ставить ящик камертона отвором на зошит і ударяє молоточком по камертону; звук чути, але слабо). А створив я її спеціальним інструментом – камертоном. А тепер я зроблю те саме , але ось так ( тепер ящик камертона повернутий до класу, лунає сильний звук). Діти, ви почули різницю? В чому ж тут справа? Секрет підсилення звуку – в резонаторному ящику, який підсилює звук, бо розміри його розраховані спеціально для цього. Знову – математика. І резонаторний ящик є у кожного музичного інструмента, і ця гітара – один з прикладів. Трішки пізніше Микола Якимович розповість вам про неї.

  До речі, діти, саме камертонами з нотою “ля” користуються для настройки музичних інструментів. Коли у рояля або скрипки настроєна точно нота “ля”, решту струн натягують так, щоб решта звукоряду не порушувалася. А розміщують ноту “ля” на нотному стані ось тут.

 Діти, а які ноти ви ще знаєте? (діти називають нотний ряд) Так от, щоб, наприклад, зіграти якусь мелодію на гітарі, виконавець повинен знати, яку струну і в якому місці притиснути до грифа і отримати потрібні ноти. Тому дроби заховані і ось тут, бо , якщо ви помітили, гриф не просто поділений на частини; ці частини ще й не рівні між собою

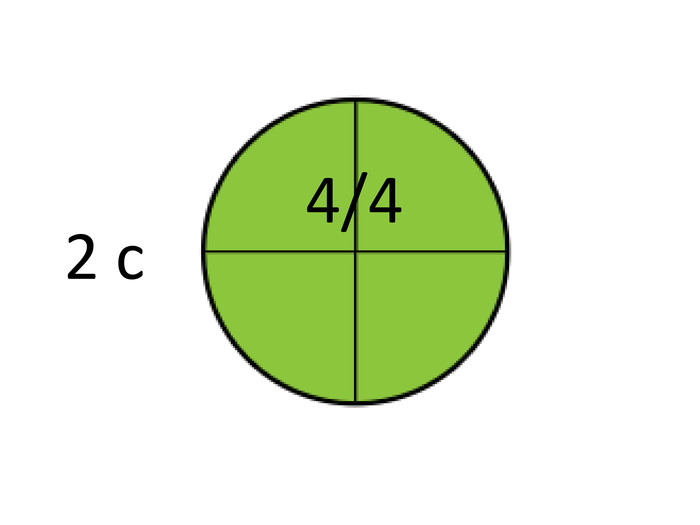
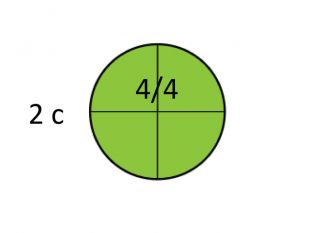
 Скажіть, дітки, а чому дорівнює дріб 4/4 ? Так, одиниці. І зараз ми почуємо, як такий

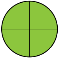
розмір ( доповнює ¾ до 1)        звучить в піснях. [слайд 12]

Пісні, яку ви зараз почуєте, понад 50 років. Я знаю це, бо перейшовши до 2 класу, у 1968 році почав відвідувати заняття шкільного хору. Цю пісню вже тоді співали старшокласниці (лунає “Наша школьная страна”; потім – “Їхав козак містом”; діти підспівують.  Після цього учитель музики стисло розповідає  про особливості будови гітари і гри на ній, запрошує бажаючих навчитися грі на гітарі на  заняття гуртка)

А зараз проведемо невелику музичну вікторину. Всі уривки, що ви почуєте, мають розмір 4/4 і добре вам відомі, бо всі вони зараз у всіх, як то кажуть, на слуху. Вам же треба буде за декількома акордами їх відгадати.(проводиться вікторина;  добірка мелодій, що лунає, може бути різною в залежності від уподобань музиканта, що її складав)

Заключна частина.

Діти! Люди світу розмовляють сотнями мов і тисячами діалектів.

Але всім, хто вивчає математику, зрозуміло, що означає речення  (a+b)c=ac+bc .

І всім, хто вивчає музику, зрозуміло, що означає музична фраза

[слайд 13]

Тобто і мова математики, і мова музики – інтернаціональні! Для них не існує кордонів і не потрібні словники. І тому найрозумніші люди, як ви пам'ятаєте з початку уроку, ставили математику і музику в один ряд як найвищі надбання людського генію.

 На завершення ми пропонуємо вам прекрасну пісню, аранжування якої таке ж багате, як і музична культура народу країни, про яку ця пісня складена. (лунає повний варіант пісні  Т. Петриненка “Україна”)

 V.Підсумок уроку.

Отже , діти, сьогодні ви наочно переконалися, як тісно переплелися дві, на перший погляд, такі далекі сфери людської діяльності, як математика і музика. Когось цей урок, сподіваюсь, спонукає до глибшого вивчення математики. У когось, можливо, виникне бажання навчитися грі на якомусь музичному інструменті. І одне, й інше буде добре. Але майте на увазі, що , навчаючись ще тільки в 6-му класі, ви   не можете навіть уявити , як глибоко проникає математика в усі галузі людської діяльності. Не даремно математику називають мовою всіх наук. То ж вивчайте її, в майбутньому ця наука вам обов'язково знадобиться.

Дякую всім за увагу. На все добре.