урок "Формули коренів квадратног рівняння"

Тема:  Формула коренів квадратного рівняння.

Мета:  Навчальна: домогтися засвоєння формули коренів квадратного      рівняння; сформувати вміння розв’язувати квадратні рівняння за допомогою цієї формули;

           Розвивальна: розвивати розумову діяльність;

          Виховна: виховувати самостійність, намагатися скласти ситуацію успіху для кожного учня.

Тип уроку: засвоєння нових знань, умінь, навичок.

                                                  Хід уроку.

1.  Організаційний момент.  

     (’’ Картки настрою ’’, учні піднімають картку, яка відповідає їх настрою).

         

 

 

2. Перевірка домашнього завдання.

Встановити відповідність : рівняння –відповідь(приклади з домашнього завдання) учні розшифровують закодоване слово «рівняння»

3.   Актуалізація   опорних   знань. Гра «Математичний футбол» учні задають запитання один одному

Приклади питань

-  Які    рівняння    називаються   квадратними?   Наведіть  приклади.

-  Як    називаються    коефіцієнти    квадратного   рівняння

                ах² + bх +с =0?

- Які   квадратні   рівняння   називаються   неповними?    Наведіть  приклади.

-  Скільки   коренів   мають   неповні   квадратні   рівняння   кожного  виду?

Повторити схему складену на попередньому уроці.

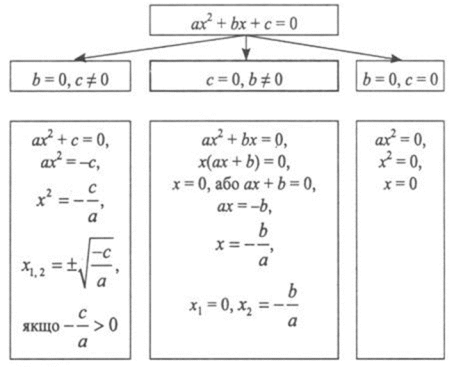
    2)   Гра  ’’  Поспішай   та   не  помились’’.

   На екрані комп’ютера з’являються завдання.

1. Подайте у вигляді подвоєного добутку:                     а) 6х;    б) –0,8у;    в) bх;    г) 11х; 2.  Розкласти на множники                     4х² + 20х + 25; х2 – 21х + 108.

3.  Виділіть   квадрат   двочлена:

 х² + 6х + 8;   х² + 10х +16;  4х² + 20х + 31;  х² – 21х + 108.

4. Назвати коефіцієнти квадратного рівняння :

       а) 2x² + x + 3 = 0;   б) 2x² – x + 3 = 0;  в) 3x² - 6x+ 3 = 0 . 

Підвести підсумок виконання завдання.

4.  Мотивація   навчальної  діяльності.

Учитель. Розлянемо приклад. Нехай тіло рухається прямолінійно вздовж осі х із прискоренням а_х . Якщо у початковий момент часу воно мало швидкість V_0х і перебувало в точці з координатою х₀ , та координату х тіла у момент часу t  можна знайти за формулою

                    Х= 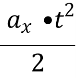+ V_0х t + х₀

Чи є ця формула функцією? Що є незалежною змінною(аргументом)? Чи можна цю залежність назвати квадратичною?

• Розв'яжіть задачі (на партах учнів розкладено аркуші з задачами)

Задача 1. Тіло кинули вертикально вгору з початковою швидкістю 40 м/с. Через який час тіло буде на висоті 60 м? (розвязання задачі висвітлюється на екран)

Дана задача взята з курсу фізики. За формулою залежності переміщення від часу складено (g=9.8m/кв.сек) рівняння:

60 = 40t - 5 t²

Учитель. Чи  можна це рівняння вважати квадратним? Що є змінною? Але  ця задача  буде вами розвязуватися в курсі фізики в 10 класі.

Задача 2. Господарі вирішили огородити ділянку перед фасадом будинку, що прилягає до стіни. Довжина використаної сітки становила 42 м, а площа ділянки, яку огородили, — 216 м². Яка довжина й ширина ділянки?

(Учні класу працюють у парах. Розв 'язування задачі перевіряється учнями за готовими записами на дошці.)

Якщо довжину ділянки позначити за х, то ширина ділянки 42-2х. Оскільки площа 216 м², то складаємо рівняння: х(42-2х)=216.

Отримали рівняння 42х-2х²=216.

Учитель. Таке рівняння ми не розв'язували. Це новий тип рівнянь, які називаються повними квадратними. Ми вже навчилися розв’язувати неповні квадратні рівняння, але ви знаєте, що існують ще й повні квадратні рівняння.  (З метою створення відповідної мотивації пропоную учням розв'язати дане  рівняння: виділенням повного квадрата, способом групування.) Учні розбито на три групи. Кожна група розв'язує дане рівняння відомими їм способами: виділення квадрата двочлена та способом групування.

Учитель. Чи легко розвязувати дане рівняння цими способами?

Чи існує інший спосіб для розвязування таких рівнянь?

Аналіз ситуації, що склалась, приводить до формулювання проблеми: необхідно знайти єдиний достатньо простий алгоритм розв'язання квадратних рівнянь загального вигляду. Розв'язання цієї проблеми і є головною метою уроку.

Їх зазвичай розв’язують за формулою, яку можна також використовувати і для неповних квадратних рівнянь, а також для рівнянь з параметрами.

Історичне повідомлення (учням було задане завдання)

Розв’язуванню квадратних рівнянь присвятив свої праці відомий український математик, професор Микола Чайковський (1887–1970). Він протягом тривалого часу працював у вищих навчальних закладах Львова, Одеси, Кам’янця-Подільського. М.Чайковський зробив вагомий внесок у створення української математичної термінології, а також брав активну участь у виданні українських підручників з математики. Застосування  основних   властивостей    значно   полегшує   розв’язання   багатьох   рівнянь.  Отже,  сьогодні   на   уроці   ми  з  вами  вивчимо   формулу    коренів   квадратного   рівняння.

Оголошення    теми  і  мети  уроку.

5.  Вивчення   нового  матеріалу. Виведення формули коренів квадратного рівняння.

       1. Виведемо формулу коренів квадратного рівняння ах² + bх + с = 0.

Помножимо обидві частини рівняння на 4а (а ≠ 0), матимемо:

4а²х² + 4аbх + 4ас = 0,

(2ах)² + 2∙2ах∙b + b² – b² + 4ас = 0,

(2ах + b)² – b² + 4ас = 0,

(2ах + b)² = b² – 4ас.

Робота з підручником : знайти невідоме слово.

      Вираз  b² – 4ас називають дискримінантом (від латинського diskriminns – той, що розрізняє) даного рівняння і позначають буквою D. Тоді  (2ах + b)² = D.

Постановка проблеми №2

Учням  пропонуються декілька рівнянь.

 2x²+x+3=0 і 2x²–x+3=0;
2x²-x–3=0 і 2x²+x–3=0;
3x² - 6x+ 3 = 0  і  3x² + 6x + 3 = 0.

• Які з наступних рівнянь, на ваш погляд, мають корені, а які - не мають коренів?
• Чи можете ви відповісти на це питання, не розв’язуючи рівнянь?
•  Як ви думаєте, кількість коренів квадратного рівняння визначається:
            -одним коефіцієнтом;
            -двома коефіцієнтами;
            -трьома коефіцієнтами?
   

Гіпотези учнів.

Робота з підручником.

1. Встановимо залежність коренів рівняння від дискримінанта.

Вчитель створює проблемну ситуацію, запропонувавши учням відповісти на запитання:  – Скільки коренів може мати рівняння (2ах + b)² = D і від чого це буде залежати? (Якщо учні не можуть знайти правильної відповіді, то вчитель пропонує назвати кількість коренів рівняння виду х² = а. Аналізуючи разом з учнями їхні відповіді робиться висновок про кількість коренів повного квадратного рівняння. )

Так, ви праві, число коренів квадратного рівняння ax²+ bx+ c = 0 залежить від виразу, складеного з коефіцієнтів цього рівняння.

• Що це за вираз?
• Як він впливає на кількість коренів?
• Проаналізуємо формулу коренів квадратного рівняння.

 

                               
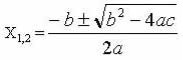
1. Якщо b² - 4ac >0, то квадратне рівняння має два різні дійсні корені.
2. Якщо b² - 4ac =0, то квадратне рівняння має два однакові дійсні корені.
3. Якщо b² - 4ac <0, то квадратне рівняння не має дійсних коренів.

Що спільного між поняттям «світлофор» і «дискримінант»?

(діти відповідають і відповідно позначають кольорами у   своїй блок-схемі)

ах2+ bх + с = 0, а ≠ 0 – загальний вигляд квадратного рівняння
D = b2 - 4ас
D < 0	D = 0	D > 0
Коренів немає	х = –	х1=,                                                               х2=.

 

 

 

 

 

 

 

Підсумок : отже, ми отримали формули, які називають формулами квадратного рівняння,користуючись якими ми можемо розвязувати будь які квадратні рівняння.

 

Щоб рівняння розв’язати,

Треба формули всім знати.

Ще й знайти дискримінант –

Не ховайте свій талант.

                                                  Якщо D у вас додатний,

То два розв’язки знайдеш.

Зможеш точно розв’язати,

    Шляхом правильним підеш.

Якщо нуль – усе простіше:

Один корінь шукай швидше.

  А якщо дискримінант

  Має ще від’ємний знак,

  То роботі вже кінець –

  Зовсім розв’язків немає.

  А ти – учень-молодець.

 

А тепер,  діти, допоможіть скласти ще один алгоритм розв’язання  квадратного рівняння.

(Діти самі складають алгоритм)

 Після цього на  екрані відкривається таблиця із заздалегідь складеним учителем алгоритмом, і діти звіряють власний варіант з істинним.

                                                     АЛГОРИТМ
   1.  Виділити в квадратному рівнянні коефіцієнти.
   2.  Обчислити дискримінант D.
   3. -  Якщо D<0, те рівняння не має дійсних коренів.
       -  Якщо D>чи=0, то обчислити корені по формулі.
   Розглянемо   приклад.

     а) 3х² - 5х +2 =0;

       а = 3,    b = -5,   с = 2;

       D = (-5)² – 4*3*2 = 25 – 24 = 1;

       D = 1>0 – рівняння має 2 різні корені.

       х =   = ;          х₁ = 1;             х₂ = .

6.   Закріплення    нових   знань  і  вмінь.

 (Учні працюють в групах.  Групи   гетерогенні,   тобто   об’єднані   сильні,   середні   і   слабкі   учні.   Учитель   контролює   роботу. Це   необхідно    для   стимулювання    творчого   мислення   й   інтенсивного  обміну   ідеями).

1. Скільки коренів має рівняння?

 1.  х²-9х+14=0?   2.   х²-8х+15=0?

 

    А) два;     Б) один;                              А) два;       Б) один;

    В) не має коренів;                    В) не має коренів;

    Г)  безліч.                     Г)  безліч.

 

 3.   2х²+х+2=0?   4.    Зх²+х+4=0?

    А)  два;    Б) один;                    А) два;         Б) один;

    В)  не має коренів;                    В) не має коренів ;

    Г)   безліч.                              Г)  безліч.

 

2.  Розв’яжіть   квадратне   рівняння   за   допомогою   формул коренів квадратного рівняння.

                                 Картка – інформатор

                                   Розв’язати рівняння:

              а)  2х² + 3х – 5 = 0                              b)   5х² - 7х + 2 = 0                                                                  

1. Виділити коефіцієнти:  

1.      а = … ;      в = … ;      с = …                1.  а = … ;      в = … ;      с = …

2. Знайти дискримінант:

     D = 3² – 4 …                                                      2.  D = 49 - …

3. Знайти корені рівняння
                   х_1,2 =                                                         х_1,2 =                                   

                   х_1,2 =                                                                х_1,2 =

                 х₁ =                                                                      х₁ =

                 х₂ =                                                                      х₂ =

• Для дітей з достатнім рівнем знань( на вибір):

Розв’язати рівняння:

1.  3х² + 8х – 3 = 0 ;

2. - х² + 2х + 8 = 0;

3.   х² - 6х  = 4х – 25;

4. (5х – 4)(х + 8) = 0.     

Розвязані рівняння учні здають учителю для моніторингу засвоєння знань нового матеріалу.  

Учитель.  А тепер повернемося до першої задачі.

60 = 40t - 5 t²

• Якого виду складено рівняння?
• Назвіть коефіцієнти рівняння.
• За допомогою складеного алгоритму розв'язування повного квадратного рівняння розв'яжіть його.

-5t² +40 t - 60 = 0

 t² - 8 t + 12 = 0.

 t₁ = 2; t₂ = 6.

Розв'язки даного рівняння свідчать про те,що ми побачили з точки.

Тіло опинилося на висоті 60 м два рази: через 2 с і через 6 сек після кидання вертикального вгору.

9.   Підсумок   уроку.(Робота в парах)

Учням видаються 2 картки різного кольору. На одній з них закодовані початки означень, які пронумеровані від 1 до 12. На другій – продовження цих означень, які закодовані буквами. Учні зв’язують початок і кінець фрази в одне речення, при цьому встановлюють відповідність між цифрами і буквами. В разі, якщо вони зробили все правильно, отримують закодоване слово «ДИСКРИМІНАНТ». Отже, прочитайте закодоване слово і назвіть формулу дискримінанта:

(Діти, які сидять за першими партами читають: дискримінант...,і називають формулу дискримінанта )

Картки-завдання

1.	Рівняння виду ах2 + bх + с = 0, де х – змінна, а а, b, с – дані числа, причому а ≠ 0 ...	К	рівнянню х2 = 0
2.	Числа а, b, с –...	Н	називають першим коефіцієнт-том
3.	Неповні квадратні рівняння бувають таких видів ...	И	повними і неповними
4.	Рівняння виду ах2=0 рівно-сильне ...	І	рівносильне рівнянню х(ах + b) = 0
5.	Один із способів розв’язування квадратних рівнянь ...	Д	називаються квадратними
6.	Квадратні рівняння бувають ...	Т	якщо D < 0
7.	Квадратні рівняння можна розв’язувати ...	Н	два корені, один корінь
8.	Рівняння виду ах2 + bх = 0 ...	И	коефіцієнтами квадратного рів-няння
9.	Число b в квадратному рівнянні ...	Р	це спосіб виділення квадрата двочлена
10.	Другим коефіцієнтом квадрат-ного рівняння ...	М	за допомогою формул
11.	Повне квадратне рівняння може мати ...	А	називається число b
12.	Квадратне рівняння не має розв’язків ...	С	ах2= 0, ах2 + bх = 0, ах2 + с = 0

 

Прес – конференція.

Обговорення  того,  наскільки   повно   було   виконано   роботу,  в  якому   напрямку   необхідно  працювати   далі.

 (’’ Картки настрою ’’, учні піднімають картку, яка відповідає їх настрою на кінці уроку. Порівнюють, яка картка була піднята на початку уроку, а яка по закінченню).

Виставлення оцінок активним учням

Домашнє завдання  : міні-проект «Застосування квадратних рівнянь в інших сферах наук», за підручником( різнорівневе)

Література.

1. Бевз Г.П. Алгебра : підручник для 8 класу загальноосвітніх навчальних закладів/ Г.П. Бевз,В.Г.Бевз. – К.: Зодіак-ЕКО,2008. – 256с.:іл.
2. Кравчук В.Р. Алгебра.Пробний підручник для 9 класу/ В.Р.Кравчук,М.В Підручна,Г.М. Янченко. За редакцією З.І.Слєпкань.Видання друге,перероблене та доповнене – Тернопіль.: Підручники і посібники, 2004.- 248 с.
3. Мерзляк А.Г. Алгебра.8кл.:збірник задач і контрольних робіт/ А.Г.Мерзляк,В.Б.Полонський,Ю.М.Рабінович,М.С.Якір.- Х.:Гімназія,2010.-96с.:іл.
4. Коршак Є.В. Фізика:10 кл.:підручник для загальноосвітніх навчальних закладів: рівень стандарту/Є.В.Коршак,О.І.Ляшенко,В.Ф.Савченко.-К.:Генеза,2010-192с.:іл.
5. Римкевич А.П. Збірник задач з фізики для 8-10 класів середньої школи/А.П. Римкевич, П.А. Римкевич.-7-е вид.-К.: Рад.шк.,1985.-176с.,іл.
6.  Наказ МОН України від 05.05.08 № 371.
7. Постанова Кабінету Міністрів України від 23.11.2011 № 1392.
8. Електронний ресурс.-[режим доступу]:http://festival.1september.ru/