Стаття "Формування дивергентного мислення учнів основної школи".

Мартиненко О. В.

кандидат фізико-математичних наук,доцент кафедри математики

elenamartova21@gmail.com

Рудик В. В.

учитель інформатики КУ Сумська ЗОШ №23, м. Суми

vladislava_3@mail.ru

ФОРМУВАННЯ ДИВЕРГЕНТНОГО МИСЛЕННЯ УЧНІВ ОСНОВНОЇ ШКОЛИ ПРИ НАВЧАННІ МАТЕМАТИКИ (НА ПРИКЛАДІ ПОБУДОВИ ГРАФІКІВ ФУНКЦІЙ)

Анотація. Мартиненко О. В., Рудик В. В. Формування дивергентного мислення учнів основної школи при навчанні математики (на прикладі побудови графіків функцій).

У статті розглянуто деякі аспекти розвитку дивергентного мислення учнів основної школи при навчанні математики, схарактеризовано принципи, які повинен враховувати учитель при підготовці та проведенні уроків з математики. Авторами описано специфіку формування дивергентного мислення при вивченні та побудові графіків функцій учнями основної школи.

Ключові слова: мислення, дивергентне мислення, конвергентне мислення, графік функції, побудова графіків функцій.

Постановка проблеми. Реформування системи шкільної освіти в Україні зумовлює пошук ефективних методів організації навчального процесу та корекцію методик викладання шкільних предметів. Реалізація творчого потенціалу дітей покоління Z неможлива без розвитку креативності та системності їх мислення, інтелектуальної допитливості, навичок особистісної та групової взаємодії, ІТ-обізнаності, здатності до оригінальності та інновацій. [10]

Математика належить до основних шкільних предметів, при вивченні яких формується та розвивається креативне мислення. Дивергентне мислення є складоваю креативного, воно забезпечує так званий “феномен винахідливості.” На жаль, більшість класичних педагогічних методик сучасної шкільної освіти використовує модель конвергентного мислення, яке є більш лінійним і полягає в поетапному виконанні завдань, дотриманні певного алгоритму та застосуванні елементарних операцій

Завдання, що пропонуються учням, від самого початку передбачають існування правильної відповіді; діти отримують оцінки за швидкість, детальність та точність розв’язування; при письмових відповідях обов’язково враховується акуратність і правильність оформлення. Виконання тестових завдань також ґрунтується на стратегії конвергентного мислення.

Звичайно, конвергентне мислення є дуже важливим, але реальне життя не завжди будується за правилами; досить часто вирішення питань потребує нових ідей, творчого підходу, креативного мислення. Це зумовлює необхідність формування та розвитку дивергентного мислення учнів, як складової творчого, насамперед при навчанні математики в основній школі.

Аналіз актуальних досліджень. Засновником концепції дивергентного мислення вважається видатний психолог Д. Гілфорд, який у 50-х роках двадцятого століття займався вивченням творчого потенціалу особистості. У 1950 році він надав свою наукову теорію Американській психологічній асоціації, яку вдосконалив аж у 1976 році. Саме тоді Д. Гілфорд  назвав дивергентне мислення складовою частиною творчості. У своїх дослідженнях вчений виокремлював дивергентне та конвергентне мислення. Він вважав, що характерним проявом дивергентного мислення є здатність до пошуку та генерування нових інформаційних об’єктів, конвергентного – знаходження цілком конкретних відповідей на цілком визначені питання [2]. Сам термін “конвергентне мислення” походить від латинського слова ”соnvergere”, що означає ”збігатися”. Цей тип мислення є дуже важливим при навчанні учнів, він працює при алгоритмічному підході до виконання завдань, при розв’язуванні тестів.

На практиці знання фактів та алгоритмів не завжди допомагає у вирішенні конкретного завдання, а алгоритмічне мислення гальмує появу креативних ідей. Для того, щоб рухатися вперед, приймати нестандартні рішення, потрібно розвивати в учнів дивергентне мислення.

Термін “дивергентне мислення” у перекладі з латинської (“divergere”) означає “розбігатися”. Особливістю цього типу мислення є те, що при аналізі причин і наслідків певної проблеми відсутній непохитний зв’язок. Це призводить до появи нових комбінацій, нових співвідношень між елементами, а отже з’являється більше шляхів її вирішення.

Дослідження специфіки дивергентного мислення у своїх наукових працях відобразили Е. Торранс, Дж. Гілфорд, К. Тейлор, Г. Грубер, І. Хайн, А. Шнедер, Д. Роджерс. Вони встановили, що цей тип мислення працює на пошук неординарних ідей, на використання нестандартних форм діяльності, на формування дослідницького інтересу. Дивергентність дозволяє людині краще аналізувати і порівнювати факти, будувати гіпотези та висувати припущення, класифікувати отриману інформацію. Саме тому, одним із найважливіших завдань при навчанні математики учнів основної школи є формування та розвиток у них дивергентного мислення.

Мета статті – описати особливості формування та розвитку дивергентного мислення учнів основної школи при навчанні математики (на прикладі побудови графіків функцій).

Виклад основного матеріалу.

Формування та розвиток дивергентного мислення є досить складним завданням, що стоїть перед шкільною освітою. Відомо, що його основою є так звані випадкові ідеї, саме тому люди з геніальним складом розуму можуть погано відповідати на тести IQ, які побудовані за класичною конвергентною схемою. Для оцінки дивергентного інтелекту особистості досить часто застосовують нестандартні методики, які ґрунтуються на таких критеріях:

• швидкості –  кількості ідей, які виникають за одиницю часу;
• оригінальності – умінні мислити творчо, відходити від певних алгоритмів, установлених правил;
• чутливості – здатності швидко переходити від однієї ідеї до іншої, умінні бачити незвичайне в незначних деталях, знаходити протиріччя;
• образності – використанні асоціацій для вираження власних ідей, роботі з символами та образами, пошуку нестандартних елементів у простих міркуваннях і простоти в складних поняттях.

Українські науковці також дотримуються думки, що дивергентне мислення є більш інтуїтивним, на відміну від конвергентного – логічного та послідовного. Воно передбачає, що на будь-яке поставлене питання існує не одна, а декілька правильних відповідей [1, c. 70].

До особливостей дивергентного мислення відносять такі:

• дивергентне мислення являє собою вищий рівень розвитку наочно-образного мислення;
• процес дивергентного мислення здійснюється від конкретного через абстрактне до нового конкретного (уявного) образу;
• дивергентне мислення проявляється у розумінні кінцевого результату роботи ще до її початку.

До показників дивергентного мислення також відносять гнучкість.

Саме завдяки дивергентному мисленню народжуються креативні, оригінальні ідеї.

На сьогоднішній день існуюча система шкільної освіти не забезпечує повною мірою розвиток у учнів дивергентного мислення при навчанні математики, тому саме його формування є одним з основних завдань, що стоять перед учителем. Для успішного вирішення цієї проблеми при підготовці та проведенні уроків з математики вчитель повинен враховувати такі принципи:

•            відкритості завдань, коли вправи мають не один, а декілька варіантів розв’язування;
•            використання різних методів та форм отримання та подання необхідної інформації;
•            розвиток пізнавальної активності в цілому, що виражається у наданні учням можливості активно висувати гіпотези, ставити запитання та проводити дискусії;
•            допомога дітям у вираженні власних ідей, їх аналізі; недопущення їх незадовільної оцінки;
•            використання особистого прикладу творчого підходу до розв’язування проблем;
•            заохочення самостійного пошуку розв’язування завдань;
•            використання сучасних інформаційно-комунікаційних технологій (комп’ютера, мультимедійного проектора, інтерактивної дошки, Інтернету, програмного забезпечення). [9]

Правильний вибір та поєднання зазначених принципів, відповідно до теми уроку або завдання, є одним із чинників, які забезпечують досягнення максимальних результатів при навчанні учнів.

До найбільш ефективних форм навчальної діяльності щодо розвитку дивергентного мислення учнів на уроках математики, на наш погляд, можна віднести: ситуативне моделювання, опрацювання дискусійних питань, метод проектів, проблемне викладання, задачі практичного змісту, особистісно-орієнтоване навчання.

У процесі формування дивергентного мислення учнів на уроках математики важливою формою роботи є, зокрема, розв’язування так званих дивергентних завдань. Під дивергентними завданнями ми будемо розуміти такі, що відповідають хоча б одній із даних вимог:

1. Умова задачі містить надлишкові дані. Учень має можливість комбінувати дані та виокремлювати певний комплекс умов, а також обирати найбільш доцільний для себе варіант розв’язання задачі.
2. В умові задачі недостатньо даних для її розв’язання або деякі дані задані в неявному вигляді. Учню необхідно здійснити пошук відсутніх даних, вибрати, співставити їх з позначеними в умові математичними величинами, визначати потрібний для розв’язування задачі комплекс величин.
3. Можливий комбінований варіант умови, тобто для визначення шуканого в умові задані надлишкові дані, але вони не використовуються при розв’язуванні або можуть направляти по хибному шляху. Водночас, у ній не вистачає потрібних для отримання розв’язку величин, їх учень повинен відшукати самостійно.
4. Задача допускає не один спосіб (мінімум два) розв’язування: графічний та аналітичний, дедуктивний та індуктивний, аналітичний та синтетичний тощо. Виходячи з умови конкретної задачі та досвіду роботи з подібними завданнями, учень знаходить свій спосіб розв’язування. При декількох варіантах розв’язування він визначає найбільш раціональний.

Незважаючи на те, що задача має тільки одну правильну відповідь, її можна віднести до задач дивергентного типу, оскільки існує декілька способів розв’язування.

5. Задача має декілька правильних відповідей. Зазвичай, з такими задачами в учнів виникають труднощі, вони можуть вказувати не всі відповіді. Складність для учнів полягає в тому, щоб знайти всі можливі варіанти відповідей.
6. Задача містить можливість переформулювання її умови, змінення запропонованого змісту, при цьому, початкові дані та шукані величини зберігаються. Це стимулює мисленеву діяльність учнів по пошуку шляхів розв’язування задачі та використання незвичних аналогій тощо. [4, c. 28 – 29]

Очевидно, що чим більше вимог задовольняє умова задачі, тим складніше вона розв’язується, але, водночас, має більший потенціал для розвитку дивергентного мислення школярів при навчанні математики.

Однією з найважливіших тем, що вивчається в шкільному курсі алгебри є графіки функцій, вони супроводжують людину протягом усього життя. Аналіз властивостей функції та вибір відповідного алгоритму побудови її графіка, відтворення властивостей функції за відомим графіком є саме тим навчальним матеріалом, що сприяє розвитку дивергентного мислення учнів.

Провідне місце у курсі алгебри 9 класу займає тема «Квадратична функція». Властивості квадратичної функції використовуються під час розв’язування широкого кола задач, рівнянь, нерівностей, застосування їх в курсі геометрії тощо. В арсеналі шкільної математики накопичено велику кількість задач, розв’язування яких ґрунтується на властивостях квадратичної функції. Це стосується задач як алгоритмічного характеру, так і дослідницького, провідну роль серед останніх займають задачі з параметрами. Значну увагу слід приділяти встановленню відповідності між властивостями квадратичної функції та її графічним зображенням. Вагомим елементом математичної культури є застосування графічних методів та інтерпретацій у розв’язуванні задач з параметрами [8, c. 9].

До дивергентних завдань, які розглядаються в цій темі, у класах з поглибленим вивченням математики, можна віднести завдання на побудову графіків функцій, що включають цілу або уявну частину.

Розглянемо приклади таких графіків функцій.

Будуємо графік функції , вершина (0;0); вітки вгору. Проведемо прямі y = n (n є Z).

Точки перетину графіків y = n (n є Z) та належать графіку . Спроектуємо частини графіка , що лежать між прямими y = n та y = n+1, n є Z на пряму. Одержимо графік .

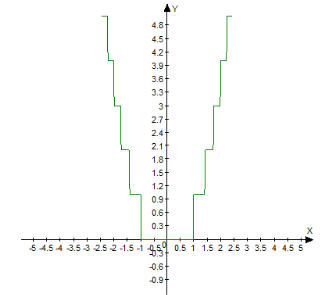
Рисунок 1. Графічна інтерпретація графіка функції

Будуємо графік функції , вершина (0;0); вітки вгору. Проведемо прямі x = n (n є Z).

Точки перетину графіків x = n (n є Z) та належать графіку , бо їх абсциси цілі числа. Спроектуємо частини графіка , що лежать між прямими x = n та x = n+1, n є Z на пряму. Одержимо графік .

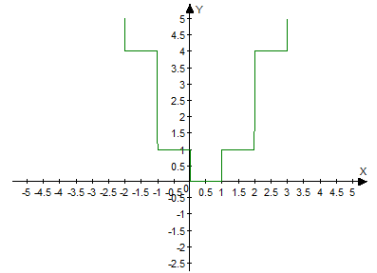
Рисунок 2. Графічна інтерпретація графіка функції

Будуємо графік функції на проміжку , а потім будуємо такий самий графік на кожному з проміжків, .

Одержимо графік .

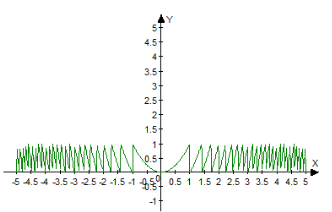
Рисунок 3. Графічна інтерпретація графіка функції

Вказані завдання доречно застосовувати для відпрацювання вмінь: розпізнавати квадратичну функцію серед інших елементарних функцій; знаходити координати вершини та напряму віток параболи;  закріпити вміння аналітично досліджувати властивості квадратичної функції, а також схеми виконання основних видів геометричних перетворень графіків функцій. Розвивати творчо-пошукову діяльність, обчислювальні навички, графічну культуру, мислення, пам’ять, кмітливість, увагу, ініціативність, самостійність; виховувати навички колективної роботи та співпраці, формувати пізнавальний інтерес.

На жаль, на сьогоднішній день, дивергентні задачі майже відсутні у збірниках, підручниках з математики. Задачі у шкільних підручниках за своїм змістом конкретні, відрізняються чітко визначеними умовами та вимогами і, зазвичай, припускають однозначність розв’язку з однією відповіддю.

Суть більшості завдань полягає не в тому, щоб знайти правильну числову відповідь, а в тому, щоб знайти шляхи, способи, алгоритми розв’язання завдань. У цьому випадку, з точки зору мислення, відповіддю є способи розв’язання проблеми. Якщо ж при цьому учень бачить декілька варіантів розв’язання, то можна, з впевненістю, стверджувати, що активізувалося дивергентне мислення.

Отже, можна з впевненістю стверджувати, що дивергентні задачі вимагають більш відкритого типу мислення, стимулюють в учнів розвиток уміння бачити проблему з різних ракурсів, знаходити нові нестандартні підходи, мислити не шаблонно. При розв’язуванні дивергентних задач на уроках математики учень оцінює інформацію з різних точок зору, а також конкретизує, доповнює, розвиває, систематизує, комбінує її. Досить важливим підходом до розв’язування дивергентних задач є дослідження їх варіативності, що дає змогу виявити учнів, які відзначаються самостійним мисленням, а також тих, які мають прогалини в знаннях, або не звикли до творчого пошуку, мислять стереотипно, шаблонно.

ЛІТЕРАТУРА

1.      Вдовенко В. В. Використання дивергентних задач на уроках математики як необхідна умова розвитку творчої особистості учня / В. В. Вдовенко // Акутальні питання природничо – математичної освіти: збірник наукових праць / Міністерство освіти і науки України, Сумський державний педагогічний університет імені А. С. Макаренка. – Суми: ВВП «Мрія», 2013. – № 1. – С. 69 – 73.
2.      Волобуєва Т.Б. Розвиток творчої компетентності школярів / Т. Б. Волобуєва // Харків: Основа, 2005 – 168 с.
3.      Гілфорд Дж. Три сторони інтелекту // Психологія мислення. М.: Прогрес, 1965 –14 с.
4.      Дегтярев С. Н.  Учебно – познавательный процесс в аспекте развития дивергентного и конвергентного мышления / С. Н. Дегтярев // Обазование и наука. – 2009. – № 4 (61). С. 23 – 36. 
5.      Мерзляк А. Г. Алгебра: підруч. для 7 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2015. – 256 с.
6.      Мерзляк А. Г. Алгебра: підруч. для 8 кл. з поглибленим вивченням математики / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2016. – 384 с.
7.      Мерзляк А. Г. Алгебра для загальноосвітніх навчальних закладів з поглибленим вивченням математики: підруч. для 9 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2017. – 416 с.
8.      Навчальна програма для поглибленого вивчення математики в 8-9 класах загальноосвітніх навчальних закладів [Електронний ресурс] – Режим доступу до ресурсу: https://mon.gov.ua/storage/app/media/zagalna%20serednya/programy-5-9-klas/matematika-algebra-geometriya.pdf
9.      Нова українська школа: порадник для вчителя / Під заг. ред. Бібік Н. М. – К.: ТОВ «Видавничий дім «Плеяди», 2017. – 206 с.
10. Подкопаєва Е. В. Шляхи розвитку творчої особистості учня. Педагогіка співтворчості та співробітництва [Електронний ресурс] / Еліна Вікторівна Подкопаєва – Режим доступу до ресурсу: http://osvita.ua/school/lessons_summary/edu_technology/27669/.

Summary. Martynenko O.V., Rudyk V.V. Formation of divergent thinking of primary school pupils in mathematics education (on the example of plotting functions).

In the article some aspects of the development of divergent thinking of primary school students during mathematics studies are considered, the principles which teachers should take into account when preparing and conducting mathematics lessons are given. The authors describe the specifics of the formation of divergent thinking in studying and constructing graphs of functions by pupils of the main school.

Keywords: thinking, divergent thinking, convergent thinking, function graph, plotting functions.