Урок геометрії . 9 клас. Тема " Роз'вязування трикутників"

Урок геометрії    9 клас

Тема: Розв’язування трикутників

Мета:  Формувати вміння і навички розв’язування трикутників за трьома його елементами; повторити теореми косинусів, синусів та наслідки з них; повторити типи задач на обчислення елементів довільних трикутників; показати практичну спрямованість математичних знань; навчити застосовувати знання для розв’язування практичних задач; формувати полікультурну компетентність через використання інформації з історії математичних відкриттів;

розвивати  пошукову пізнавальну активність учнів, уяву, логічне мислення, зв’язне мовлення, вміння аналізувати, робити висновки;

 виховувати наполегливість, впевненість в собі, інтерес до математики

                                                    План уроку

1. Організаційний момент
2. Повідомлення теми та мети уроку
3. Мотивація навчальної діяльності
4. Актуалізація опорних знань
5. Узагальнення та систематизація знань учнів
6. Закріплення вмінь і навичок
7. Підсумок уроку
8. Домашнє завдання

                                      Хід уроку

І Організаційний момент

ІІ Повідомлення теми та мети уроку

На попередніх уроках ми з вами розглянули теореми косинусів, синусів, наслідки з них, ввівши поняття розв’язування трикутників, розглянули основні типи таких задач. Мета сьогоднішнього уроку – узагальнити і систематизувати набуті знання з даної теми та показати їх практичне застосування.

ІІІ Мотивація навчальної діяльності учнів

Обговорюємо з учнями, застосувавши метод «Мікрофон»:

• Для чого вивчаємо тему «Розв’язування трикутників»?
• Чи потрібні ці знання в щоденному житті?

ІV Актуалізація опорних знань

За допомогою  технології « Незакінчене речення» повторимо  теорію

• У трикутнику  проти  більшої сторони лежить….
• Проти меншого кута лежить …
• Сторони трикутника пропорційні…
•  Кожне з попередніх відношень дорівнює…
• Квадрат будь- якої сторони трикутника дорівнює сумі квадратів…
• У попередній формулі знак «+» беремо тоді,…
• Які теореми треба знати, щоб розв’язати трикутник?

V Узагальнення та систематизація знань учнів

Заслуховуємо історичну довідку про теореми косинусів та синусів.

Після прослуховування  задаю запитання учням класу:

Коли була доведенна теорема синусів? Яка теорема була доведенна в «Началах» Евкліда? Хто і коли надав їй сучасного вигляду?

Слайд №1

             Основні задачі на обчислення елементів довільних трикутників. Слайд- таблиця виготовлена двома учнями вдома. Після розбору таблиці задаю учням запитання :

1. Що означає розв’язати трикутник?
2. За якими трьома елементами не можна розв’язати трикутник?

      3 При якій умова можна отримати два розв’язки

 Слайд №2

Метод «Спіймай помилку»

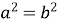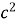• +-2bc cosB

• cos α =

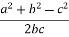
• якщо  sin α = 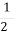то  α =60̊
• α=90̊- (β+γ)

• =  

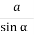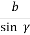
   VI   Закріплення вмінь і навичок

Ми сьогодні здійснимо подорож у світ професій які тісно пов’язані з практичним застосуванням умінь розв’язувати трикутники

Застосування в геодезії

Повідомлення учня про професію геодезиста

Задача№1

Необхідно побудувати міст через річку з точки А в точку В. Інженер з’ясував, що відстань від точки А до точки С дорівнює 100м, і в отриманому трикутнику АВС кут А дорівнює 96̊, а кут В дорівнює 47̊. Якої довжини буде міст?

.

Застосування в астрономії

 Повідомлення учня про  науку астрономію

Задача №3

Астроном вибрав час, коли Планета перебувала на максимальній відстані від Сонця ). Кут між Сонцем і Планетою дорівнює 38̊. Відомо, що Сонце знаходиться на відстані 148800000 км від Землі. Яка відстань від Сонця до Землі?

Задача №4

Застосування в навігації  

Повідомлення учня про  навігацію, картографію

Задача №2

• Знайти відстань від точки А, в якій знаходиться корабель в  даний момент часу до маяка на березі, якщо з цієї точки видно   маяк під кутом 60° до курсу , а через деякий час корабель буде знаходитись в точці В –  на відстані 50 км від точки А, і з точки В даний маяк видно під кутом 110° до курсу корабля

• Доглядач маяка на верхньому поверсі бачить човен, що терпить лихо, під кутом 37̊. Висота маяка дорівнює 100,5км. Яка відстань від маяка до човна?
• Берегові радіомаяки розташовані на відстані 10км. Із судна за допомогою радіолокаційної станції, що знаходиться на судні, визначено відстані до маяків - 2км і 11км відповідно. Знайти кути пеленгів радіомаяків.

Кожна задача- новий слайд

Під час розв’язування задач учні виконують схематичні  малюнки

VII Підсумок уроку та оцінювання учнями уроку

• Урок був цікавим тому,що…
• Я переконаний,що….
• Я думаю, що….

Виконайте схематичний рисунок трикутника, домалюйте обличчя, що передає ваш настрій. Це і буде оцінка уроку

VIIІ Завдання додому

1.Скласти задачу на використання умінь розв’язувати трикутники іншими професіями

2.Підгутувати повідомлення  про такі професії