Урок геометрії "Площі фігур"
ТЕМА: Площі фігур.
НАВЧАЛЬНА МЕТА: Перевірити знання формул для обчислення площ
найпростіших плоских фігур ; формувати уміння
і навички застосовування їх до розв’язання задач.
РОЗВИВАЮЧА МЕТА: Розвивати логічне мислення та пізнавальний
інтерес, формувати загальну культуру мислення,
вчити послідовно та чітко висловлювати свої
думки і впевнено їх захищати.
ВИХОВНА МЕТА: Створювати умови для розвитку творчої
особистості, відповідальності, колективізму, повагу
до товаришів та їхньої думки.
ОБЛАДНАННЯ: завдання на картках, математичне лото, відривний
календар з формулами, малюнки.
ХІД УРОКУ:
І. Організаційний момент.
Клас об’єднується в п’ять груп, вибираються керівники груп. Мета кожної групи якомога швидше і правильно розв’язати завдання запропоновані вчителем.
І І. Підготовчий етап.
Питання до груп.
- Сформулюйте властивості площі для простих фігур.
- Що таке прямокутник?
- Як знайти площу прямокутника?
- Назвіть властивості прямокутника.
- Що таке квадрат?
- Чому дорівнює площа квадрата?
- Що таке паралелограм?
- Як знайти площу паралелограма?
- Що таке трикутник?
- Як знайти площу трикутника?
- Що таке ромб?
- Чому дорівнює площа ромба?
- Що таке трапеція?
- Як знайти площу трапеції?
І І І . Розшифрувати вислів.
На дошці відривний календар з написами з двох сторін. На одній стороні формула, на іншій слово. Учитель звертається до учнів: “Діти , знайдено аркуші паперу із розмитими цифрами, знаками, буквами( їх позначено зірочками). Відновивши формулу з оберненої сторони відкриваєте вислів відомого угорського математика .”
Розмиті формули:
-
S =
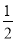 * b ;
* b ;
- S = * b;
-
S =
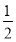 a * ;
a * ;
- S = *2;
-
S =
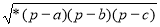 ;
;
-
S =
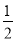 d1*;
d1*;
-
S =
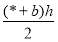 ;
;
-
S =
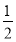 *bsin λ;
*bsin λ;
- S = * h;
- S = a b *;
-
S =
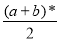 ;
;
-
S =
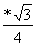 .
.
Учні пояснюють , що стоїть замість зірочки і відкривають вислів.
“ Математика цікава тоді, коли дає поживу нашій винахідливості і здатності до міркувань.” Д’йорд Пойа. Цей вислів буде епіграфом нашого уроку.
IV. Математичне лото.
Кожна група вибирає велику картку із завданнями і на протязі 7хв розв’язує завдання на картці та записують розв’язки в зошит. Учитель називає відповіді, група вибирає картку із своєю відповіддю і накриває відповідне завдання. Якщо відповіді вибрані вірно велика картка закрита певним малюнком.
КАРТКА 1.
|
Знайти площу трапеції, якщо її основи дорівнюють 7,5см і 10,5, а висота 11см.
|
|
Знайти площу квадрата, якщо його периметр дорівнює 20 см.
|
|
Знайти площу ромба, сторона якого 21 см, а висота 10,5 см.
|
Відповідь: 1) 99см2, 2) 25см2, 3)220,5см2.
КАРТКА 2.
|
Знайти площу ромба, діагоналі якого дорівнюють 15 см та 20 см.
|
|
Знайти площу паралелограма, основа якого дорівнює 25 см, а висота 10 см.
|
|
Знайти площу прямокутного трикутника, катети якого дорівнюють 11 см та 20 см.
|
Відповідь: 1) 150см2; 2) 250см2; 3)110см2.
КАРТКА 3.
Знайти площу паралелограма, сторони якогодорівнюють 10 см і 15 см, а кут між ними 30°.
|
|
Знайти площу трикутника, основа якого 10 см, а висота 7 см.
|
|
Знайти площу ромба, діагоналі якого 25 см і 16 см.
|
Відповідь: 1) 75см2; 2) 35см2; 3) 200см2.
КАРТКА 4.
|
Обчислити площу трапеції з основами 9 см і 11 см та висотою 8 см.
|
|
Знайти площу прямокутного трикутника, катети якого дорівнюють 35 см і 20 см.
|
|
Знайти площу ромба, сторона якого дорівнює 11см, а висота 7 см.
|
Відповідь: 1) 80см2; 2) 350см2; 3)77см2.
КАРТКА №5.
|
Знайти площу трикутника зі сторонами 12 см і 10 см та кутом між ними 30° |
|
Знайти площу трапеції з основами 15 см та 20 см і висотою 8 см. |
|
Знайти площу ромба з діагоналями 12 см та 8 см. |
Відповідь: 1) 30 см2; 2)140 см2; 3) 48 см2.
V. Розв’язання задачі.
Кожна група отримує окреме завдання.
Задача №1.
В рівнобічній трапеції АВСД з тупим кутом В рівним 120° та бічною стороною АВ, що дорівнює 8см, знайдіть висоту. (![]() )
)
Задача №2
В рівнобічній трапеції АВСД з бічною стороною АВ=8см , діагональ є бісектрисою гострого кута. Знайдіть меншу основу трапеції. ( 8 см. )
Задача №3.
В рівнобічній трапеції АВСД з бічною стороною АВ=8см, висота рівна ![]() см. Знайдіть більшу основу трапеції, якщо її менша основа дорівнює бічній стороні. ( 16см )
см. Знайдіть більшу основу трапеції, якщо її менша основа дорівнює бічній стороні. ( 16см )
Задача №4.
Знайдіть площу рівнобічної трапеції з основами 8см та 16см і висотою ![]() см. (48
см. (48![]() см2)
см2)
До дошки виходить представник групи із задачею №1, будує малюнок, усно повідомляє умову, записує розв’язок. Потім виходить представник групи із задачею №2 і з тим же малюнком продовжує розв’язання ...
Коли всі 4 задачі розв’язані учні роблять висновок, що розв’язали одну задачу з умовою
“ В рівнобічній трапеції АВСД з тупим кутом В=120° і бічною стороною АВ=8 см, діагональ є бісектрисою гострого кута. Знайдіть площу трапеції.”
VI. Логічне завдання.
Кожній групі необхідно розв’язати задачу на “розрізання фігур”
Розрізати дану фігуру на 4 рівні за площею і формою фігури.
VII. Домашнє завдання.
- Діагоналі ромба відносяться як 12:5, а сторона ромба дорівнює 26 см. Знайдіть площу ромба.
- Діагональ рівнобічної трапеції є бісектрисою гострого кута, а її основи відповідно дорівнюють 7см і 15см. Знайдіть площу трапеції.
VIII. Підведення підсумків уроку .


про публікацію авторської розробки
Додати розробку
