Урок геометрії "Розв'язування трикутників"

Клас: 9Б

Тема уроку. Розв’язування трикутників

Очікуванні результати:

                      формування  предметних  компетентностей:

• домогтися  розуміння , що означає «розв’язати трикутник»;
• вміння  розв’язувати трикутники за відомими елементами

                       формування ключових компетентностей:

• формувати вміння вибирати і використовувати                   

                          необхідну інформацію для розв’язування задачі;

• формувати здатність висловлювати власну думку,

                        слухати і чути інших, ефективно співпрацювати в парі;

• сприяти самовихованню чесності, активності.

Тип уроку: комбінований

Обладнання та наочність: інструктивна картка для учнів,  таблиця 2, пам’ятка   для учнів,  умови задач, дошка, проектор, ноутбук.

 

                                       Математика  цікава тоді, коли живить

                                      нашу  винахідливість  і  здатність  міркувати.

                                                                                                                  Д. Пойа

                                                              Хід уроку

І. Організаційний етап

ІІ. Повідомлення теми і мети уроку

     Мотивація навчальної діяльності

На попередніх уроках ви розглянули теореми синусів, косинусів та наслідки з них, знаємо теорему про суму кутів трикутника.

 Сьогодні перед нами стоїть завдання:

                -повторити все, що вивчили;

                -пригадати те, що забули;

                -вміло застосовувати отримані знання до розв’язування геометричних  задач.

Зверніть увагу на «Пам’ятку для учнів».

Ознайомтесь, будь-ласка, із запропонованими вам рекомендаціями.

 

                                     Справжній скарб для людини -  вміння трудитися.

                                                                                                                     Езоп

                                 Пам’ятка для учнів

1.Будь уважним.

2.Міркуй, шукай ,порівнюй, роби висновки, працюй.

3.Шукай нові способи розв’язування проблеми.

4. Самостійно встановлюй зв’язки відомого з невідомим.

5. Будь наполегливим і не бійся помилитися.

6. Експериментуй та виправляй невдалі спроби.

7. Будь упевнений у своїх здібностях.

Історична довідка

Вчені Індії, зводили розв’язування будь-яких трикутників до розв’язування прямокутних і не потребувати теорему синусів і не знали її. Ця теорема була доведена лише в одинадцятому столітті видатним астрологом ал-Беруні. Теоремою синусів користувалися, починаючи з XVІ ст. і європейські математики.

Теорема косинусів була доведена, звичайно, геометрично ще в «Началах» Евкліда. Словесно теорема косинусів була вперше сформульована французьким

математиком Француа  Вієтом в XVІ столітті.

Сучасний вид теореми косинусів приймає в 1801 році французького математика Лазара Карно.

 

ІІ. Актуалізація опорних знань

Вказати назви сформульованих теорем.

Теорема 1.

Сторони трикутника пропорційні до синусів протилежних кутів.

                                                                                   (теорема синусів)

 

Теорема 2.

Квадрат сторони трикутника дорівнює сумі квадратів двох інших його

сторін без подвоєного добутку цих сторін на косинус кута між ними.

                                                                                  (теорема косинусів)

Запишіть їх за допомогою формул.

  1)  = 2R

  2)

2. Замість … вставити пропущені слова:

    1. У будь-якому трикутнику відношення сторони до … дорівнює діаметру кола, описаного навколо цього трикутника (синуса протилежного кута)

    2.  У трикутнику проти … лежить більший кут, проти більшого кута лежить … (більшої сторони, більша сторона)

    3. Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін «±» подвоєний добуток однієї з них на проекцію другої знак «+» беремо тоді, коли протилежний кут …, а знак «-» коли …

    4.   Теорему косинусів називають іноді узагальненою теоремою (Піфагора)

    5.   … і … трикутника  називаються основними його елементами

                                                                                             (сторони    кути)

    6. Розв’язати трикутник означає: за даними … основними елементами трикутника … При цьому серед заданих основних елементів хоча б один повинен бути … (трьома; знайти три інші його основні елементи;стороною трикутника).

     3.Використовуючи малюнок,  заповни пропуски у таблиці:

 

 

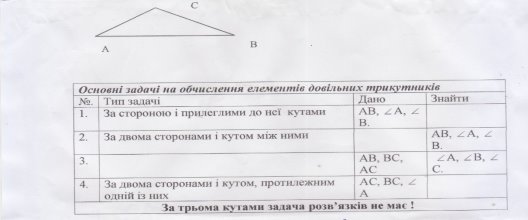
 ІІІ. Застосування знань і вмінь

Задача 1

                                                                                                    Дві сторони трикутника дорівнюють 5см                                       і 7см, а кут між ними 60.Знайдіть                                           третю сторону трикутника.

 

                            Розв’язання

    Нехай АС=5см, АВ=7см, а кут між ними 60 (А=60). Використовуючи теорему косинусів маємо:

    =+-2АВ*АС*

    =25+49 -2*5*7*=39

    ВС=

    Відповідь: .

 

 

Задача 2

Сторона трикутника дорівнює 10см, а прилеглі кути 45 і  75. Знайти сторону протилежну до кута 45.

 

                             Розв’язання

          Нехай АС=10 см,    ∠А=45, і ∠С=75, ВС-сторона, яка лежить проти кута 45.   

           Використовуючи теорему синусів маємо:

                ;   ∠В= 180-(45+75)=60

     Відповідь:                                                                           

 

Задача 3

Футбольний м’яч лежить у точці футбольного поля на відстані 23м і 24м від основ В і С стійок воріт. Футболіст спрямовує м’яч у ворота. Знайти кут попадання м’яча у ворота, якщо ширина воріт 7м.  (колективно)

 

 

 

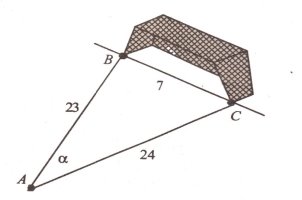
Задача 4

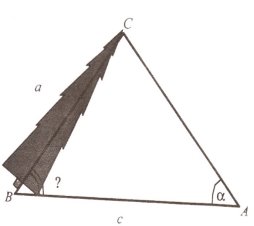Знайти кут нахилу ялинки після бурелому, якщо її висота дорівнює α, і вершину ялинки спостерігач бачить під кутом α   з точки А, яка знаходиться на відстані с від основи ялинки.

 

Задача 5. Робота в парах

 Обговоріть план виконаних завдань, розподіліть завдання варіанта 1, а хто

 варіанта 2. Виконайте завдання і здійсніть взаємоперевірку.

 Варіант 1

У трикутнику АВС сторона АВ дорівнює 7, а ∠В-60, ∠ С-45. Розв’яжіть

 трикутник АВС.

  Варіант2

У трикутнику АВС сторона ВС дорівнює 7, ∠ В-45, ∠ С-30. Розв’яжіть трикутник АВС.

 

 

 

 

 

Робота біля дошки

Задача. На будівництві залізниці потрібно на ділянці АВ прокласти тунель. За даними на малюнку визначте довжину тунелю.

Розв’язання.

З трикутника АВС за теоремою косинусів:

;

 

  (м).

MN=AB-AM-NB=775-93-146=536 (м).

 

ІV. Підсумок уроку

    Перегляд  відеофільму «Пізанська вежа».

    Нині  вежа має нахил 4 градуси від вертикальної  осі.

 

 

V. Домашнє завдання:

Опрацювати   §15.  Розв’язати №501 (а), №503 (а).