Урок геометрії у 8 класі Тема: "Середня лінія трапеції та її властивості"

Середня лінія трапеції

та її властивості

Урок провела

 у 8 - А класі

НВК «Ерудит» м. Києва

Ікол Наталя Василівна

Тема: Середня лінія трапеції та її властивості

Цілі: формування компетентностей:

• предметна компетентність: сформувати поняття середньої лінії трапеції; розвивати вміння розв’язувати задачі, застосовуючи властивості середньої лінії трапеції; показати практичне застосування геометрії в повсякденному житті;
• ключові компетентності:

• формувати вміння чітко, лаконічно та зрозуміло формулювати власну думку;
• сприяти самовихованню свідомого ставлення до навчання.

Тип уроку: урок вивчення й первинного закріплення нових знань.

Обладнання: комп’ютер, проектор, екран, е-підручники.

Хронометраж уроку:

1. Організаційний момент – 1 хв.
2. Актуалізація опорних знань – 4 хв.
3. Мотивація навчальної діяльності – 2 хв.
4. Вивчення нового матеріалу – 22 хв.
5. Засвоєння нових знань та вмінь – 10 хв.
6. Підсумок уроку – 5 хв.
7. Домашнє завдання – 1 хв.

ХІД УРОКУ

1. Організаційний момент

Перевірка готовності класу до уроку. Побажання гарного настрою, позитивного спілкування, активної роботи. 

Пропоную розпочати урок з висловлювання: Слайд № 1.

«Математику не можна вивчати, спостерігаючи, як це робить сусід».

Нелін

2. Актуалізація опорних знань.

Фронтальне опитування означень і теорем за допомогою «Хмар тегів». Слайд № 3-5

Паралельні прямі, які перетинають сторони кута і відтинають на одній із них рівні відрізки, відтинають рівні відрізки і на іншій стороні

Середня лінія трикутника сполучає середини двох його сторін, паралельна третій і дорівнює її половині

Трапеція – це чотирикутник, у якого дві сторони паралельні, а інші дві ні

Сьогодні наш урок присвячено трапеції. Дайте, будь ласка, означення трапеції англійською, німецькою та французькою мовами.

Існує особлива мова, що зрозуміла кожній людині, якою б мовою вона не володіла. Це – рисунок. Сьогодні на уроці ми будемо постійно звертатися до рисунків, розв’язувати задачі за готовими рисунками. Ви продемонструєте вміння застосовувати знання під час розв’язування задач на трапеції.

Виконання завдань за готовими рисунками Слайд № 6

3. Мотивація навчальної діяльності

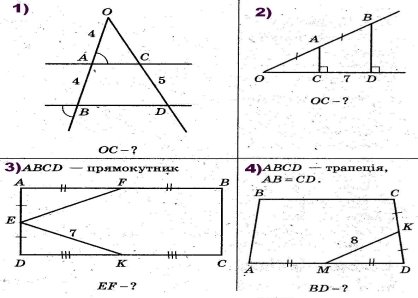
Проблемне питання Слайд № 7

Над входом у дачний будинок є навіс. Згодом виникла потреба поставити підпори до середини навісу. Як, не вимірюючи, можна знайти довжину підпори, якщо відповідні краї навісу віддалені від поверхні землі на 2,5 м і 3,5 м?

Поміркуємо над геометричним рисунком цієї задачі. Слайд № 8

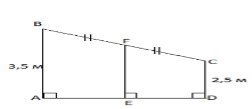
Як ви вважаєте, чи можна на практиці, не застосовуючи безпосередньо вимірювання, а використовуючи тільки знання з геометрії, визначити довжину підпори?

 На це питання ми зможемо дати відповідь після того, як розглянемо тему «Середня лінія трапеції та її властивості».

4. Вивчення нового матеріалу. Слайд № 9-10

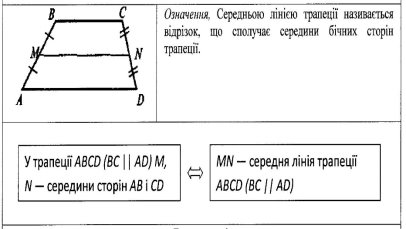
Усні вправи за означенням Слайд № 11-12

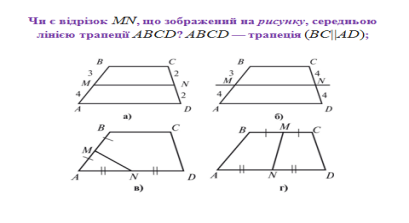
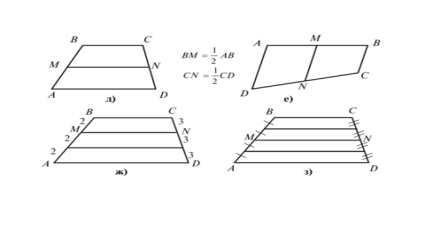
ПОВІДОМЛЕННЯ ДОСЛІДНИКІВ

Трапеція, з давньогрецької, означає «столик». Уперше зустрічається в давньогрецького математика Посідонія. Припущення про те, що середня лінія трапеції дорівнює півсумі її основ, було відоме давнім єгиптянам. Його зміст записаний у папірусі Ахмеса та стінах храму Едфу у Верхнім Єгипті.

Новинки в архітектурі із застосуванням трапецій.

Французький архітектор Леопольд Віторг створив проект і побудував приміщення школи, у якій підлога має форму трапеції. Стіл учителя стоїть у більшій основі трапеції. Зменшується кількість учнів, які сидять за партами. Учні, які сидять за партами, поставленими вздовж стін, краще бачать записи на дошці, вони не закривають один одного спинами. А це краще для здоров’я – зберігається зір, не порушується постава. Адже школярам не доводиться нахилятися вбік.

У повітряних лініях силових електропередач використовують багатожильний дріт круглого перерізу. У круглому дроті проміжки між жилами займають чверть об’єму. Дослідники з канадської фірми «Октарі-гідро» розробили дріт із жилами, переріз яких є трапецією. У цьому перерізі об’єм проміжків між жилами знизився на 50%, а це призвело до значного підвищення електропровідності.

Властивості середньої лінії трапеції

Сформулювати та довести властивість середньої лінії трапеції (використання програмного забезпечення GeoGebra). Слайд №13-15

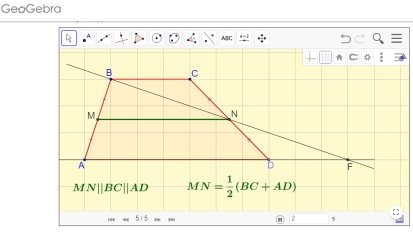
Розглянемо інші властивості трапеції. Слайд № 16

Учні малюють різні трапеції: 1 варіант – рівнобічну, 2 варіант – прямокутну.

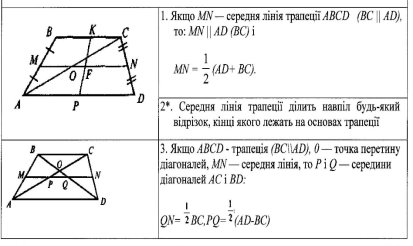
Усні вправи за властивостями середньої лінії. Слайд №17-18

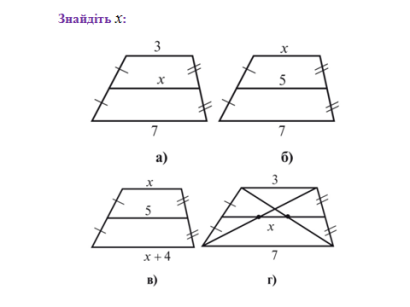
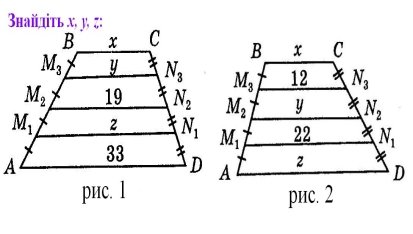
Розв’язування «проблемної задачі» Слайд № 19

Учні обчислюють довжину підпори  FE як довжину середньої лінії трапеції.

FE = (2,5+3,5)/2 = 3(м)

Відповідь: довжина підпори 3 метри.

5. Засвоєння нових знань та вмінь

Розв'язування задач за допомогою програми LearningApps . Слайд № 20-21

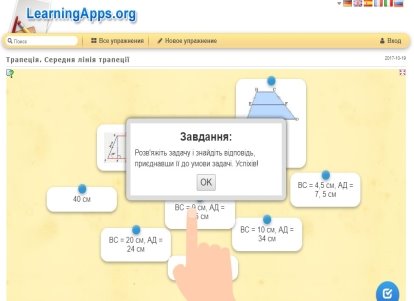
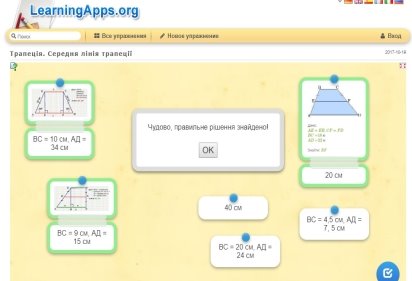
6. Підсумок уроку

Графічний диктант

1. Середньою лінією трапеції називають відрізок, що сполучає середини будь-яких її сторін.
2. Середня лінія трапеції дорівнює сумі основ.
3. Середньою лінією трапеції називають відрізок, що сполучає середини її бічних сторін.
4. Середня лінія трапеції паралельна основам трапеції.
5. Середня лінія трапеції проходить через точку перетину діагоналей трапеції.
6. Середня лінія трапеції дорівнює півсумі бічних сторін.
7. Середня лінія трапеції ділить навпіл будь-який відрізок, кінці якого лежать на основах трапеції.

Ключ до диктанту: - - ^^- - ^

Розв'язування вправи «Знайди ключове слово» за допомогою програми LearningApps. Слайд № 22-23

Ключове слово: СЕРЕДНЯ ЛІНІЯ

7. Домашнє завдання Слайд № 24

Вивчити основні властивості середньої лінії трапеції;

п. 8, №244, 261, 259/263;

Створити хмари тегів на тему: «Чотирикутники та їхні властивості».