Урок геометрії у 9 класі "Підсумковий урок з теми:"Розв'язування трикутників""

Підсумковий урок з теми: «Розв’язування трикутників»

Мета уроку.

Навчальна. Узагальнити та систематизувати знання за темою: «Розв’язування трикутників», зокрема повторити формули для знаходження площі трикутника; теорему синусів і косинусів та наслідки з них; навчити учнів розв’язувати трикутники для розв’язування прикладних задач;  

Розвиваюча. Формувати вміння розпізнавати проблему, стисло та зрозуміло формулювати власну думку, розвивати інтерес до вивчення математики.

 Виховна. Виховувати відповідальність, уважність, працьовитість.

 

Обладнання. Комп’ютер, презентація, роздатковий матеріал.

Очікувані результати:

Після уроку учні зможуть:

повторити основний теоретичний матеріал про трикутник;

удосконалити свої вміння й навички розв'язування задач з теми «Трикутники»;

робити логічні висновки, аналізувати вивчений матеріал;

поглибити вміння оцінювати свої знання.

Учні повинні знати:

теореми косинусів і синусів та наслідки з них,

співвідношення між кутами трикутника і протилежними сторонами;

формули для знаходження площі трикутника.

Учні повинні вміти:

застосовувати теореми синусів і косинусів та наслідки з них до розв’язування трикутників,

знаходити невідомі елементи трикутника за трьома відомими,

застосовувати набуті знання при розв’язуванні прикладних задач

 

Тип уроку:  узагальнення та систематизація знань.

Розум - це не тільки знання,  

а й уміння застосовувати знання на ділі.

Арістотель

Хід уроку.

 

І. Організаційний момент. Повідомлення теми і мети уроку

Трикутник… знайомий вам з дитинства, і починаючи з 7 класу, з уроків геометрії, геометрична фігура, містить в собі чимало цікавого та загадкового.

На попередніх уроках ви розглянули  теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників, розглянули основні типи задач на обчислення елементів довільних трикутників, вивчили формули для знаходження площі трикутників.

Сьогодні  перед нами стоять такі завдання:

•     повторити все, що вивчили;
•     пригадати те, що забули;
•     вміло застосовувати отримані знання до розв’язування геометричних та прикладних задач.

Незважаючи на те, що попереду у нас велика пізнавальна робота, я сподіваюсь, що ми зможемо зберегти гарний настрій до кінця уроку.

Трикутник є однією з найпростіших і найважливіших фігур на площині Завдяки жорсткості форми, трикутник є обов'язковим «будівельним» елементом майже всіх складних геометричних конструкцій. Довкола трикутника формується курс елементарної геометрії.

Уміння знаходити площу трикутника та елементи трикутника – одна з найактуальніших задач геометрії. Її розв’язання залежить від глибини  наших знань. .ІІ. Перевірка домашнього завдання.

1. Відповіді до завдань на екрані

 2.  ДПА-2019

1) 1 учень Варіант 40 (№1.11)

2) 2 учень Варіант 30 (№1.11)

3) 3 учень Варіант 31(№1.11)

4) 4 учень Варіант 42(№1.11)

 

ІІІ. Актуалізація опорних знань.

1. Відповідаючи на запитання, ми повторимо теоретичний матеріал з розділу «Розв’язування трикутників»

1)Що означає розв’язати трикутник?

2) Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?

3) Які теореми потрібно знати, щоб розв’язати трикутник?

4) Сформулюйте теорему косинусів.

5) Яку властивість для діагоналей паралелограма можна довести за допомогою теореми косинусів?

6) Сформулювати теорему синусів.

7) Сформулюйте наслідок із теореми косинусів про співвідношення сторін трикутника.

8) Сформулювати наслідок з теореми синусів про діаметр кола, описаного навколо трикутника.

 

2. Оскільки сьогодні на уроці ми будемо розв'язувати задачі на знаходження площі трикутника за допомогою формул, пропоную зробити шпаргалку. У кожного з вас на парті є таблиця. Ви повинні її заповнити.

3.Виконання інтерактивних вправ на повторення формул площі трикутника.

 

IV. Узагальнення вмінь та навичок учнів з теми через розв'язування задач.

Задача 1.

Укажіть вид трикутника, довжини сторін якого дорівнюють 2 см, 4 см і 5 см.

А) тупокутний;

Б) Гострокутний;

В) Прямокутний;

Г) Визначити неможливо.

Задача 2.

Сторони трикутника дорівнюють: 1, 4 і . Знайдіть градусну міру найбільшого кута цього трикутника.

А) 75°;

Б) 60°;

В) 120°;

Г) 90°.

Задача 3.

У трикутнику АВС В = 105°, А =30°. Знайдіть відношення

А) ;

Б) ;

В) ;

Г) .

Задача 4.

Площа трикутника АВС дорівнює 16 см кв. Знайдіть sinВ, якщо ВС=8 см, АВ=10 см.

А) ;

Б) ;

В) ;

Г) .

Задача 5.

Сторони паралелограма дорівнюють 2 см і см, а гострий кут становить 60°. Знайдіть висоту паралелограма, проведену до меншої сторони.

А) 3 см;

Б) 12 см;

В) 6 см;

Г) см.

Задача 6.

Дві сторони трикутника дорівнюють 4 см і 8 см, а кут між ними -60°. Знайдіть третю сторону трикутника та його площу.

Учитель .

В сучасному житті потрібно бути компетентними у різних сферах: наприклад, порахувати кошторис для проведення ремонтних робіт в квартирі, розбити клумбу біля свого будинку тощо. Тому сьогодні ми розв’яжемо прикладні задачі з реального життя.

Прикладна задача – це задача, що виникла зовні математики, але для її розв’язування потрібно використати математичні моделі. Такі задачі розкривають багатогранність застосування математики в житті. Предмети, які нас оточують мають форму геометричних фігур. Вікна, двері наших будинків мають форму прямокутників і трикутників. Щоб споруди були стійкими і міцними, окремим їх деталям надають форму трикутника. Елементи, майже кожної будівельної конструкції виготовляють так, щоб вони мали якомога більше трикутників. Їх можна побачити у мостових формах, телевежах, кронштейнах.

 

V. Робота в групах.

 Розв’язання.

АВС=180° - (80° +72° )= 28°. За теоремою синусів:

   ,      ;           ,  

Відповідь: 101,29 м.

 

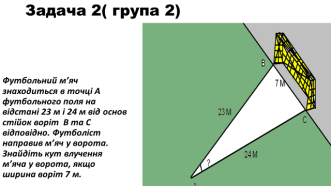
Розв’язання.

Розглянемо трикутник АВС, вершинами якого є точки А, В, С. За теоремою косинусів 

ВС² = АС² + АВ² – 2 ∙ АС ∙ АВ ∙ cos ВАС. ВАС – шуканий кут.

За наслідком із теореми косинусів cos ВАС = ,

cos ВАС = = 0,9565; ВАС=17°.

Відповідь: ВАС=17°.

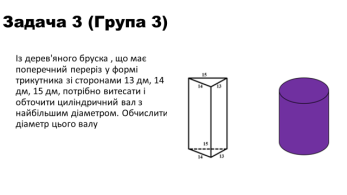
Розв’язання.

Діаметр валу – це діаметр круга, який вписано у трикутник зі сторонами 13 дм, 14 дм і 15 дм.

За формулою  Герона знайдемо площу трикутника зі сторонами 13 дм, 14 дм і 15 дм.

S = , де а, b, с – сторони трикутника, р =   – півпериметр.

р =   S = ;  S =84 см²

=;     =;     R=8, 125 дм; D=8,1252=16,25 дм.

Відповідь: 16,25 дм.

VI. Підбиття підсумків

Метод «Чотири ЩО?»

1. Що ви дізналися, навчилися на уроці?
2. Що сподобалося найбільше?
3. Що було найскладнішим?
4. Що треба ще вивчити?

VII.Домашнє завдання

1. Відстань між трьома селами 4 км, 13 км, 15 км. На якій відстані від кожного села треба поставити вишку мобільного зв'язку, щоб прийом сигналу був однаковий у всіх трьох селах.

2. Комунальним працівникам на алеї необхідно розбити три однакових клумби, кожна з яких має форму рівностороннього трикутника. Висота кожного трикутника дорівнює 2 метри. Яку площу займатимуть клумби?

3. Щоб дістатися поглядом верхівки дерева від підніжжя будинку, потрібно

дивитися вгору під кутом 22°, а щоб  побачити верхівку дерева з балкона , що розташований на відстані 50 метрів над поверхнею землі, слід дивитися вниз під кутом 50° . Знайдіть:

а) висоту дерева;

  б) відстань від дерева до будинку.

VIII.  Рефлексія

Метод  «Похвали себе».

Учні вказують на позитивні сторони своєї роботи на уроці.