Тема уроку. Побудова перерізів многогранників.

Мета уроку: формування вмінь учнів застосовувати властивості паралельних площин до розв'язування вправ, побудови перерізів.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання.

1. Три учні відтворюють розв'язування задач № 28, 30, 31 на дошці, в цей час клас пише математичний диктант.
2. Математичний диктант.

Через вершини А, В, С, D: варіант 1 — паралелограма АВСD (рис. 76). Варіант 2 — трапеції АВСD (рис. 77), які лежать в одній із паралельних площин α, проведено паралельні прямі, що перетинають другу площи­ну β в точках А₁, В₁, С₁, D₁.

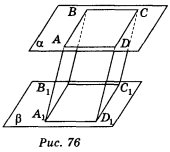
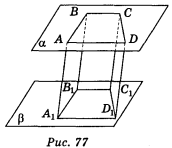
Користуючись зображенням, запишіть:

1) пряму, яка лежить у площині β і паралельна прямій АС; (2 бали)

2) відрізки, довжини яких дорівнюють АА₁; (2 бали)

3) чому дорівнює кут А₁АD₁, якщо АА₁D₁ = 120°; (2 бали)

4) чому дорівнює довжина діагоналі ВD, якщо В₁D₁ = 3 см; (2 бали)

5) вид чотирикутника А₁B₁С₁D₁; (2 бали)

6) чому дорівнює площа чотирикутника А₁В₁С₁D₁, якщо площа чо­тирикутника АВСВ дорівнює 30 см². (2 бали)

Відповідь. Варіант 1. 1) А₁C₁; 2) ВВ₁, СС₁, DD₁; 3) 60°; 4) 3см;                           5) паралелограм; 6) 30 см².

Варіант 2. 1) А₁C₁; 2) ВВ₁, СС₁, DD₁; 3) 60° ; 4) 3см;

5) трапеція; 6) 30 см².

3. Перевірка виконання математичного диктанту, заслуховування розв'язування задач № 28, 30, 31 та відповіді на запитання учнів, що виникли в процесі розв'язування цих задач.

II. Закріплення та осмислення знань учнів

Формування вмінь учнів будувати перерізи многогранників, використовуючи властивості паралельних площин

Властивість паралельних площин широко застосовується при розв'я­зуванні задач, зокрема задач на побудову перерізів.

Задача.

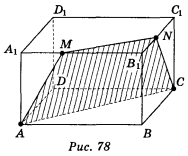
Побудувати переріз прямокутного па­ралелепіпеда АВСDА₁B₁С₁D₁ площи­ною α, яка проходить через вершини А, С і внутрішню точку М ребра А₁В₁ (рис. 78).

Розв'язання

Переріз площини α з двома гранями одержимо, побудувавши відрізки АС ТАМ. Оскільки площини граней АВСD і А₁В₁С₁D₁ паралельні, то паралельні і їх лінії перетину з площиною α, тому, по­будувавши МN || АС і відрізок МС, оде­ржимо переріз — трапецію АМКС.

Розв'язування задач

1. У трикутній піраміді SАВС провести переріз:

а) через середину ребра АС паралельно грані SСВ;

б) через середину ребра SС паралельно грані SАВ.

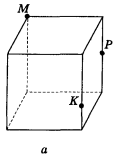
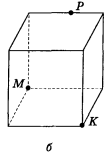
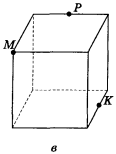
Рис. 79

2. Побудуйте перерізи куба площиною, яка проходить через точки М, К, Р (рис. 79).
3. Дано куб ABCDA₁B₁C₁D₁. Побудуйте переріз куба площиною, яка проходить через дані точки: а) С₁, К, D; б) С₁, К, С, де точка К — середина А₁В₁. З'ясуйте, яка фігура утвориться в перерізі. (Відповідь, а) рівнобічна трапеція; б) прямокутник.)
4. Точка Х ділить ребро АВ куба ABCDA₁B₁С₁D₁ у відношенні АХ : ХВ = 2 : 3. Побудуйте переріз цього куба площиною, яка па­ралельна площині АА₁С₁ і проходить через точку X. Знайдіть пери­метр перерізу, якщо АВ = а.  (Відповідь. .)
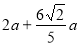5. Доведіть, що коли перерізом паралелепіпеда е шестикутник, то його протилежні сторони паралельні.
6. Чи може перерізом куба бути правильний п'ятикутник?
7. Побудуйте переріз куба площиною, яка проходить через точку Е і паралельна площині MNP (рис. 80).

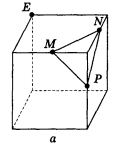
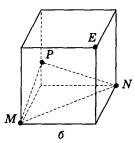
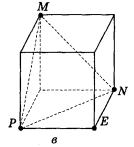
Рис. 80

8. Побудуйте прямокутний паралелепіпед ABCDA₁B₁C₁D₁ і його пере­різ площиною, яка проходить через: а) ребро СС₁ і точку перетину діагоналей грані AA₁D₁D; б) точку перетину діагоналей грані ABCD і паралельно площині АВ₁С₁.
9. Точка А₁ ділить ребро SA тетраедра SABC у відношенні SA₁ : A₁A = 2 : 3. Побудуйте переріз тетраедра площиною, яка прохо­дить через точку А₁ і паралельна площині АВС. Знайдіть периметр і площу перерізу, якщо АВС — правильний трикутник і АВ = 10 см. (Відповідь. 12 см; 7 см².)

III. Домашнє завдання

Розв'язати наступну задачу.

Дано куб ABCDA₁B₁C₁D₁. Доведіть, що переріз куба площиною А₁С₁К, де К — середина DC, є трапеція, а перерізи куба площинами А₁В₁К і АА₁К є паралелограмами.

IV. Підведення підсумку уроку

Усне розв'язування задач

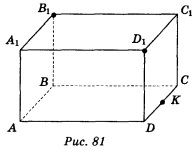
1. ABCDA₁B₁C₁D₁ — прямокутний паралелепіпед. Доведіть, що переріз прямокутного паралелепіпеда площиною, яка проходить через точки В₁, D₁ і К, де точка К — середина ребра CD, є трапеція (рис. 81).
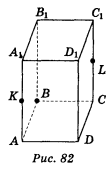
2. ABCDA₁B₁C₁D₁ — прямокутний паралелепіпед (рис. 82). Доведіть, що переріз його площиною, яка проходить через точки В, К, L, де точка К — середина ребра AA₁, а точка L — середина ребра СС₁, є паралелограм.