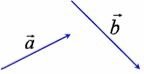
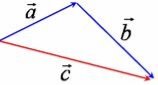
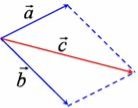
Дії над векторами. Сума і різниця векторів.

 

Тема уроку:    Операції над векторами  

Мета уроку:

• повторити поняття вектора в просторі та пов’язані з ним поняття абсолютної площини, напряму, рівності векторів, види векторів;
• навчити оперувати діями над векторами;
• розвивати просторову уяву, пам'ять, уміння проводити аналогії;
• виховувати наполегливість, працьовитість;
• проявляти ініціативність, відповідальність, упевненість у собі.

Тип уроку. Засвоєння нових знань і вмінь

Наочність та обладнання: презентація «Вектори на площині»; картки-заготовки для с/р, з  формулами та рефлексії.

Очікувані результати.

Учень/учениця: користується аналогією між векторами на площині й у просторі;

Після закінчення уроку учень/учениця:

• знає: що таке добуток та різниця векторів
• вміє: побудувати вектор, суму векторів за правилом трикутника та правилом паралелограма
• може: сформулювати задачу на мові векторів, перетворювати векторні рівності.

 

Хід уроку

 

І. Організаційний момент.

Епіграф нашого уроку:

Ваша сила - віра в себе.

Самостійні думки виникають тільки

із самостійно  отриманих знань.

 К.Ушинський

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 Учні-консультанти доповідають вчителеві про готовність класу до уроку та наявність виконання домашнього завдання учнями. Вчитель відповідає на запитання учнів, які виникли під час виконання домашнього завдання.

ІІІ. ФОРМУЛЮВАННЯ ТЕМИ, МЕТИ І ЗАВДАНЬ УРОКУ

          Поняття вектора є важливим у математиці та фізиці. Існує чимало важливих величин, котрі є векторами. Наприклад, сила, швидкість, прискорення, кутовий момент, напруженість електричного і магнітного полів. Такі величини називають –векторними. Ці величини можна протиставити іншим величинам, таким як маса, об’єм, тиск, температура та густина, які можна описати звичайним числом, їх називають скалярами. Тому знання про вектори є важливими при вивченні природничо-математичних наук.

        Сьогодні на уроці ми повторимо  знання  про вектори в просторі, розглянемо задачі , що передбачають використання  властивостей додавання та віднімання векторів . Оскільки тему «Вектори» ви вже вивчали в курсі геометрії 9-го класу. Спробуємо пригадати відомі нам факти і провести паралель між   векторами на площині і векторами в просторі.

ІV. Актуалізація опорних знань і вмінь учнів

Учні дають відповіді на запитання вчителя

1. Що ми називаємо  вектором  та яке його позначення ?
2. Що ми розуміємо під довжиною вектора, як її позначають?

 

 

 

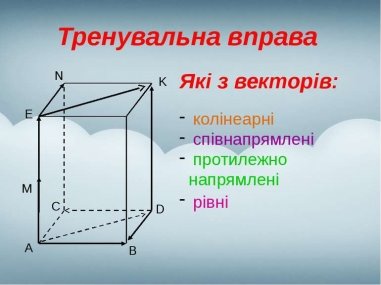
3. Розтлумачити записи:

                  ,   

V. ЗАСВОЄННЯ ЗНАНЬ

СПРИЙМАННЯ І УСВІДОМЛЕННЯ НОВОГО МАТЕРІАЛУ

 

 

 

 

Дії  над векторами

1.  Сума векторів

Правило трикутника	Правило паралелограма
Сумою (+) двох векторів  і  є такий вектор , напрямлений з початку вектора  в кінець вектора  за умови, що початок вектора  збігається з кінцем вектора .	Сумою (+) двох векторів  і  є такий вектор , напрямлений з початку векторів  і  вздовж діагоналі паралелограма, сторони якого утворені з векторів  і  їх паралельним переносом за умови, що початки векторів  та  збігаються.

 

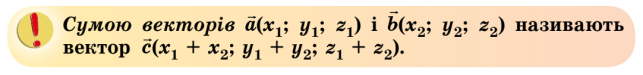
2 Різниця векторів.

Різницею     -        векторів і          називається  вектор     такий, що

Тобто,

 

 

 

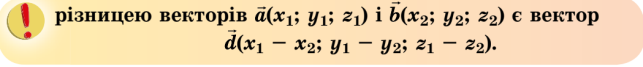
3. Правило многокутника

 

 

Сума декількох векторів знаходиться за допомогою правила многокутника, яке є узагальненням правила трикутника

 

 

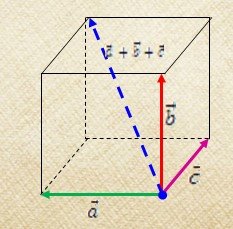
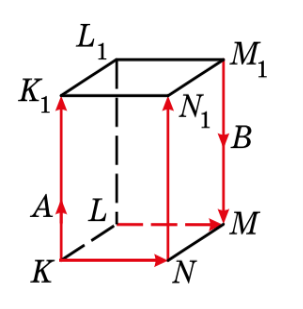
Якщо вектори не лежать на одній площині, та мають початок в одній точці, то використовуємо правило паралелепіпеда, яке є узагальненням правила паралелограма.

 

СПРИЙМАННЯ І УСВІДОМЛЕННЯ НОВОГО МАТЕРІАЛУ

VІ. Осмислення і усвідомлення вивченого матеріалу

1) Усно з коментуванням з місця: № 40.1(При́зма  —фігура, многогранник (призматоїд), у якого дві грані — рівні 3-кутники, розташовані в паралельних площинах, а решта 3 граней — паралелограми.); 40.2

Відпрацювання вмінь та навичок

 Учень працює біля дошки,  клас в цей час самостійно:

№  40.5 та № 40.7, 40.11, 40.13

Побудувати:1)  а-b; b-d; d-b (за правилом трикутника – три учня біля дошки)

                      2) )  а-b; b-d; d-b (за правилом  паралелограма – три учня біля дошки)

VIII. Удосконалення вмінь і навичок

Самостійна робота

Дано вектори а і b (дивись малюнок). Побудувати вектори а + b, a – b,

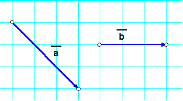Варіант І

 

 

 

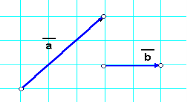Варіант ІІ

 

 

 

 

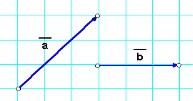Варіант ІІІ

 

 

 

 

 

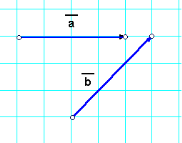Варіант IV

 

 

 

 

 

 

Х. Підсумки уроку за схемою:

Важливо знати:  формулу для обчислення довжини вектора;  що є сумою та різницею   векторів.

Важливо уміти: оперувати векторами, тобто виконувати дії над координатами даних векторів.

XI. Рефлексія (осмислення результатів уроку)

У кожного з вас на парті є по 4 сходинки. Оберіть саме ту на якій ви вважаєте, що знаходитесь після сьогоднішнього уроку.

ІХ. Домашнє завдання:

Опрацювати §40 (ст.. 219-222)

Повторити: дії з векторами  на площині

Виконати:40.8; 40.12; 40.14

 Додаткова задача

ABCD — паралелограм. Які векторні рівності можна записати?