Урок "Геометричні фігури. Точка. Пряма. Промінь."
Тема: Елементарні геометричні фігури та їх властивості
Урок 1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Тема уроку: Геометричні фігури. Точка. Пряма. Промінь.
Тема уроку: Геометричні фігури. Точка. Пряма. Промінь.
Мета: ознайомити учнів із новим для них предметом геометрією, із поняттям найпростіших фігур у геометрії, домагатися свідомого засвоєння термінології, що описує взаємне розташування точок та прямих на площині, формулювання основних властивостей розташування точок та прямих; виробити первинні вміння позначати точки та прямі на рисунку, описувати ситуацію, що зображена на рисунку та, навпаки, за описом ситуації виконувати відповідні рисунки, користуючись найпростішим креслярським приладдям, дати означення променя .
Активізувати пізнавальну діяльність учнів. Виховувати інтерес до вивчення геометрії, до історії розвитку науки.
 “Та не ввійде сюди ніхто з тих, хто не знає геометрії”.
“Та не ввійде сюди ніхто з тих, хто не знає геометрії”.
Платон
Плато́н ( 427 до н. е. — 347 або 348 до н. е.) — давньогрецький мислитель, засновник філософської школи відомої як Академія Платона.
Методичні рекомендації:
Дана тема рекомендована для тих учнів, які мають намір самостійно вивчити і опрацювати тему «Елементарні геометричні фiгури та їх властивості», з подальшим розв’язанням практичних завдань. Надаються історичні відомості про розвиток геометрії. Тема та структура матеріалу повністю відповідають навчальній програмі з математики за курс базової школи.
Матеріали до уроку
З найдавніших часів геометрія вважалася однією з важливих компонент будь-якої освіти взагалі. Насамперед що таке геометрія?
Геометрія була, є і буде постійною супутницею людини на всьому шляху її розвитку, у всій її довгій, складній і цікавій еволюції.
Отже, геометрія – це наука про властивості геометричних фігур.
Пропоную дописати незакінчені речення, використовуючи підручник:
- Геометрія — це наука...
- Планіметрія — це розділ...
- Приклади геометричних фігур.
Основними фігурами на площині є точка й пряма. Як уявляєте собі ці фігури? Точка – це єдина фігура, яку не можна розбити на частини.
При цьому варто зазначити, що пряма нескінченна, а на рисунку завжди зображують частину прямої; щоб розрізняти окремі точки або прямі, їм дають найменування: «точка А», «пряма а». Ознайомтеся із схемою 1:
Основні геометричні фігури та їх комбінації
|
1. Основні геометричні фігури |
|
|
|
|
|
2. Комбінації: основних фігур |
|
|
2) Дві точки і пряма |
|
Промінь |
Відрізок |
|
|
|
|
Два промені |
|
|
а) |
б) |
та із схемою 2:
Розміщення основних геометричних фігур на площині
|
|
Основні фігури: точка А і пряма а |
|
Взаємне розміщення точок і прямих на площині |
|
|
|
Аксіома
Яка б не була пряма, існують точки, що належать цій прямій (А Через будь-які дві точки можна провести пряму і тільки одну
З трьох точок на прямій одна і тільки одна лежить між двома іншими. |
|
Взаємне розміщення прямих на площині |
|
|
|
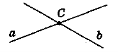
Прямі а і b перетинаються в точці С |
|
|
Прямі а і b паралельні (а || b) |
|
|
|
Поняття «точка належить прямій» має той самий зміст що і слова «точка лежить на прямій», «пряма проходить через точку», використовуємо знаки належності точок фігурі є та заперечення цієї належності ![]() .
.
Запитання:
- Чи можна через одну точку провести пряму і якщо можна, то
скільки? [Можна. Безліч (рис. 1, а).]
- Чи можна через дві дані точки провести пряму? [Можна.]
- Чи можна провести пряму через будь-які дві точки (зазначається інше положення точок)? [Так.] .
- Скільки прямих можна провести? [Тільки одну (рис. 1,6).]
- Чи можна через три точки провести пряму і скільки?
[Можна провести або одну пряму (рис. 1, б), або не можна провести жодної (рис. 1, г).]
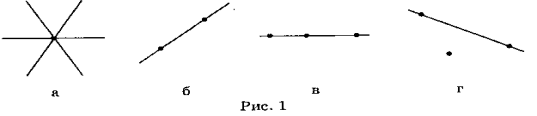
Висновок. Через одну точку можна провести безліч прямих; через дві точки можна провести тільки одну пряму; через три точки можна провести одну пряму, але не через будь-які три точки, а тільки якщо вони розміщені, як показано на рис.1,в.
Запитання:
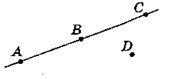
• Використовуючи рис., зробіть висновки щодо точок А, В, С і точок А, С, D. 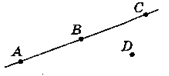
[Якщо точка В лежить між точками А і С, то всі три точки лежать на одній прямій; якщо точки А, С і D не лежать на одній прямій, то жодна з них не лежить між двома іншими.] Основна властивість взаємного розміщення точок на прямій.
Завдання:
• Позначте на прямій три точки так, щоб одна з них лежала між двома іншими. Чи завжди це можливо? [Так.]
• Позначте на прямій три точки так, щоб жодна з них не лежала між двома іншими. [ це неможливо.]
• Який із цього можна зробити висновок? [Із трьох точок на прямій хоча б одна лежить між двома іншими.]
• Чи можна розмістити на прямій три точки А, В і С так, щоб дві з них лежали між двома іншими? [неможливо.]
• Який висновок можна зробити про три точки, що лежать на одній прямій? [Із трьох точок, що лежать на прямій, завжди тільки одна лежить між двома іншими.]
У твердженні аксіоми про розміщення трьох точок на прямій фраза «одна й тільки одна» говорить:
1) про існування на прямій хоча б однієї точки (з трьох), яка має властивість лежати між двома іншими;
2) про єдиність такої точки, їх не може бути дві, три й т. д. Це додатково підтверджується словами «тільки одна».
Оскільки з трьох точок на прямій дві не лежать між двома іншими, то кожна з них розміщена якось інакше відносно інших точок. Якщо, наприклад, точка В лежить між точками А і С, то тоді можна сказати, що точки В і С лежать по один бік від точки А.
ІІІ. Розв’язання задач
Завдання:
-
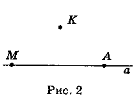
Розгляньте взаємне розміщення точок А, М, К і прямої а (рис. 2). Запишіть висновок, використовуючи знаки
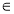 і
і 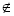 .
.
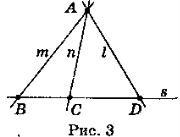
- Використовуючи рис. 3, дайте відповіді:
а) Яким прямим належать точки А, В, С і D?
б) Які прямі проходять через кожну з точок А, В, С, D?
в) Як інакше можна позначити прямі m, п і s?
г) Які точки лежать на прямих АВ і СD?
-
Точки А і B лежать на прямій l. Чи збігаються прямі АВ і 1? Поясніть відповідь. [Точки А і В належать прямій АВ і прямій l, а через дві точки можна провести тільки одну пряму. Отже, прямі АВ і l збігаються.]
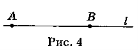
-
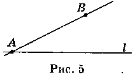 Чи будуть збігатися прямі АВ і l, якщо точка B не лежить на прямій l? Поясніть відповідь. [Не будуть. Якби ці прямі збігалися, то точка B належала б прямій l. А це суперечить умові задачі: точка В
Чи будуть збігатися прямі АВ і l, якщо точка B не лежить на прямій l? Поясніть відповідь. [Не будуть. Якби ці прямі збігалися, то точка B належала б прямій l. А це суперечить умові задачі: точка В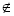 l (рис. 5).] В цьому випадку прямі вважаються різними.
l (рис. 5).] В цьому випадку прямі вважаються різними.
Висновок: прямі будуть різними, якщо хоча б одна точка однієї прямої не належить іншій прямій.
Задача 1 (усно). Відомо, що точка Р лежить між точками М і N. Як розміщені точки: а) М і N; б) М і Р; в) N і Р? [а) По різні боки від точки Р; б) по один бік від точки N; в) по один бік від точки М.]
Задача 2 (усно). Із трьох точок М, N і Р, що лежать на прямій, точки N і Р лежать по один бік від точки М. Яка точка лежить між двома іншими? [Точка М не лежить між точками N і Р. А оскільки кожна з точок МІР може лежати між двома іншими, то дати однозначну відповідь на запитання задачі неможливо.]
Наприклад, із твердження, що точка Р лежить між точками М і N, випливає твердження, що точки М і Р лежать по один бік від точки N (задача 1). Однак із того, що точки М і N лежать по один бік від точки N, ще не можна зробити висновок, що точка Р лежить між точками М і N (задача 2).
Висновок. Якщо з трьох точок одна лежить між двома іншими, то всі три точки лежать на одній прямій, і навпаки, із трьох точок на прямій одна й тільки одна лежить між двома іншими (аксіома).
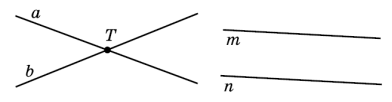
Означення: Якщо дві прямі мають спільну точку, то кажуть, що вони
перетинаються в цій точці. Прямі a і b перетинаються в точці T, а прямі m і n не перетинаються.
Проведемо пряму та позначимо на ній точку A. Ця точка ділить пряму на дві частини, кожну з яких разом з точкою A називають променем, що виходить з точки A. Точка A називається початком кожного з променів. Промені
позначають двома великими латинськими буквами, перша з яких означає початок променя, а друга — деяку точку на промені. Наприклад, промінь OK.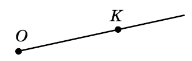
Два промені, що мають спільний початок і доповнюють один одного до прямої, називають доповняльними.
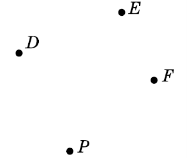 Завдання:
Завдання:
Позначте в зошиті чотири точки D, E, F, P.
1) Через кожні дві точки проведіть пряму. Запишіть назви всіх цих прямих.
2) Скільки всього прямих утворилося?
3) На скільки частин ці прямі розбивають площину?
Тестові завдання
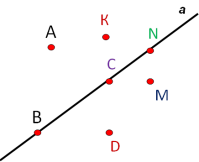 1. Які з точок належать прямій а;
1. Які з точок належать прямій а;
А) А, В, М B) B, C, D, K
C) B, C, N D) A, D, R, M
2. Які з точок не належать прямій а?
А) А, В, М B) B, C, D, K
C) B, C, N D) A, D, К, M
3. На променi MN позначено точку P. Чи може точка M лежати мiж точками N i P? (так/ні)
4. На променi MN позначено точку P. Чи може точка N лежати мiж точками M i P? ? (так/ні)
5. Променi DK i DM —доповняльнi. Яка з точок D, K i M лежить мiж двома iншими?
 A) D; B) K; C) M; D) H.
A) D; B) K; C) M; D) H.
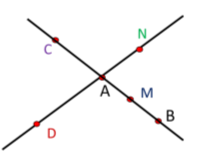
6. Назвіть всі промені з початком у точці М
А) МС; МВ B) МВ; МА; МС
С) МА; MN: MD D) AM; DM; MB


про публікацію авторської розробки
Додати розробку

-

Данилець Вікторія
11.09.2024 в 15:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сидоренко Юлія Ігорівна
06.07.2023 в 10:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kіча Раїса Іванівна
12.09.2022 в 21:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
12.07.2022 в 15:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук