Урок "Геометричний зміст похідної"
Ушаньова Ірина
ліцей хіміко –біологічного профілю
КЗ «Бериславський медичний коледж»
Херсонської обласної ради
Тема уроку: Геометричний зміст похідної
Мета уроку:
- Розглянути з учнями поняття дотичної до графіка функції;
- Встановити геометричний зміст похідної;
- Формувати вміння учнів складати рівняння дотичної до графіка функції в даній точці.
Обладнання: таблиця.
Тип уроку: урок удосконалення знань, умінь і навичок
Хід уроку
І. Організаційний момент.
ІІ. Перевірка домашнього завдання ( здійснюється шляхом збирання учнівських зошитів в кінці уроку).
ІІІ. Актуалізація опорних знань учнів.
- Робота на картках
№1. Користуючись означенням похідної, знайти значення похідної функції 
в точках
Перший учень Другий учень
а)
; 
а)
;
б)
; б)
;
№2. Користуючись означенням, знайти миттєву швидкість точки, яка рухається прямолінійно за законом 
, в момент 
:
Третій учень Четвертий учень
, 
, 
2) Фронтальне опитування
- Що називається похідною функції в даній точці?
- Який алгоритм визначення похідної функції?
- В чому полягає фізичний зміст похідної?
-
Чому дорівнюють похідні функцій
; 
;
; 
; 
?
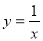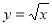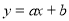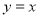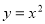ІV. Мотивація навчальної діяльності учнів. Вивчення нового матеріалу. Уявлення про дотичну до кривої дає такий факт: ножицями треба вирізати із картону криволінійну фігуру, тоді ножиці направлені по дотичній до її межі.
Це уявлення про дотичну переведемо на математичну мову.
Наступний матеріал був зазначений на дошці за допомогою таблиці.
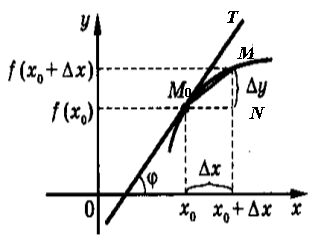Нехай деяка крива є графіком функції 
, а точка 
, яка знаходиться на графіку, має координати 
. Будь-яку пряму 
, де 
– точка кривої 
, відмінна від точки , називають січною до кривої, що проходить через точку . Якщо існує пряма 
, то кут між цією прямою і січною 
прямує до нуля. Як тільки точка 
прямує по кривій 
до точки 
, то її називають дотичною до кривої у точці . Щоб побудувати цю пряму, достатньо знайти кут 
нахилу дотичної до осі 
.
Нехай точка 
(через яку проходить січна 
) має абсцису 
. Коли точка 
, рухаючись по графіку функції
, наближається до точки (це буде при 
) , то величина 
наближається до величини кута 
нахилу дотичної 
до додатнього напрямку осі 
. 
= 
=
, то при 
наближається до 
, тобто 
=
З іншого боку, 
= 
. (1)
Тоді 
= 
.
В рівнянні прямої 
– рівняння дотичної до графіка функції 
у точці 
, 
, тому з (1) 
. Тоді 
Щоб знайти 
, врахуємо, що ця дотична проходить через точку 
. Звідси 
Рівняння дотичної має вигляд:
. Або 
.
Це і є рівняння дотичної до графіка функції 
у точці з абсцисою 
.
Порівняйте вивід формули рівняння дотичної у класі та в підручнику на ст.38 [4].
V. Закріплення нових знань, умінь учнів.
Розв’язуємо усно:
1. Знайдіть значення похідної функції 
в точці 
.
Чому дорівнює тангенс кута нахилу дотичної до графіка даної функції в точці з абсцисою? ( Відповідь: 
).
2. Кутовий коефіцієнт дотичної до графіка функції в точці з абсцисою 
дорівнює 
. Чому дорівнює значення похідної в цій точці? ( Відповідь: 
)
3.Дотична до графіка функції 
у точці з абсцисою утворює з додатним напрямом осі абсцис кут 
. Знайдіть 
( Відповідь: 
).
4. Знайдіть кутовий коефіцієнт дотичної до графіка функції в точці з абсцисою 
а) 
; (2)
б) 
; (3)
в) 
, 
; (0,5)
5. Чи буде дотична до графіка функції 
у точці 
паралельна
прямій:
а) 
; (Ні)
б) 
; (Так)
в) 
; (Ні)
г) 
; (Так).
Задача № 1
Знайти кутовий коефіцієнт дотичної до графіка функції 
в точці 
Розв’язання:
Оскільки кутовий коефіцієнт дотичної до графіка функції дорівнює значенню похідної в даній точці, то 
, 
.
Задача№ 2
Написати рівняння дотичної до кривої 
в точці 
Розв’язання
Загальне рівняння дотичної до кривої 
в точці з абсцисою 
має вигляд: 
Знаходимо: 
; 
, 
;
Отже, 
–шукане рівняння дотичної.
Задача № 3
Знайти рівняння дотичної до графіка функції 
в точці, яка є абсцисою точки перетину прямої 
з віссю абсцис.
Розв’язання
Абсцису точки перетину прямої 
знайдемо з умови 
:
– точка, яка є абсцисою перетину прямої з віссю абсцис.
, 
.
Рівняння дотичної має вигляд:
Відповідь: 
Задача №4
Знайти рівняння дотичної до графіка функції 
, яка паралельна прямій 
Розв’язання
Оскільки за умовою дотична до 
, паралельна прямій 
, то їх кутові коефіцієнти рівні. Знайдемо їх:
, тобто 
.
Рівняння дотичної має вигляд: 
Знаходимо: 
Відповідь: 
Задача №5
Тангенс кута нахилу дотичної до графіка функції 
у точці з абсцисою 
дорівнює 2. Напишіть рівняння дотичної до графіка функції в цій точці, якщо 
( Відповідь:
).
Задача №6
У якій точці параболи 
дотична до неї нахилена до осі
абсцис під кутом 
? ( Відповідь: у точці (2;0) ).
Задача №7
До кривої 
провели дотичну, паралельну осі абсцис. Знайдіть координати точки дотику. (Відповідь: ( 2; – 7)).
Задача №8
Точка рухається прямолінійно за законом 
(
– шлях у метрах, 
– час у секундах). Обчисліть швидкість руху точки:
а) у момент часу ( Відповідь: (6t2–3) (
) );
б) у момент 
( Відповідь: 21
).
Задача №9
Рух точки відбувається за законом 
У який момент часу швидкість руху дорівнює:
а) 
( Відповідь: t=2 );
б) 
( Відповідь:t=5 )
VI. Підсумок уроку:
- засвоїли поняття дотичної до графіка функції в даній точці;
- навчилися визначати кутовий коефіцієнт дотичної, який назвали похідною функції в даній точці;
- навчилися складати рівняння дотичної до графіка функції в даній точці.
VII. Домашнє завдання: опрацювати конспект та текст підручника §3 п.2,6 ст.42 №6(3,4) №8 (2,4) , ст.16 №58, 61
про публікацію авторської розробки
Додати розробку