Тіла обертання. Урок узагальнення та систематизації.

Геометрія

11 клас

 

 

 

 

               

 

 

Автор проекту:   Олізар Ольга Михайлівна

Вчитель математики, вища категорія

«вчитель –методист»

Літківське НВО ім. М.П. Стельмаха

Броварського району

Київської області

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок узагальнення та систематизації знань  з теми «Тіла обертання»

Мета

навчальна: систематизувати та узагальнити знання учнів з теми «Тіла обертання»; підвищити рівень сформованості знань, умінь та навичок розв’язувати задачі з теми; формувати вміння застосовувати набуті знання під час розв’язування практичних задач;

розвивальна: сприяти розвитку систематичних знань, логічного мислення учнів, обчислювальних навиків, математичної мови; розвивати просторове уявлення, уміння спостерігати та аналізувати навколишні явища. Формувати в учнів дослідницькі компетентності, соціальні, саморозвитку і самоосвіти, інформаційні та комунікативні;

виховна: виховувати культуру спілкування, працьовитість, колективізм, відповідальність та вимогливість за виконану справу.

Тип уроку: узагальнення та систематизація знань.

Обладнання: комп’ютер; презентаційні слайди; моделі тіл обертання.

 

Хід уроку

І. Організаційно частина.

Робота по рефлексії настрою та емоційного контакту «Дерево сподівань».

1. З яким настроєм я прийшов на цей урок?

2. Мої очікування від уроку.

Учитель. Намагайтесь щодня для кожної справи знайти якийсь позитивний початок, оскільки від настрою, з яким ви розпочинаєте день або якусь справу, залежать ваші успіхи, а, можливо, і невдачі.

Тож як досягнути успіху? Це запитання постає перед вами практично щодня. Як доречно буде вам у стінах рідної школи  «озброїтися» не лише багажем теоретичних знань і практичних умінь, а й деякими рецептами досягнення успіху.

ІІ. Мотивація навчальної діяльності. Обґрунтування навчання. Виклик.

Учитель. Антична мудрість стверджує «Знання – це сила». На мою думку, знання – це одна із сходинок до успіху в майбутньому. І сьогодні ми будемо плідно працювати, щоб досягнути мети. Отож метою нашого уроку є узагальнення та систематизація знань, умінь та навичок з теми «Тіла обертання».

Клас розділено на групи.

Кожна група підготувала презентацію на тему «Світ навколо нас», де представлено тіла обертання у навколишньому середовищі.

 

 

 

 

 

ІІІ. Актуалізація опорних знань (використовуємо «асоціативний кущ»). Осмислення.

Учитель. Для складання асоціативного куща слід дотримуватися таких правил:

   1. Записати на дошці чи       аркуші в центрі ключове слово (фразу), обвести його (її) колом чи прямокутником.

   2. Записати всі слова (фрази), які спадають на думку.

   3. Після того як заповнені всі можливі «гілки», указати аспекти проблеми, що потребують додаткової інформації.

  4. Поставити знаки питання біля частин куща, в яких є невпевненість.

   5. Записати всі ідеї, які є або скільки дозволяє час.

 Розглянемо блок тіл обертання. Відповіді учнів. Кожне представлення оцінюється по 2 бали

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Усвідомлення змісту

Учитель. Завдання для кожної групи.

1.Встановити залежність. Знайти пари. Правильно з’єднана пара – 1 бал.

 

 

 

1	формула об’єму циліндра		А	V=H
2	формула об’єму конуса		Б	V=R
3	формула об’єму кулі		В	V=H
			Г	V=H
	Відповіді
	1      В	2    А	3     Б

 

Учитель. Завдання для кожної групи. Вибрати по задачі, яка відноситься до назви кожної групи. Розв’язати її. Розв’язок відтворити на дошці.

Правильно розв’язана задача  - 2  бали.

2.   Знайти об’єм равновеликого циліндра, висота якого 8 см.

 А)  64см            Б)  96см          В)  128см         Г)  512см

2. Знайти об’єм конуса, осьовим перерізом якого є рівнобедрений трикутник  з основою 6 см і бічною стороною 5см.

 А)  45см             Б)  36см          В)  15см          Г)  12см

3.                  Площа великого круга кулі дорівнює 36 см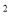. Знайти об’єм кулі.

 А)  216 см          Б) 432см         В) 108 см        Г) 288 см

        

 

Розв’язання задач

 1)      Осьовим перерізом рівновеликого циліндра є квадрат. Оскільки висота циліндра ─ 8 см, то його радіус дорівнює 4 см.

V = RH = ∙4∙8 = 128 ( см) – об’єм циліндра.

 Відповідь:  В) 128 см

           2)     Висота рівнобедреного трикутника є також і медіаною, яка ділить сторону пополам, значить радіус основи циліндра дорівнює 3 см, а його висота – 4 см ( трикутник із сторонами 3, 4, 5 лін. одиниць – єгипетський ).

 V = = ∙3∙4 = 12(см) – об’єм конуса.

Відповідь:  В) 12 см

     3)     Оскільки площа великого круга дорівнює 36см, то R =  36, звідки R = 6см- радіус кулі.  Тоді V = R = ∙6 = = 288( см) – об’єм кулі.

         Відповідь:  В) 288 см

Учитель. Задачі практичного змісту. Зараз ми дізнаємося, як можна застосовувати розрахунки у повсякденному житті для тіл обертання, які нас оточують. Кожна група отримує задачу. Після обговорення та аналізу розв’язку,  біля дошки записати розв’язати задачі.

Задача №1.  Скільки однакових за розміром фаршированих перчин конічної форми може поміститися в 3-літрову ємність циліндричної форми?

Створюємо математичну модель розв’язання задачі.

- об’єм ємності

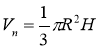- об’єм перцю

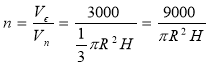- кількість перців

Відповідь: 

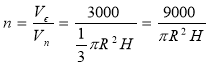
Задача №2.  Що вигідніше: купити кавун радіусом 30см і з’їсти у п’ятьох,чи купити три кавуни діаметром по 20см і поділити на двох?

Розв’язання.

Об’єм кавуна обчислимо за формулою об’єму кулі:

V= 4/3 R³

Об’єм великого кавуна  R=30см  дорівнює

V= 4/3*27000 = 36000 (см³ )

36000  : 5 = 7200 ( см³ ) – кожному.

Об’єм трьох малих кавунів  R=d:2=10 см  дорівнює

V=4/3 1000 = 4000/3 * ( см³ )

4000/3 * : 2= 2000/3*  ( см³ ) – кожному.

Відповідь: один R=30 см.

 

Задача №3.  Відро циліндричної форми вміщує 10 л води. Іграшкове відро має розміри в 10 разів менші. Скільки літрів води вміщує іграшкове відро? 
Розв’язання.

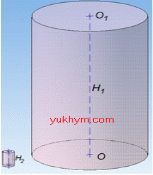
Літр – одиниця вимірювання об'єму (1л = 1дм³). Маємо велике відро з об'ємом V₁=10 л , висотою H₁ та іграшкове відро об'ємом V₂, висотою H2. Оскільки за умовою задачі розміри іграшкового відра в 10 разів менші, то H₁=10H₂ (тобто розміри великого відра в 10 разів більші за іграшкове). 
Всі (прямі) циліндри подібні, а у подібних тіл, за властивістю, відношення об'ємів дорівнює відношенню їх відповідних лінійних розмірів, взятих у кубі, тобто 

 

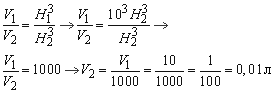
Отже, V₂=0,01 л – об'єм іграшкового відра, тобто кількість води, яку вміщує іграшкове відро. 
Відповідь: 0,01 л – В.

Учитель. Задачі для всього класу. До дошки виходять по представнику від кожної групи і розв’язують задачі. Кожна задача оцінюється у 4 бали.

1. Прямокутний трикутник з  гіпотенузою 20см і гострим кутом 30 обертається навколо більшого катета. Знайти об’єм тіла обертання.

Розв’язання

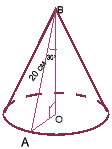  Нехай на малюнку зображено конус, який утворюється від  обертання прямокутного трикутника АОВ ( АОВ =90) навколо більшого катета ВО, у якому гіпотенуза АВ = 20 см, а  АВО =30.

 У прямокутному трикутнику катет, який лежить проти кута 30, дорівнює половині гіпотенузи, значить R = = 10(см) – радіус основи конуса. За співвідношеннями у прямокутному трикутнику H =  R∙ctg 30 = 10(см) ─ висота конуса. Тоді V = = = (см) ─ об’єм конуса.

  Відповідь:     см

2. Діагональ осьового перерізу циліндра дорівнює т і утворює з площиною основи кут β .        Знайти об’єм циліндра.

 

  Розв’язання

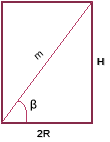 Нехай на малюнку зображено осьовий переріз циліндра, діагональ якого дорівнює т, а кут,який утворює ця діагональ з діаметром основи дорівнює . Із прямокутного трикутника знайдемо висоту циліндра та його діаметр: H = т, d = 2r = т, звідки

 r = т, тоді  V = = т· т= тSin  = тSin2Cos( куб. од.) ─ об’єм циліндра.

   Відповідь: т Sin2Cos куб. од.

Учитель. Експрес опитування  (інтелектуальна розминка) - результати відповідей оцінюються по 1б.,

Опитування проводиться у формі брейн-рингу, якщо члени групи помиляються або не знають відповіді, то на це запитання можуть відповісти  інші групи

А. Циліндр.

1. Яке геометричне тіло називається циліндром?

2. Внаслідок обертання якої геометричної фігури утворюється циліндр?

3.  Що є елементами циліндра?

4. Які існують види перерізів циліндра?

5. Чому дорівнює об’єм циліндра?

Б. Конус.

1. Яке геометричне тіло називається конусом?

2. Внаслідок обертання якої  геометричної фігури утворюється конус?

3. Що є елементами конуса?

4. Види перерізів конуса?

5. Чому дорівнює об’єм конуса?

В. Куля.

1. Яке геометричне тіло називається кулею; сферою?

2. Внаслідок обертання якої геометричної фігури утворюється куля, сфера?

3. Що є елементами кулі?

4. Які існують перерізи кулі?

5. Чому дорівнює об’єм кулі?

 

ІV. Узагальнення та систематизація знань, умінь, навичок.

На цьому етапі учні кожної групи розв’язують тестові задачі:

Учитель. Математичний двобій «мозковий штурм». Тестові завдання  з вибором однієї правильної відповіді отримує кожна група.  Учні розв’язують кожний по одній задачі, але всі задачі повинні бути розв’язані. Задачі оцінюються по 2 бали.

Перевірка відповідей.

«Математичний двобій»

1.               Об’єми циліндрів відносяться як 27 : 64. Як відносяться їх радіуси?                        а) 9 : 16                        б) 27 : 64                           в) 3:4
2.               У скільки разів збільшиться поверхня кулі, якщо її об’єм збільшити у 3 рази?

а) 6 р.                              б) 9 р.                            в) 3 р.

3.  У циліндра і конуса однакові висота і радіус. Яке тіло має більший об’єм?

а) конус                          б) циліндр                    в) рівні об’єми.

4. У циліндричній посудині рівень води перебуває на висоті 20 см. На якій висоті перебуватиме рівень води в циліндричній посудині, радіус якої у 2 рази більший від радіуса першої?

а) 10 см                           б) 4 см                           в) 5 см 

5. Свинцеву кулю радіусом 5 см переплавили у кульки, радіус яких 1 см. Скільки таких кульок одержали?

а) 25 б) 125 в) 5

6. Усі розміри дитячого відерця у 10 разів менші, ніж відра місткістю 12 літрів. Скільки води поміститься в дитяче відерце?

а) 12 см³                           б) 1,2 л                         в) 0,12 см³

7. Твірна конуса 10 см, а висоти 8 см. Знайти S площу бічної поверхні?

а) 30π      б) 10π      в) 60π

8. Осьовий переріз циліндра – квадрат, діагональ якого дорівнює 10 см. Знайти площу бічної поверхні.

а) 10π     б) 100π   в) 40π

9. Радіус кулі дорівнює 10 см; її пертнули січною площиною на відстані 8 см від центра кулі. Знайти довжину великого кола.

а) 10π    б) 20π   в) 16π

 

Учитель.  Властивості тіл обертання, площі їх поверхонь та об’єми здавна мали важливе значення  не тільки в геометрії, але й у житті людини, у різноманітних царинах людської діяльності.

Кожна група отримує прикладні задачі (4 б.). Із кожної групи один учень захищає свою задачу.

Кожна група отримує по хокейній шайбі різного розміру. Потрібно обчислити її об'єм , зробивши відповідні заміри.

Після виконання всіх завдань, кожен учень класу отримує картки і заповнює їх.

 Застосування набутих компетентностей. Учні заповнюють картку.

Що ми знаємо	Що хочемо знати	Що ми вивчили

Підсумок уроку.

Учитель.  Існує 3 види тіл обертання. На закріплення своїх знань колективно розв’яжемо кросворд

Тіла обертання

		1   1						9
2								3
					8
	4									10
								5
								6
									7

По горизонталі:

1. Як називається тіло, яке складається з двох кругів, що не лежать в одній площині й поєднуються паралельним переносом? (Циліндр)
2. Яку фігуру одержимо, якщо обертати прямий трикутник навколо його катета? (Коннус)
3. Як називається відрізок, який з'єднує дві точ­ки кульової поверхні і проходить через центр? (Діаметр)
4. Який це циліндр, якщо його твірні перпенди­кулярні до основи? (Прямий)
5. Як називається межа кулі? (Сфера)
6. Яке тіло складається з усіх точок простору, що знаходяться на відстані, не більшої за да­ну, від даної точки? (Куля)
7. Як називається пряма, яка проходить через висоту тіла обертання? (Вісь)

По вертикалі:

1. Як називається точка, від якої відсторонені всі точки простору на однаковій відстані? (Центр)

8. Як у циліндра називається відстань між осно­вами? (Висота)

9. Як називається відрізок, який сполучає будь- яку точку кола з його центром? (Радіус)

10. Через будь-яку точку кульової поверхні скільки можна провести дотичних? (Безліч)

Домашнє завдання.

   Учитель. Працюючи разом, маючи поряд надійних партнерів, ми досягли певного успіху. Але в житті і в навчанні часто для досягнення повного успіху треба вміти працювати без допомоги, повністю самостійно. Тому продовжувати працювати над розв’язанням задач ви будете вдома. 

Рівень ( бали)	Домашнє завдання
1 -3	Обчислити  об’єм звичайного лимона.
4-8	Об’єм конуса дорівнює 32. Обчисліть висоту конуса, якщо радіус його основи дорівнює 4 см.
9-12	Об’єм циліндра дорівнює 200 , а його висота ─ 8см. Обчисліть довжину основи кола циліндра.

 

 Рефлексія.

Самоаналіз уроку учнями.

Учитель.

•                   Чи вдалося нам  з вами  отримати очікувані результати, якщо - ні,  то - чому?
•                   Над чим, ви вважаєте, нам потрібно попрацювати на наступному уроці?
•                   Які проблеми залишилися невирішеними на вашу думку?

Щоб відповісти на ці та інші запитання, перейдемо до самоаналізу уроку.

    Зараз саме час повернутися до початку нашого уроку, до мети, яку ми перед собою ставили. На мою думку, ми з вами досягли нашої мети – повторили теоретичні знання  та способи їх розв’язання, систематизували та узагальнили свої навчальні вміння та навички. Залишається різносторонньо проаналізувати ситуацію уроку. Взагалі, вміння аналізувати є дуже важливим у наш інформаційний час. Людиною, яка вміє аналізувати, практично неможливо маніпулювати, вона завжди знайде вихід з будь-якої ситуації.

(Виступ кожного учня групи – відповідь на одне із запитань) Починати свою відповідь можна, як завжди словами:

•                               цей урок познайомив мене…
•                               цей урок навчив мене…
•                               цей урок допоміг мені…
•                               на мою думку цей урок сприяв розвитку 

 

Учні  заповнюють дерево очікування.