Урок-гра "Вектори на площині"
Перевірити і узагальнити знання учнів з теми "Вектори на площині", стимулювати пізнавальну діяльність, розвивати інтерес до предмета, формувати вміння швидко та чітко формувати свої думки і логічно викладати їх; виховувати наполегливість у навчанні.
Матеріал містить конспект уроку та презентацію.

Мета: «Перевірити і узагальнити знання учнів з теми, стимулювати пізнавальну діяльність, розвивати інтерес до предмета, формувати вміння швидко та чітко формувати свої думки і логічно викладати їх; виховувати наполегливість у навчанні.
Тип уроку: Узагальнення та систематизації знань
Обладнання: Проектор, комп’ютер, мобільні телефони
Епіграф: Навіть якщо математика не навчить нас
додавати любов і віднімати ненависть,
вона прищеплює віру в те,
що для кожної задачі є вирішення
Хід уроку.
Організація класу.
Доброго дня, діти! Сьогодні ми узагальнимо наші знання про вектор, його координати, довжину, скалярний добуток, колінеарність векторів. А урок у нас буде не зовсім звичайний урок, урок-гра.
Епіграфом до нашого уроку я підібрала такі слова:
Навіть якщо математика не навчить нас
додавати любов і віднімати ненависть,
вона прищеплює віру в те,
що для кожної задачі є вирішення.
Так і в житті немає проблем, які не розв’язуються, є люди, які не хочуть або не вміють це робити
Я об’єднала вас у команди. Ви мали вибрати капітана, придумати назву та девіз.
То ж капітани представляйте свої команди.
(представлення команд)
Правила гри:
Практика без теорії – сліпа, а теорія без практики – мертва.
То ж наша гра матиме два тури: «Хай живе теорія» та «Її величність практика»
У першому турі команди виконують тести по теорії з теми "Вектори на площині"
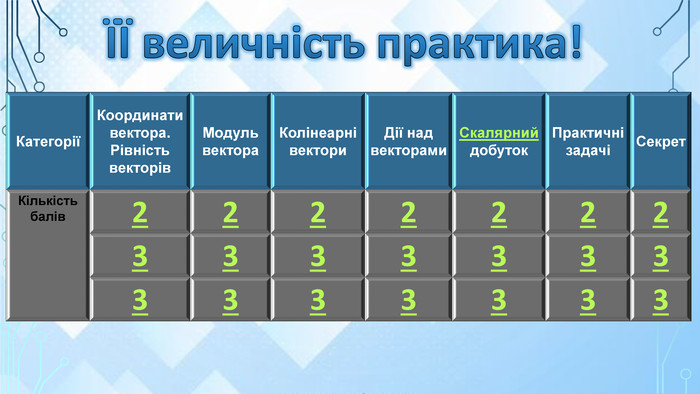
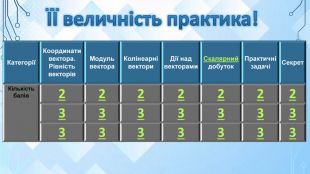
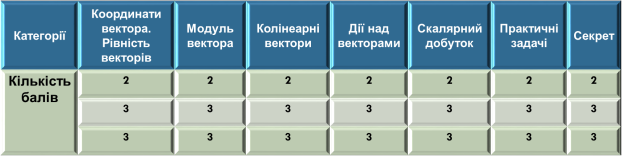
У другому турі командам пропонується 7 тем. Кожна тема складається з 3
запитань, які різняться за складністю. Перше запитання «коштує» 2бал, друге — 3, третє — 3.
Команди по черзі вибирають теми і «вартість» завдання. Капітан називає учасника, який роз’язуватиме завдання, якщо ж учасник не може впоратись, то команда може допомогти. За правильну відповідь на запитання команда отримує ту кількість балів, скільки «вартує» запитання.
Якщо ж команда не знає розв’язання завдання, то інша команда може їм допомогти, чим заробить собі бал.
Після останнього питання відбувається підрахунок балів кожної
команди. Якщо у двох або більше команд однакова кількість балів, то
переможець визначається за додатковими показниками (кількість
правильних відповідей, сума правильних відповідей тощо).
I тур
Хай живе теорія!
Командам на телефони вчитель розсилає тести. На їх виконання дається 5хв. Результат відображається на дошці
https://docs.google.com/forms/d/14ztI2hbuVHcCjnGD3rcxeIRVe3__lPzgSogMJfSq8wc/edit
(підсумки за результатами I туру)
Пам´ятайте! Якщо ви хочете навчитися плавати, то сміливо заходьте у воду, а якщо хочете навчитися розв´язувати задачі, то розв´язуйте їх!
II тур
ЇЇ величність практика!
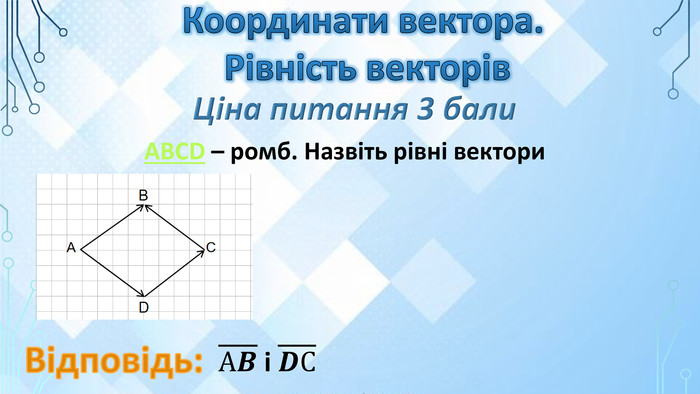
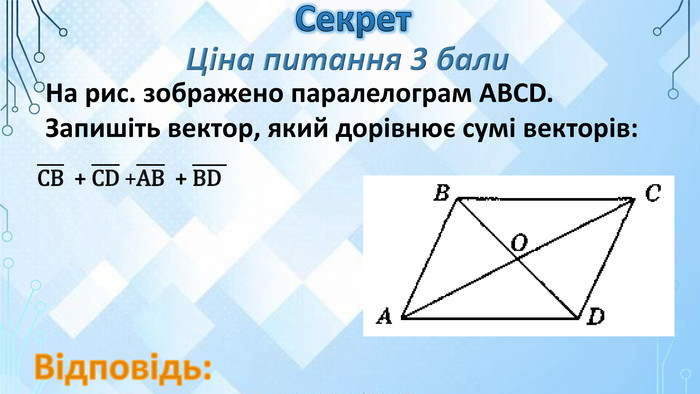
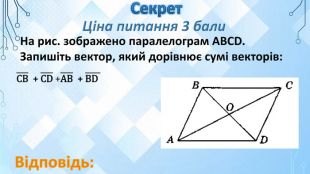
Команди по черзі, вибирають завдання і розв’язують.
Після останнього питання журі підраховує бали
Поки журі підраховує бали
Історична довідка про вектори.
«Термін «вектор» (від латинського vector -« несучий ») вперше з'явився в 1845 році в ірландського математика Вільяма Гамільтона (1805-1865) у працях з побудови числових систем. Поняття вектор виникає там, де доводиться мати справу з об'єктами, які характеризуються величиною і напрямком: наприклад, швидкість, сила, прискорення. Це поняття було охоче сприйняте багатьма математиками і фізиками. У сучасній математиці воно відіграє найважливішу роль. Вектори застосовуються в класичній механіці, квантовій фізиці, в математичній економіці та інших багатьох розділах природознавства і різних областях математики ».
Інтерактивна вправа
«Не хочу хвалитися, але я…»
Найкраще я засвоїв …
Добре знаю …
Добре вмію …
Вмію розв'язувати …
Вмію знаходити …
Найкраще мені вдається…
Підбиття підсумків уроку. Виставлення оцінок.
Домашнє завдання.

про публікацію авторської розробки
Додати розробку