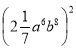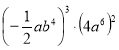Урок – гра з теми «Систематизація та узагальнення знань за І семестр»

Пояснювальна записка. Правила математичної каруселі

 Використано: http://matholymp.com.ua/pravila-matematichnoi-karuseli/

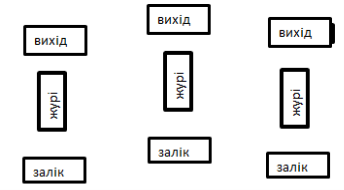 Математична карусель — командне змагання. Кожна команда має в своєму складі 5-7 гравців (зазвичай, це три команди). Частина учасників команди під час каруселі перебуває на так званому вихідному рубежі, решта команди — на заліковому рубежі. Поки змагання триває, деякі учасники переходять з початкового рубежу на заліковий, а інколи навпаки. Учасники, що перебувають на різних рубежах, не повинні спілкуватися між собою. Тому зазвичай гравців початкового та  залікового рубежу розміщують на деякій відстані від- стані один від одного.

Спершу всі гравці команди розташовуються на вихідному рубежі в певному порядку — від учасника № 1 до учасника № 6. Порядок/нумерацію учасників команда визначає сама перед початком каруселі. За сигналом початку змагання кожній команді на картці видають першу задачу. Коли команда розв’язала задачу, вона пише відповідь до неї (лише відповідь — повне розв’язання і доведення наводити не треба). Папірець команда повертає члену журі, який перевіряє відповідь. Якщо відповідь неправильна, нічого не відбувається, команда просто отримує наступну задачу. Якщо відповідь правильна, один з членів команди — № 1 — переходить із вихідного рубежу на заліковий.

Далі гравці на початковому й заліковому рубежах працюють незалежно. Й тим, й іншим видають щоразу нові задачі. Якщо гравці вихідного рубежу надали правильну відповідь до чергової задачі, один із них — той, хто був першим у черзі — переходить на заліковий рубіж (і сідає в кінець черги залікового рубежу). Якщо ж гравці залікового рубежу дали неправильну відповідь, той гравець, хто був першим у черзі залікового рубежу, переходить назад на початковий рубіж (і сідає в кінець черги початкового рубежу). Таким чином, гравці команди переміщуються між початковим і заліковим рубежами в спосіб, що нагадує катання на каруселі. Якщо на початковому рубежі до задачі дається неправильна відповідь, або на заліковому – правильна, всі гравці залишаються на своїх місцях.

Суттєва різниця між вихідним і заліковим рубежами полягає в тому, що за правильну відповідь задачі на заліковому рубежі команда отримує в свій залік певні бали, якщо ж надана правильна відповідь задачі на початковому рубежі, то єдина користь для команди — можливість відрядити ще одного учасника на заліковий рубіж. Бали на заліковому рубежі нараховують у такий спосіб: за першу правильну відповідь дають 3 бали, за другу — 4, і за кожну наступну на бал більше, ніж за попередню. Ланцюжок, однак, обривається, коли на якусь із задач була дана невірна відповідь. Тоді за наступну задачу, якщо на неї буде дана правильна відповідь, команда отримує 5 очок, якщо ця (на яку дали неправильну відповідь), коштувала 6 очок або більше; 4 бали, якщо ця коштувала 5; 3 бали, якщо ця коштувала 4 або 3 бали. Ціна наступних задач знов зростає на 1 (поки команда дає на них правильні відповіді). Таким чином, після ланцюжка з шести правильних відповідей, однієї неправильної та ще трьох правильних відповідей команда отримає 3 + 4 + 5 + 6 + 7 + 8 + 0 + 5 + 6 + 7 балів, а після серії з чотирьох правильних відповідей, двох неправильних і ще однієї правильної відповіді на задачі 3 + 4 + 5 + 6 + 0 + 0 + 4 бали (зауважте: за останню задачу команді нарахували 4 бали, бо попередня, шоста, задача коштувала 5 балів).

Нову задачу гравцям на певному рубежі видають тоді, коли вони дали відповідь (правильну або неправильну) до попередньої задачі. Якщо команда на рубежі не в змозі розв’язати ту чи іншу задачу, вона може зробити відмову. Тоді бал за наступну задачу не знижується (таких відмов може бути мінімум або й зовсім відсутні).

Задачі видаються в порядку, спільному для всіх команд.

Кількість задач на обох рубежах обмежена. Задачі для початкового й для залікового рубежів різні. Гра вважається закінченою для команди, якщо

1. закінчився час гри;
2. закінчилися задачі на заліковому рубежі;
3. закінчилися задачі на вихідному рубежі, а на заліковому немає жодного гравця.

Гра закінчується коли вона закінчилася для всіх команд. Час гри, кількість вихідних та залікових задач та відмов заздалегідь обумовлюються.

Результат команди — це сума очок, які вона отримала за правильно розв’язані на заліковому рубежі задачі.

Поки карусель триває, ведуть її протокол: записують бали, що отримала кожна команда за кожну із задач залікового рубежу Це робиться  безпосередньо на дошці. Кожен член команди повинен мати змогу дізнатися про проміжні результати. За певний час до завершення гри оновлювання протоколу можуть припинити (що інколи позитивно впливає на мотивацію команд, які мають суттєвий відрив від лідера).