Урок "Корінь n-го степеня. Арифметичний квадратний корінь"

Корінь n-го степеня. Арифметичний квадратний корінь

Мета уроку: сформувати  в учнів уміння перетворювати  радикали: вносити множини під знак радикала, виносити множник з-під знаку радикала, звільнятися від ірраціональності в знаменнику дробу, зводити подібні радикали.

Обладнання: роздавальний матеріал ( умови тесту).

Тип уроку: формування вмінь і відпрацьовування навичок

ХІД УРОКУ

І. Організаційний  етап

ІІ. Перевірка домашнього завдання

 Учні самостійно перевіряють правильність виконання домашнього завдання за зразком, який учитель заздалегідь підготував на дошці. Потім виконується тестове завдання з наступною взаємною перевіркою.

Тест

Зазначте правильну відповідь.

Варіант 1

1. Розв’яжіть рівняння х⁴ = 16

А 2       Б  -2      В 4    Г

2. Знайдіть значення виразу

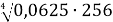
А 80       Б  2      В 8    Г 4

3. Знайдіть значення виразу           

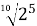
      А        Б        В 4    Г 2

4. Обчисліть:

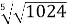
      А        Б        В  32   Г 2

5. Спростіть вираз 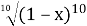, якщо х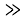1

А 1 - х       Б       В  х - 1   Г

6. Обчисліть 

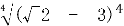
А        Б   - 3      В  3 -            Г

 

 

 

 Варіант 2

1. Розв’яжіть рівняння х ⁴ = 81

       А  - 3      Б  ± 3        В  9      Г 3

2. Знайдіть значення виразу

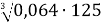
А  20      Б  8      В  40       Г 2

3. Знайдіть значення виразу           

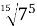
А   7    Б         В               Г 3 

4. Обчисліть

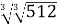
А       Б         В         Г 2

5. Спростіть вираз 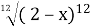, якщо х

А   х - 2    Б  2 - х    В         Г

6. Обчисліть

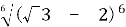
А       Б         В   2 -      Г

Відповіді до тестового завдання

Варіант 1   1 Г    2 Б   3 А    4 Г   5 В   6 В

Варіант 2   1 Б    2 Г    3 В    4 Г   5 А   6 В

ІІІ. Актуалізація опорних знань учнів

Завдання класу

1. Винесіть множник з-під знака квадратного кореня:

а)             б)

     2. Внесіть множник під знак квадратного кореня:

     а)  5;     б) х, якщо х 0;  в)  х, якщо х.

     3. Звільніться  від ірраціональності в  знаменнику дробу:

     а) ;       б) .

     4. Спростіть вираз:

     а) 7 – 2 ;       б)  ( – 1)² .

     5. Які формули було використано в ході виконання завдань 3 і 4?

   6. Заповніть пропуски, щоб одержати формулу суми кубів ( або формулу різниці кубів):

  а) ( х – 2) (…+ …+ 4) = … - …;    б) 27 – х³ = (… - х) ( 9+…+ …).

IV. Формулювання теми, мети й завдань уроку.

      Мотивація навчальної діяльності учнів

V.  Формування вмінь і відпрацьовування навичок.

Винесення множника з-під знака радикала:

Внесення множника під знак радикала.

Учитель наводить приклади, в яких показує, як, використовуючи властивості кореня n-го степеня, можна виконати перетворення винесення множника з-під радикала та перетворення внесення множника  під знак радикала. Потім виконуються аналогічні вправи: одна ( а ) – з розбиранням біля дошки,  друга (б) – самостійно. Один з учнів працює за відкидною дошкою. Після закінчення роботи  він відкриває своє розв’язання, щоб учні могли звірити з ним виконане самостійно завдання.

1. Винесіть множник з-під знака радикала:

а) ;      б)

     2. Внесіть множник  під знак радикала:

       а)    3 ;          б) 2

 Поняття подібних радикалів

Учитель пояснює, які радикали називаються подібними, наводить приклади.

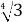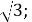
1. Серед даних радикалів виберіть подібні: 8; ;  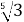0,3 .
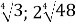2. Обчисліть: 5 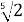 - 2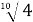 + 3 .
3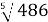. Обчисліть: 2 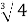+ 3 - 

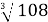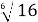
 Порівняння  радикалів.

Учитель розповідає класу, що для порівняння радикалів використовують твердження; якщо а, тобто  більшому підкореневому виразу відповідає  більше значення кореня.  Таким чином, для порівняння радикалів досить звести  всі радикали  до одного показника кореня й урахувати  вищезазначену  властивість.

1. Порівняйте 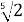  і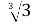

Розв’язання

1. Запишемо корен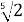і    і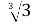 у вигляді  коренів з однаковими показниками: 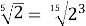= 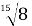;  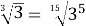= . Відповідно до визначеного  твердження    
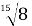
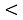
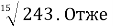
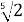
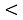
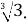
2. Порівняйте  числа:

  і ;        б) і .

Ірраціональність у знаменнику дробу

1. Звільніться від ірраціональності у знаменнику дробу;

а) ;     б) ;    в) .

 2.   Звільніться від ірраціональності у знаменнику дробу:

      а) ;         б) ;

VI.  Підбиття підсумків уроку

Учитель ще раз нагадує учням, які радикали називають подібними, як ввести множник під знак кореня, винести множник з-під знака кореня, звільнитися від ірраціональності в знаменнику дробу, як порівнювати радикали.

VIІ. Домашнє завдання

Виконати вправи.

1. Винесіть множник з-під знака кореня:

        а)

        б) ;

        в) х³у⁷, якщо у 0.

 

2. Внесіть  множник під знак кореня:

а) m²$

б) ху ;  якщо у 0.

в) х³у⁷ , якщо х 0; у 0.

 

3. Порівняйте числа

          а) і  ;    б)   і ;   в) і  .

 

4. Звільніться від ірраціональності в знаменнику дробу:

     а) ;      б) ;

в)