Урок "Куля, описана навколо піраміди", 11 клас, профільний рівень

                       Тема :           Куля, описана навколо піраміди .

 

                    Мета : сформувати в учнів уміння знаходити центр кулі,

                                 описаної навколо піраміди , розвивати просторову уяву ,                          

                                  логічне мислення.

                                                  Хід уроку :

1. Актуалізація  опорних знань .

а) Перевірка домашнього завдання ;

б) Фронтальне опитування .

1) Навколо яких многокутників можна описати коло ?

2) В які многокутники можна вписати коло ?

3) В які призми можна вписати кулю ?

4) Де знаходиться центр кулі вписаної в призму ?

5) Навколо яких призм можна описати кулю ?

6) Де знаходиться центр описаної кулі ?

в) Розв’язування задач за готовими малюнками ( усно ) .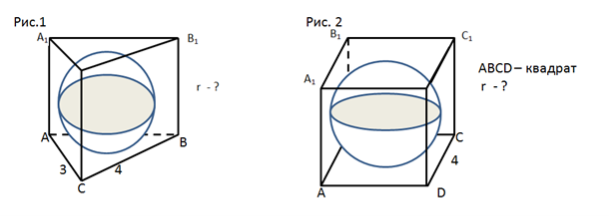

 

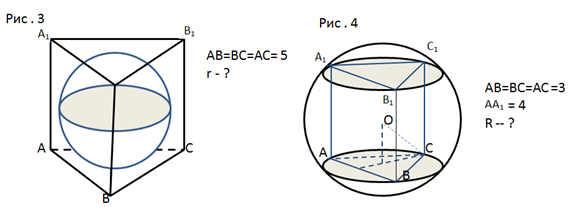
2. Сприйняття та усвідомлення нового матеріалу .

Куля називається описаною навколо піраміди , якщо всі вершини піраміди лежать на кулі . Центр кулі - це точка рівновіддалена від усіх вершин піраміди .

Розглянемо піраміду , в якій основою висоти є центр описаного  навколо основи кола .

Задача 1. Бічне ребро правильної чотирикутної піраміди дорівнює b і утворює з висотою кут . Знайти площу поверхні

сфери описаної навколо піраміди .

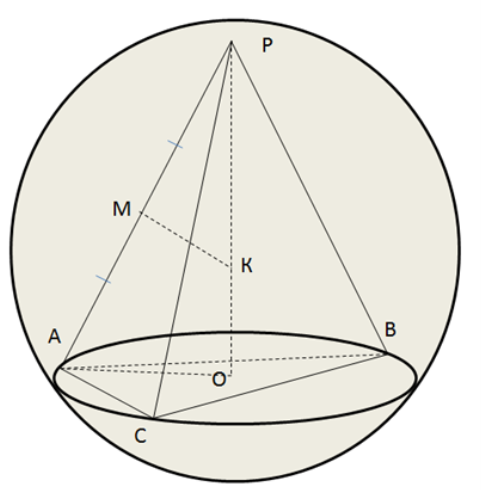
Розв’язання .

РАВС – правильна піраміда , то центр описаної кулі лежить на прямій , що містить висоту РО .

У площині РОС проведемо серединний перпендикуляр МК до бічного ребра РС , МК РО = К .

Отже , т. К – центр описаної кулі ,

 РК – її радіус .

           У  РМК : РМ=  ,                РК = ,  R = PK .

            S =4,   S = .

            Відповідь : .

На мультимедійній дошці висвітлюється інший спосіб розв”язання цієї задачі. Наголошується , що при розв”язанні  таким способом кулю креслити не обов”язково , що демонструється далі.

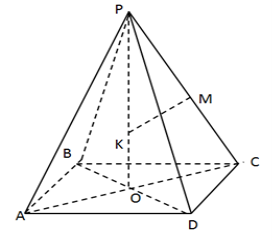
Задача 2. У правильній чотирикутній піраміді сторона основи дорівнює а , плоский кут при вершині – . Знайти радіус описаної кулі.

 Розв”язання.

 

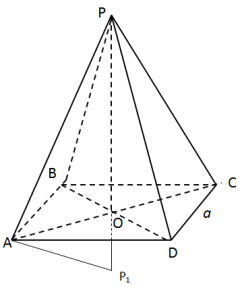
Піраміда правильна , центр описаної кулі лежить на прямій , що містить висоту.

Продовжимо висоту РО до діаметра РР₁= 2R ,  тоді РАР₁= 90⁰.

 

 

1. У DPC : РС =   ;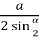

У РОС : РО = ; РО = = ,

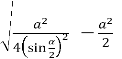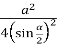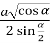2. У РАР₁ :      РА²= РО^.РО₁ ;                  = ^{. 2R ,}

Звідси , R = .

Відповідь :  .

 

Задача 3. В основі піраміди лежить трикутник з кутами та і площею S . Всі бічні ребра піраміди утворюють з висотою

кут . Визначити поверхню сфери описаної навколо піраміди.

 

Розв’язання .

Нехай РАВС – задана піраміда S_ABC = S , CAB = ,

ABC =APO = BPO = CPO = .

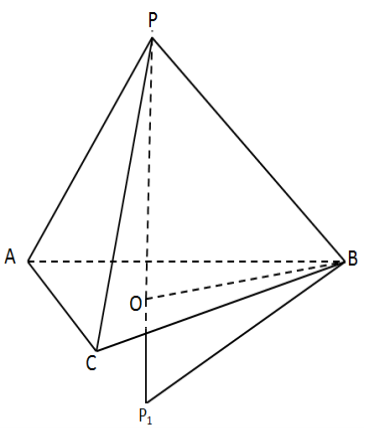Поверхня сфери :   S_k =4, де R –радіус кулі

 

1.               Оскільки ребра піраміди створюють рівні кути з її висотою , то основою висоти піраміди є центр описаного навколо основи кола,  отже, центр cфери, описаної навколо піраміди лежить на прямій ,

що містить висоту РО піраміди.

Продовжимо висоту РО до діаметра РР₁ =2R ,тоді  РВР₁ = 90⁰ .

2.У РВР₁ : РВ = 2R ,

ОВ = 2R=R,

За наслідком з теореми синусів для трикутника АВС , маємо :

= =2ОВ =2R ,звідки АС=2R,

BC= 2R ,

S_ABC = AC^.ВС^.sin(180⁰- ),

 S_ABC = 2R²sin²2sinsinsin();

Отже ,  R² = .

2.    S_k = .

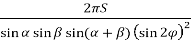Відповідь : .

 

 

Задача 4. У кулю радіуса R вписано правильну трикутну піраміду, бічні

грані якої нахилені під кутом до основи .Знайти площу повної

поверхні піраміди.

Розв’язання.                                        

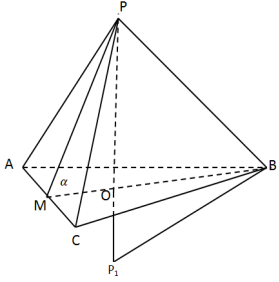
1.Куля описана навколо правильної піраміди, її центр лежить на прямій РО, РР₁=2R, оскільки ОМ АС ,то РМАС і РМО= .

2.Нехай АВ=а.    S_пп = S_о+S_б ,     S_o= ,                S_б = ;

                               S_пп= .

3.У РОМ :           РО= ;

   У РВР₁ :            ОВ² = РО^.Р₁О , ОВ = , РО = , Р₁О = 2R - ;

Звідки ,  a = ,     

S_пп =.

Відповідь : .

 

Задача 5. В основі піраміди лежить прямокутник , у якого кут між діагоналями . Одне бічне ребро піраміди перпендикулярне до площини основи , а найбільше її бічне ребро нахилене до основи під кутом . Радіус описаної навколо піраміди сфери дорівнює R. Знайдіть висоту піраміди та площу її основи.

Розв’язання .

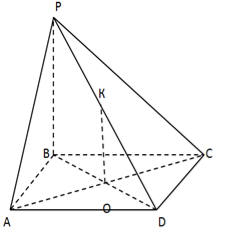1.У площині РВD проведемо ОКРВ.

   РВ(АВС), ОКРВ, тому  ОК(АВС).

Оскільки т.О є центр описаного навколо основи кола і  ОК (АВС), то кожна точка прямої ОК  рівновіддалена від вершин основи.

У РВС :  ОВ = ОD ,ОМРВ, тому РК = КD.

Отже , точка К  рівновіддалена від усіх вершин піраміди, а тому є

центром описаної кулі, РК = КD= R.

2. УРВD: РВ = РD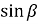, PB = 2R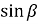,    BD = PD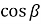,BD = 2R,

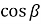    S_o = BD²,            S_o = R².

Відповідь : 2R ; R² .

3.Підведення  підсумків уроку.

4.Домашнє завдання: А.Г.Мерзляк Геометрія 11, профільний рівень, пункти 11, 12;

№11.21; 11.26; 11.28.

 

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

           КУЛЯ ОПИСАНА НАВКОЛО ПІРАМІДИ