Тема: Кут. Види кутів.

Мета: Сформувати уявлення учнів про кути. Сформувати знання учнів про елементи кута, позначення кутів. Формувати уміння пояснювати, що таке кут, позначати кути. Сформувати розуміння учнями поняття рівних кутів, більшого чи меншого кута. Сформувати уміння класифікувати кути. Сприяти розвитку логічного та критичного мислення, просторової уяви учнів. 

Тип уроку: засвоєння нових знань, умінь і навичок.

Хід уроку І. Організаційний момент.

ІІ. Перевірка домашнього завдання. 

Доповнити записи:

1)      (х+358) - 459=126              х+358=459____126             х+358=____            х= _____ - 358           х= _____

2)      951 – (х – 354)=882 х – 354= 951 ____ 882 х – 354= ____ х=354 + ____ х= ____

ІІІ. Актуалізація опорних знань.

Назвіть фігури, які ви бачите на рисунку. Що ви знаєте про ці фігури?

А                        В

О                                                         М

     а

ІV. Оголошення теми уроку. 

Сьогодні ми познайомимося ще з однією геометричною фігурою. Це кут. Дізнаємося, які бувають кути. Тема нашого уроку «Кут. Види кутів.» V. Формування нових знань.

1.  Проведемо два промені зі спільним початком. Це промені ВА і ВС. Утворилася фігура, яка називається кутом. 

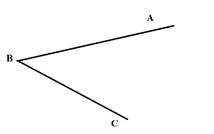
Точка В називається вершиною кута. Промені ВА і ВС - сторонами кута. 

Цей кут  можна позначити так:          АВС або         СВА, але не можна        ВАС чи        ВСА. Буква, що позначає вершину пишеться посередині. Кут можна позначити і однією буквою – назвою його вершини. В нашому випадку це       В.

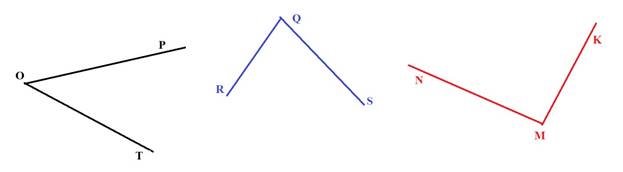
Вправа.Назвіть кути, що ви бачите на рисунку.

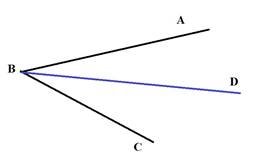
2.  Проведемо промінь ВD між сторонами кута АВС. Тоді маємо три кути, жоден з яких не можна позначити однією буквою, а лише трьома. Наприклад це кути АВС, АВD, DВС

3.  Ми з вами знаємо, що можна порівнювати відрізки. Чи можна порівнювати кути? 

У мене є два кути. Якщо їх можна накласти один на один, сумістивши вершини, так, щоб вони співпали, то такі кути називаються рівними.

(показати моделі)

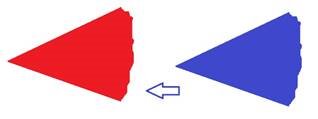
Два кути називаються рівними, якщо вони суміщаються при накладанні. 

Рівні кути позначають рівною кількістю дужок.

А тепер візьмемо два не рівні кути. Цікаво, який з них більший? Накладемо їх один на один, сумістивши вершини і одну зі сторін. (Учні роблять висновок).

4.  Побудуємо кут, сторони якого утворюють пряму. Такий кут називається розгорнутим.

Якщо аркуш паперу, на якому побудовано розгорнутий кут скласти так, щоб сторони цього кута співпали, то отримаємо два рівні кути. Кожен з них називається прямим кутом.

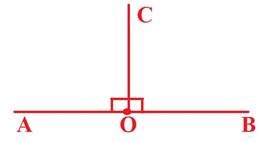
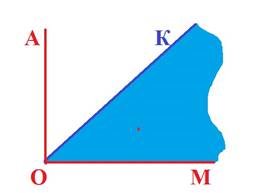
Кут менший від прямого називається гострим. На рисунку кут КОМ гострий.

Кут більший від прямого, але менший від розгорнутого називається тупим. Кут СОВ на рисунку – тупий.

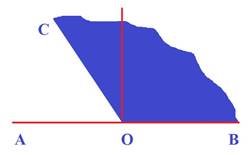
Вправа. Визначте вид кута на рисунку.

VІ. Формування нових вмінь.

1.                   Робота з підручником. Вправи №286, №291. (Підручник «Математика 5клас. Мерзляк, Полонський, Якір)

2.                   Практичне завдання. Побудувати гострий кут АСВ, прямий кут MNR, тупий кут QLS, розгорнутий кут DKF. Запишіть, як ще можна позначити ці кути.

VІІ. Підведення підсумків уроку.

1)      Що ви дізналися нового на уроці?

2)      Що таке кут?

3)      Які бувають кути?

4)      Як можна позначати кути?

5)      Визначте чи правильно позначено кути, зображені на рисунку?

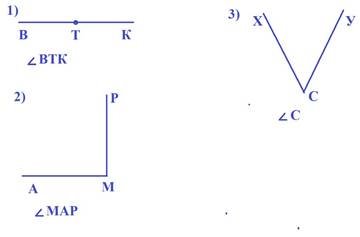
VІІІ. Домашнє завдання. Виконати вправи№287, №292