Урок "Кут. Вимірювання та відкладання кутів"
Тема: Елементарні геометричні фігури та їх властивості
Урок 4
Кут. Вимірювання та відкладання кутів.
Мета заняття:
- повторити, узагальнити і систематизувати знання учнів щодо означення елементів та видів кутів, а також про властивість вимірювання кутів;
- доповнити знання новим поняттям «внутрішньої області кута»;
- виробити вміння виконувати зображення кутів певної градусної міри і позначати зображені кути;
- з'ясовувати питання відкладання кутів.

«Коли я розпочав наукове вивчення геометрії, всі факти, які я мав вивчати, були, власне, мені добре відомі... новим для мене був строгий метод науки, і я за допомогою цього методу відчув, що зникають ті труднощі, які заважали мені в інших галузях.»
Герцен О. І.
Герцен О. І. – письменник, філософ, педагог.
Методичні рекомендації:
Дана тема рекомендована для тих учнів, які мають намір самостійно вивчити і опрацювати тему «Кут. Вимірювання та відкладання кутів», з подальшим розв’язанням практичних завдань. Ознайомитись з новими одиницями вимірювання кутів: мінута і секунда.
Тема та структура матеріалу повністю відповідають навчальній програмі з математики за курс базової школи.
Матеріали до уроку
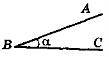
Означення: Кут — це геометрична фігура, яка складається з двох променів, що виходять з однієї точки.
Промені називають сторонами кута, а їх спільний початок — вершиною кута.
Кут з вершиною O і сторонами OA і OB. Такий кут можна назвати по‑різному: кут O, або кут AOB, або кут BOA.
Слово «кут» можна замінити знаком ∠ , записавши кут O так: ∠ O, або ∠ AOB, або
∠ BOA.
Розгорнутий кут — це кут, сторони якого є доповняльними променями.
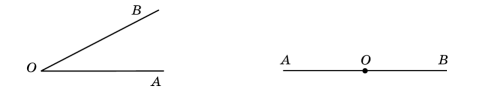
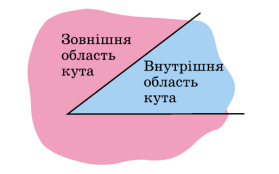 Будь‑який кут ділить площину на дві частини. Якщо кут не є розгорнутим, то одну із частин називають внутрішньою областю кута, а іншу — зовнішньою.
Будь‑який кут ділить площину на дві частини. Якщо кут не є розгорнутим, то одну із частин називають внутрішньою областю кута, а іншу — зовнішньою.
Якщо кут є розгорнутим, то будь‑яку з двох частин, на які він ділить площину, можна вважати внутрішньою областю кута.
Кожний кут має певну градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°.
Основна властивість вимірювання кутів.
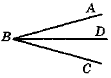
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
Два кути називають рівними, якщо в них однакові градусні міри.
З двох кутів більшим вважають той, градусна міра якого є більшою.
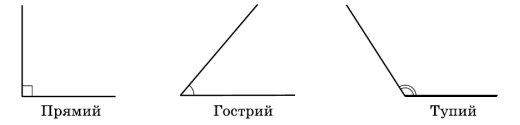
Кут називають прямим, якщо його градусна міра дорівнює 90°, гострим, якщо він менший від прямого, тупим, якщо він більший за прямий, але менший від розгорнутого.
Зверніть увагу!
Від будь-якого променя в одну сторону від нього можна відкласти кут із заданою градусною мірою, меншою від 180, і тільки один.
Треба знати:
|
Кути |
|
|
1. Означення |
|
|
|
Кут ABC ( — внутрішня область кута (частина площини, обмежена променями) |
|
2. Розгорнутий кут |
|
|
|
Промені ВА і ВС — доповняльні, тому |
|
3. Вимірювання кутів |
|
|
а) одиниці вимірювання:
1° (1 градус) — це
1' (1 мінута) — це
1" (1 секунда) — це |
|
|
б) властивості вимірювання |
|
|
|
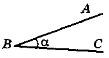
α — градусна міра кута ABC |
|
|
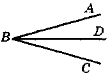
BD — внутрішній промінь кута ABC: |
|
4. Рівні кути |
|
|
|
|
|
|
|
|
5. Бісектриса кута |
|
|
|
BD — внутрішній промінь кута ABC, причому |
Усні вправи
- З точки O проведено два промені: OA і OB. Яка фігура при цьому утворилася?
2. Який з даних кутів гострий, тупий, прямий, розгорнутий:
1) ∠ A = 39°; 2) ∠ B = 90°; 3) ∠ C = 91°; 4) ∠ D = 170°; 5) ∠ M = 180°; 6) ∠ Q = 79°; 7) ∠ P = 1°3′; 8) ∠ F = 173°12′?
3. Обчислити: 1) 7°13′ + 12°49′; 2 ) 52°17′ – 45°27′.
Практичне завдання:
Накресліть кут градусної міри: 1) 30°; 2) 90°; 3) 115°; 4) 75°.
Письмові вправи
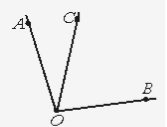 Задача1. Промінь ОС проходить між сторонами кута АОВ, який дорівнює 110°. Які градусні міри кутів АОС і ВОС, якщо кут АОС на 30° менший від кута ВОС ?
Задача1. Промінь ОС проходить між сторонами кута АОВ, який дорівнює 110°. Які градусні міри кутів АОС і ВОС, якщо кут АОС на 30° менший від кута ВОС ?
Розв’язання. Нехай ∠АОС = x°, тоді ∠ВОС = (x + 30)°. Оскільки ∠АОВ = ∠АОС + ∠ВОС, то маємо x + x + 30 = 110. Звідси x = 40. Отже, ∠АОС = 40°, ∠BOC =30° + 40° = 70°.
Відповідь. ∠АОС = 40°, ∠ВОС = 70°
Задача2. Відомо, що ∠АОС = 85°, ∠ВОС = 30°. Чому може дорівнювати кут АОВ?
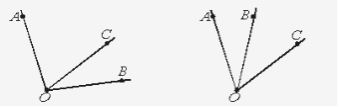
Розв’язання. Кути АОС і ВОС, які мають спільну сторону ОС, можна відкласти від сторони ОС в різні півплощини або в одну півплощину
У першому випадку ∠АОВ = ∠АОС + ∠ВОС = 85° + 30° = 115°.
У другому випадку промінь ОВ лежить між сторонами кута АОС, або промінь ОА лежить між сторонами кута ВОС. Промінь ОА не може проходити між сторонами кута ВОС, бо тоді 30° = ∠ВОА + 85°, що неможливо. Отже, промінь ОВ лежить між сторонами кута АОС.
∠АОС = ∠АОВ + ∠ВОС, ∠ АОВ = ∠АОС –∠ВОС = 85° – 30° = 55°.
Відповідь. 115° або 55°.
Самостійно.
- Промінь OK проходить між сторонами кута BOC. Знайдіть градусну міру кута BOC, якщо ∠ BOK = 38°, ∠ KOC = 42°. Виконайте малюнок.
- Промінь AB ділить кут MAK н а д ва кути. Знай діть градусну міру кута MAK, якщо ∠ MAB = 70°, а кут BAK складає 60 % від кута MAB.
Це цікаво.
Кут у 30° можна побачити на механічному годиннику — це кут між годинною і хвилинною стрілками, наприклад, о 12 годині 5 хвилин.
Кут у 60° можна побачити в рівносторонньому трикутнику — кожен кут такого трикутника має градусну міру 60°.
Кут у 90° можна побачити у приміщеннях, наприклад, кут між стіною і підлогою.
Кут у 120° можна побачити у структурі бджолиних сот.
Кут у 360° проходить годинна стрілка за 1 годину.


про публікацію авторської розробки
Додати розробку