Урок-лекція. Тема модуля: Площі поверхонь тіл обертання.
Навчальний модуль
Об’єми та площі поверхонь
геометричних тіл
Геометрія 11 клас
Підготувала вчитель математики
Яблунського ліцею
Солотвинської селищної ради
Костур Дарія Дмитрівна
Конспект №4
Урок-лекція (2 год)
Тема модуля. Площі поверхонь тіл обертання.
Мета модуля: Ознайомити учнів з поняттям площі поверхні тіла; домогтися засвоєння формул для обчислення площі поверхні циліндра, конуса, сфери та її частин; відпрацювати навички розв’язування задач з даної теми; формувати обчислювальні навички учнів; розвивати творчу діяльність учнів, самостійність; виховувати інтереси до математики; формувати навички колективної та самостійної роботи.
Тип модуля: Змістово-пошуковий.
Обладнання: підручник, міні-підручник, таблиця «Розгортки циліндра, конуса, зрізаного конуса», мультимедійний проектор, моделі круглих тіл, аркуш «Перевір себе».
Хід уроку
І. Перевірка домашнього завдання.
Наприкінці уроку збираються учнівські зошити для перевірки виконання домашнього завдання та ведення зошитів.
ІІ. Актуалізація опорних знань.
За допомогою мультимедійного проектора проектую на дошку вправи і запитання з аркуша «Перевір себе».
- Яка фігура називається кулею, конусом, циліндром?
- Означення вписаної призми, піраміди, многогранника.
- Сформулювати теореми про:
а) переріз кулі площиною;
б) симетрію кулі;
в) дотичну площину до кулі.
- У циліндр, висота якого 10 см, вписано призму. Чому дорівнює площа бічної поверхні призми, якщо периметр її основи дорівнює 16 см?
- У конус вписано правильну чотирикутну піраміду, висота якої дорівнює 6 см, а діагональ основи 16 см. Чому дорівнює:
а) твірна конуса;
б) площа основи конуса?
-
Об’єм кулі дорівнює
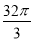 см3. Чому дорівнює радіус кулі?
см3. Чому дорівнює радіус кулі?
- Площа великого круга сфери дорівнює 225π см2. Чому дорівнює діаметр сфери?
ІІІ. Повідомлення теми, мети і завдань уроку.
Перший міні-модуль
- Формування поняття площі поверхні тіла.
- Формула для обчислення площі бічної поверхні циліндра.
- Формула для обчислення повної поверхні циліндра.
- Приклади обчислення площ бічної та повної поверхонь циліндра.
Другий міні-модуль
1. Формула для обчислення площі бічної поверхні конуса.
- Формула для обчислення повної поверхні конуса.
- Формула для обчислення площі бічної поверхні зрізаного конуса.
- Формула для обчислення повної поверхні зрізаного конуса.
- Приклади обчислення площі бічної та повної поверхонь конуса.
Третій міні-модуль
- Формула для обчислення площі сфери.
- Формула для обчислення площі сферичного сегмента.
- Формула для обчислення площі сферичного пояса.
- Приклади обчислення площі сфери та її частин.
IV. Сприйняття, усвідомлення і творче обгрунтування нового матеріалу.
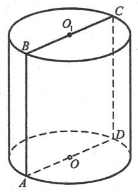
- Формування поняття площі поверхні циліндра (означення площі поверхні циліндра вводиться на основі поняття розгортки циліндра). Робота з таблицею «Розгортка циліндра».
- Площа бічної та повної поверхонь циліндра.
Учні самостійно, працюючи з підручником [6] (§25, с. 186), з’ясовують формули для обчислення площі бічної та повної поверхонь циліндра та розв’язують задачу за готовим малюнком.
Осьовим перерізом циліндра є квадрат зі стороною 8 см. Знайти площу бічної поверхні циліндра
- Площа бічної та повної поверхонь конуса:
- Робота з таблицею «Розгортка конуса»;
- Робота з підручником [6] (§26, с. 192-193);
- Задача 1. Знайти площу повної поверхні конуса, радіус якого дорівнює 2 см, а твірна – 25 см.
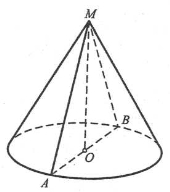
- Задача 2. У зрізаному конусі діагоналі осьового перерізу взаємно перпендикулярні, а твірна l утворює з площею основи кут α. Знайти площу бічної поверхні зрізаного конуса (№1008, §26, підручник [6]).
- Площа сфери.
- Формули для площі сфери та її частин виводяться згідно з §36, підручника [6].
- Задача 1. Площа великого круга кулі дорівнює 25π см2. Знайти площу поверхні кулі.
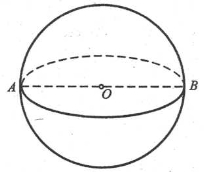
- Задача 2. Радіуси основ кульового пояса дорівнюють 10 см і 12 см, а його висота – 11 см. Обчисліть площу сферичної поверхні кульового пояса, якщо паралельні площини, що перетинають кулю, розташовані по різні боки від центра кулі.
V. Написання короткого конспекту у міні-підручнику
Площі поверхонь тіл обертання
![]() – площа бічної поверхні циліндра, де R – радіус основи, H – висота
– площа бічної поверхні циліндра, де R – радіус основи, H – висота
![]() ,
,
![]() – площа повної поверхні циліндра
– площа повної поверхні циліндра
![]() – площа бічної поверхні конуса, де R – радіус основи конуса, l – довжина твірної
– площа бічної поверхні конуса, де R – радіус основи конуса, l – довжина твірної
![]() – площа бічної поверхні зрізаного конуса, де R1 і R2 – радіуси основ, l – твірна
– площа бічної поверхні зрізаного конуса, де R1 і R2 – радіуси основ, l – твірна
![]() ,
,
![]() – площа повної поверхні конуса
– площа повної поверхні конуса
![]() – площа сфери
– площа сфери
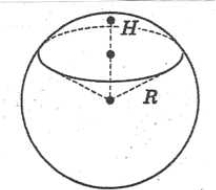
![]() – площа сферичного сегмента, де R – радіус сфери, H – висота сегмента
– площа сферичного сегмента, де R – радіус сфери, H – висота сегмента
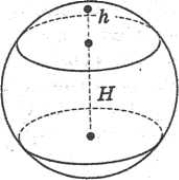
![]() – площа сферичного пояса, де R – радіус кулі, H – висота поясу
– площа сферичного пояса, де R – радіус кулі, H – висота поясу
VІ. Підсумок лекції
VІІ. Домашнє завдання
- Вивчити конспект, п.п. 79-81 підручника [5].
- Розв’язати задачі 36, 38, 42 §8, підручника [5].
- Розв’язати задачі 2.4 (варіант 21), 3.3 (варіант 30) із збірника [4].
Література
- Пєхота О.М. Сучасні освітні технології. – К., А.С.К., 2001.
- Смишляєва В.К. У світі математики. – К.; Рад. шк., 1976. – Випуск 7. – с. 183.
- Пометун О., Пироженко Л. Сучасний урок. – К.: А.С.К., 2003.
- Істер О.С., Глобін І.Є., Панкратова І.Є. Збірник завдань для державної підсумкової атестації з математики. – Київ.: ЦНМЛ, 2011.
- Погорєлов О.В. Геометрія: Стереометрія: Підруч. Для 10-11 кл. серед. шк. К.: Освіта, 1998.
- Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: Стереометрія: Підруч. Для 11 кл загальноосвітніх навчальних закладів. – К.: «Генеза», 2011.
- Погорєлов О.В. Геометрія: Планіметрія: Підручник для 7-9 кл. загальноосвітніх навчальних закладів. – К.: Школяр, 2004.


про публікацію авторської розробки
Додати розробку
