Урок "Логарифмічна функція, її властивості та графік"

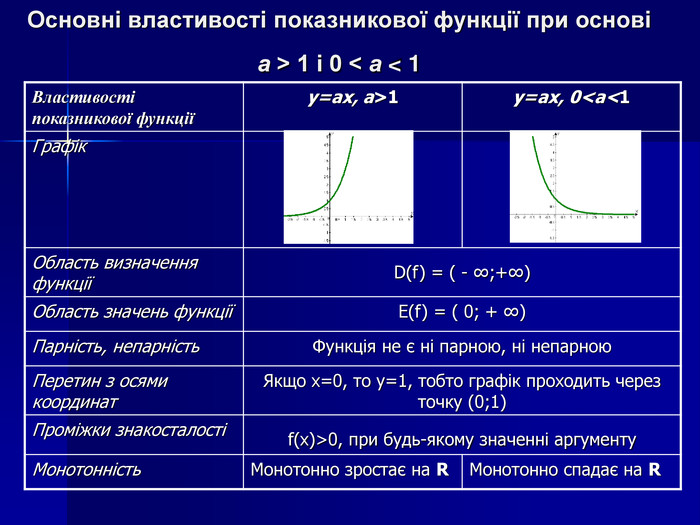
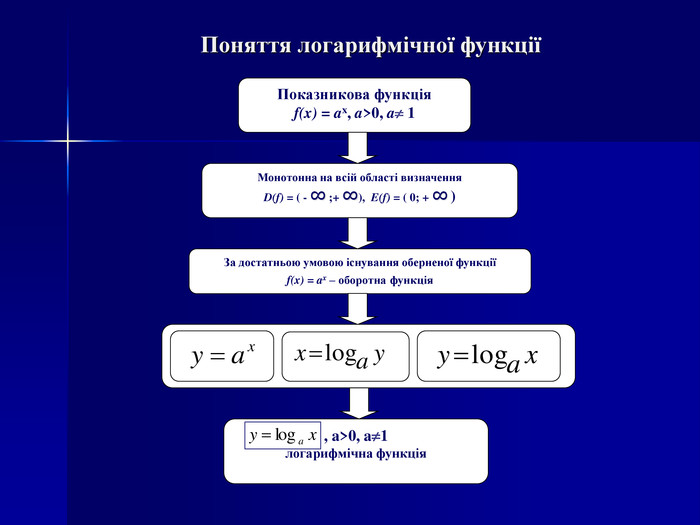
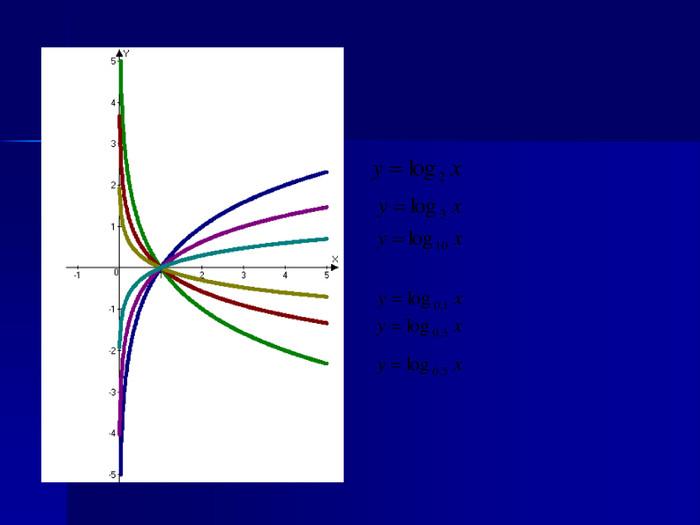
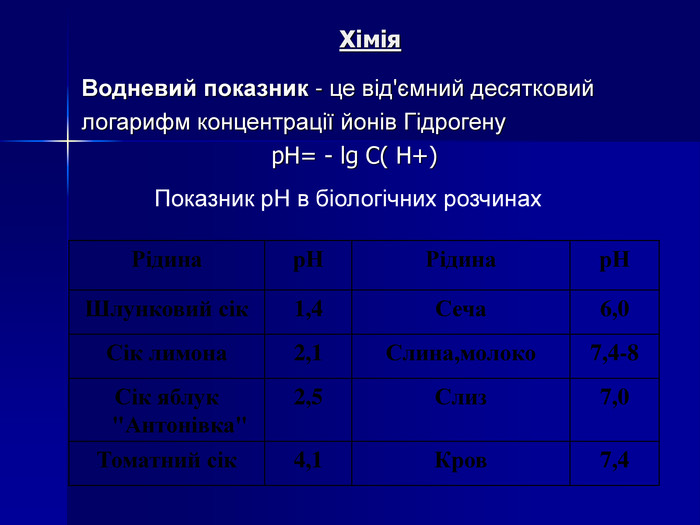
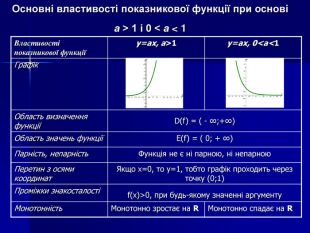
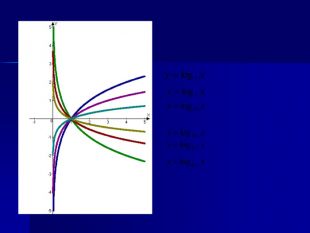
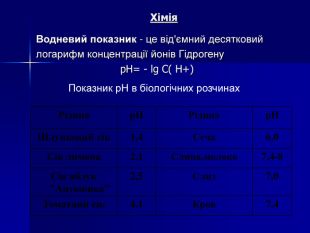
Логарифмічна функція, її властивості та графік

Мета: - ввести поняття логарифмічної функції, формувати вміння будувати графік логарифмічної функції, дослідити її властивості, познайомити учнів з використанням логарифмічної функції при вивченні явищ навколишнього світу; - розвивати творче мислення, математичне мовлення; - виховувати вміння працювати разом, почуття відповідальності, культуру спілкування.

Ми повинні: - розглянути поняття логарифмічної функції; навчитися будувати графік логарифмічної функції; дослідити її властивості; - познайомитися з використанням логарифмічної функції в науці, техніці та природі.

Сьогодні на уроці ми будемо говорити про такі речі:

Залежність змінної у від змінної х називається функцією, якщо кожному значенню х відповідає єдине значення у. 2. Як називаються змінні х та у? Х- незалежна змінна, аргумент; У – залежна змінна, функція. 3. Яку функцію називають оборотною? Функція f, яка має обернену, називається оборотною 1. Що називається функцією? Наведіть приклади Актуалізація опорних знань

4. Назвіть достатню умову існування оберненої функції. Достатньою умовою існування оберненої функції для даної функції є її монотонність,тобто зростання або спадання на всій області визначення. 5. Який існує алгоритм знаходження формули функції, оберненої до даної? а) З’ясувати, чи є функція у = f(x) оборотною на всій області визначення. Якщо ні, то виділити проміжок, на якому функція монотонна; б) виразити х через у; в) поміняти позначення змінних 6. Накресліть схематично графіки функцій у = 3х та у = 0,5х. Сформулюйте основні властивості показникової функції при основі а > 1 і 0 < а < 1.

Монотонно спадає на R Монотонно зростає на R Монотонність f(x)>0, при будь-якому значенні аргументу Проміжки знакосталості Якщо х=0, то у=1, тобто графік проходить через точку (0;1) Перетин з осями координат Функція не є ні парною, ні непарною Парність, непарність E(f) = ( 0; + ∞) Область значень функції D(f) = ( - ∞;+∞) Область визначення функції Графік y=ax, 01 Властивості показникової функції Основні властивості показникової функції при основі а > 1 і 0 < а < 1

а) Область визначення функції f співпадає з областю значень функції , і навпаки, область значень функції f співпадає з областю визначення функції ; б) якщо функція f зростає то і функція  зростає, якщо функція f спадає то і функція  спадає; в) графіки функції , оберненої до функції f, симетричні графіку f відносно прямої у = х 8. Дайте означення логарифма і сформулюйте його основні властивості Логарифмом числа N за основою а (a>0 і a1) називається показник степеня х, до якого треба піднести а, щоб дістати N. 7. Сформулюйте основні властивості взаємно обернених функцій

Монотонна на всій області визначення D(f) = ( - ∞ ;+ ∞), E(f) = ( 0; + ∞ ) За достатньою умовою існування оберненої функції f(x) = ax – оборотна функція Показникова функція f(x) = ax, a>0, a 1 , a>0, a1 логарифмічна функція Поняття логарифмічної функції

Завдання 1. За допомогою програмного педагогічного засобу Advanced Grapher побудувати в одній системі координат графіки функцій: Проблемне питання: Як можна порівнювати логарифми чисел, використовуючи властивості логарифмічної функції? Розгляньте завдання: 1. Порівняйте число а з 1, якщо А. а=1. Б. а<1. В. а>1. Г. а1. 2. Порівняйте числа log25 і log27. А. log25 > log27. Б. log25 < log27. В. log25 = log27. Г. log25  log27. 3. Порівняйте числа log78 і log58. А. log78  log58. Б. log78 > log58. В. log78 = log58.. Г. log78 < log58. 4. Порівняйте числа log4320 і log5500.

Застосування логарифмів та логарифмічної функції в науці, техніці та природі. Математика Логарифм – з грецької означає “логос”- відношення і “аритмос”- число. Його винахід пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі».

Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α. Характерні особливості логарифмічної спіралі: Має нескінченну кількість витків як при розкручуванні так і при скручуванні; Не проходить через свій полюс; Її називають рівнокутною спіраллю; В будь-якій точці спіралі кут між дотичною до неї та її радіус-вектором зберігає постійне значення; При різних перетвореннях (гомотетії, повороті) вона залишається незмінною. Має широке застосування в технічних приладах. Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

Ємність циліндричного конденсатора: Ємність дільниці одиничної довжини двох провідної лінії: Зв’язок між сталою розпаду , середнім часом життя а періодом піврозпаду Т Фізика Робота, яку виконує газ при ізотермічному процесі:

У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю. Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

Показник рН в біологічних розчинах 7,4 Кров 4,1 Томатний сік 7,0 Слиз 2,5 Сік яблук "Антонівка" 7,4-8 Слина,молоко 2,1 Сік лимона 6,0 Сеча 1,4 Шлунковий сік рН Рідина рН Рідина Хімія Водневий показник - це від'ємний десятковий логарифм концентрації йонів Гідрогену рН= - lg С( Н+)

У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (рН≈5), а буряк на нейтральних (рН≈7). Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення рН. Більшість рідких косметичних засобів має рН 5,5. Відповідний вміст у них катіонів Н+ оптимальний для нашої шкіри

Біологія Спіраль є математичним символом співвідношення форми і зростання. Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння , закручує нитки навколо центра по логарифмічним спіралям.

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується.

log2 Nmp= m + Звідси видно, що номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика ( тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса ( тобто дробова частина). Музика Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах.

Яка функція є оберненою до показникової? Яка функція називається логарифмічною? При якій умові логарифмічна функція є зростаючою (спадною)? Де використовується в навколишньому світі логарифмічна функція?

Бажаємо вам успіхів у вивченні математики!!!