Урок математики, 6 клас "Цілі числа. Раціональні числа"

Розробка уроку математики для учнів 6 класу

 «Цілі числа. Раціональні числа»

Тема: Цілі числа. Раціональні числа

Мета: навчальна: узагальнити та систематизувати відомості учнів про види чисел; сформувати поняття цілих чисел, раціональних чисел, показати зв'язок між ними; виробити вміння розпізнавати цілі та раціональні числа;

            розвиваюча: розвивати систематичність, послідовність мислення, культуру математичної мови і записів;

            виховна: виховувати працьовитість, старанність, кмітливість, активність.

Очікувані результати: учні повинні знати, які числа називають цілими, раціональними; вміти розпізнавати ці числа, наводити приклади.

Основні поняття: цілі числа, раціональні числа.

Обладнання: підручник, роздавальні матеріали.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

І. Організаційний етап.

ІІ. Перевірка домашнього завдання.

1. Перевірити виконання домашніх вправ шляхом коментування з місця.

Частина учнів отримує картки з індивідуальними завданнями.

2. Математичний диктант

Визначте, чи є правильним твердження (так∩, ні _).

1. Числа –20 і 20 є протилежними.
2. У кожного числа є безліч протилежних.
3. Число 0 протилежне самому собі.
4. Якщо число а додатне, то протилежне йому – від’ємне.
5. На координатній прямій протилежні числа розташовані по один бік від початку відліку.
6. Якщо m=– (–7), то m=7.

Відповідь. ∩_∩∩_∩

ІІІ. Актуалізація опорних знань учнів.

Фронтальне опитування

1. Які числа називають натуральними? Наведіть приклади.
2. Назвіть найменше натуральне число.
3. Назвіть найбільше натуральне число.
4. Назвіть число, протилежне:

а) найбільшому двоцифровому числу;

б) найменшому двоцифровому числу;

в) найбільшому трицифровому числу;

г) найменшому трицифровому числу.

5.  Наведіть приклади:

а) додатних дробових чисел;

б) від’ємних дробових чисел.

ІV. Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності.

 Назвіть одним словом числа, приведені в кожному з рядів:

а) 35;  208;  2;  1000;  1;  59;

б) 2,5;  ;  ;  0,7;  200,01;  ;

в) –25;  –3,5;  –49;  –100;  –0,6;

г) 35;  9,8;  60;  700;  0,5;  124.

Дійсно, а) – натуральні; б) – дробові; в) – від’ємні; г) – додатні.

А чи можна одним словом назвати числа:

а) –5;  10;  19;  –13;  0;  –203;

б) 29;  –3,6;  ;  ;  0,98;  –207?

Так, бо в першому ряду числа цілі, а в другому – раціональні. Отже, дізнаємося, які числа називають цілими, а які – раціональними.

V. Вивчення нового матеріалу.

 1. Поняття цілого числа. Позначення цілого числа

2. Поняття раціонального числа. Позначення раціонального числа.

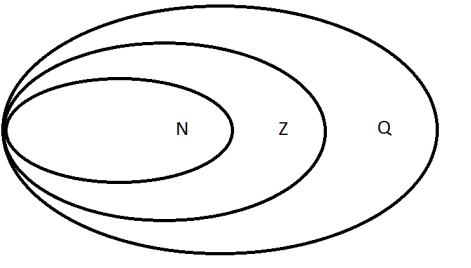
3. Зв’язок між натуральними, цілими і раціональними числами.

 Натуральні числа , протилежні їм числа і число 0 називають цілими числами (Z). Наприклад, –20;  39;  0;  –1002;  45 098 – цілі числа.

Цілі числа (додатні і від’ємні), дробові числа (додатні і від’ємні) та число 0 називають раціональними числами (Q). Наприклад, –35;  2,3;  –0,45;  28;  ;  – раціональні числа.

Раціональні числа

                                Цілі числа                                    Дробові числа

Натуральні                                   0              Додатні дробові          Від’ємні дробові

                           Цілі від’ємні

Колективне виконання завдань під керівництвом вчителя:

1. Наведіть приклади цілих чисел, які не є натуральними.
2. Наведіть приклади раціональних чисел, які не є цілими.
3. За допомогою кругів (діаграми) Ейлера розташуйте числа: –6;  2,5;  0;  4;  ; ; 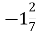12.

Важливо звернути увагу учнів на той момент, що будь-яке з чисел, яке ми можемо дістати шляхом виконання арифметичних дій, є раціональним. Але при цьому може бути натуральним, або цілим, або дробовим.

VІ. Закріплення знань, формування вмінь.

1. Робота з підручником (Мерзляк А. Г. Математика: підруч. для 6 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2014. – 400 с. : іл.)

Вправи: № 872, 877, 878, 879.

2. Додаткові вправи:

1. Запишіть два сусідніх числа, між якими розташоване число: а) 3,6; б) 0,34; в) -5,2; г) 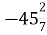; д) –0,21.
2. Знайдіть усі цілі значення х, які задовольняють нерівність:

а) –2,6<х<3,4;         б) –2<х<5.

3.  Робота в парах: Визначте вид числа (якщо відповідь ствердна, поставити у таблиці знак «+», якщо заперечна – «–»).

VІІ. Підбиття підсумків уроку

 Бліц-опитування

Чи правильно, що:

а) будь-яке раціональне число є натуральним;

б)будь-яке ціле число є раціональним;

в) будь-яке раціональне число є цілим;

г) будь-яке натуральне число є раціональним;

д) будь-яке ціле число є натуральним;

будь-яке натуральне число є цілим?

VІІІ. Домашнє завдання

1. Завдання за підручником:§ 4, п. 31, № 873, 878, 880, 888.
2. Додаткове завдання: Доведіть, що значення виразу:

є цілим числом.